北京市丰台区2016-2017学年高考文数二模考试试卷

试卷更新日期：2017-09-13 类型：高考模拟

进入出卷网下载

一、选择题

1. 已知集合A={x|1≤x≤4}，B={x|x＞2}，那么A∪B=（）

A、（2，4） B、（2，4] C、[1，+∞） D、（2，+∞）

查看试题解析
2. 下列函数中，既是偶函数又是（0，+∞）上的增函数的是（）

A、y=x³ B、y=2^|x| C、y=﹣x² D、y=log₃（﹣x）

查看试题解析
3. 某校高一1班、2班分别有10人和8人骑自行车上学，他们每天骑行路程（单位：千米）的茎叶图如图所示：则1班10人每天骑行路程的极差和2班8人每天骑行路程的中位数分别是（）

A、14，9.5 B、9，9 C、9，10 D、14，9

查看试题解析
4. 圆（x+1）²+y²=1的圆心到直线y=x﹣1的距离为（）

A、1 B、 $\frac{\sqrt{2}}{2}$ C、 $\sqrt{2}$ D、2

查看试题解析
5. 执行如图所示的程序框图，若输出的S为4，则输入的x应为（）

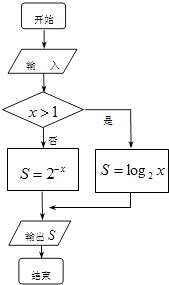A、﹣2 B、16 C、﹣2或8 D、﹣2或16

查看试题解析
6. 已知向量 $\vec{a}$ =（ $\frac{\sqrt{3}}{2}$ ， $\frac{1}{2}$ ）， $\vec{b}$ =（ $\sqrt{3}$ ，﹣1），则 $\vec{a}$ ， $\vec{b}$ 的夹角为（）

A、 $\frac{π}{4}$ B、 $\frac{π}{3}$ C、 $\frac{π}{2}$ D、 $\frac{2 π}{3}$

查看试题解析
7. 一个几何体的三视图如图所示，其中俯视图为正方形，则最长侧棱（不包括底面的棱）的长度为（）

A、2 B、 $\sqrt{6}$ C、 $2 \sqrt{2}$ D、 $2 \sqrt{3}$

查看试题解析
8. 血药浓度（Plasma Concentration）是指药物吸收后在血浆内的总浓度．药物在人体内发挥治疗作用时，该药物的血药浓度应介于最低有效浓度和最低中毒浓度之间．已知成人单次服用1单位某药物后，体内血药浓度及相关信息如图所示：
根据图中提供的信息，下列关于成人使用该药物的说法中，不正确的是（）

A、首次服用该药物1单位约10分钟后，药物发挥治疗作用 B、每次服用该药物1单位，两次服药间隔小于2小时，一定会产生药物中毒 C、每间隔5.5小时服用该药物1单位，可使药物持续发挥治疗作用 D、首次服用该药物1单位3小时后，再次服用该药物1单位，不会发生药物中毒

查看试题解析

二、填空题

9. 双曲线 $\frac{x^{2}}{4} - y^{2} = 1$ 的焦点坐标是．

查看试题解析
10. 已知复数z=（1﹣i）（i﹣2），则|z|= ．

查看试题解析
11. 在△ABC中，角A，B，C对应的边长分别是a，b，c，且 $\sqrt{3} a s i n B = b c o s A$ ，则角A的大小为．

查看试题解析
12. 若实数x，y满足约束条件 ${\begin{matrix} x \geq 0 \\ y \leq x \\ x + y + a \leq 0 \end{matrix}$ 且z=x+3y的最大值为4，则实数a的值为．

查看试题解析
13. 已知函数 $f (x) = {\begin{matrix} - {(x - 1)}^{2} + 2 ， x \leq 1 \\ \frac{1}{x} + 1 ， x > 1. \end{matrix}$ 下列四个命题：
①f（f（1））＞f（3）；
②∃x₀∈（1，+∞）， $f' (x_{0}) = - \frac{1}{3}$ ；
③f（x）的极大值点为x=1；
④∀x₁ ， x₂∈（0，+∞），|f（x₁）﹣f（x₂）|≤1
其中正确的有．（写出所有正确命题的序号）

查看试题解析
14. 在平面直角坐标系xOy中．点M不与点O重合，称射线OM与圆x²+y²=1的交点N为点M的“中心投影点“．
⑴点M（1， $\sqrt{3}$ ）的“中心投影点”为
⑵曲线x² $- \frac{y^{2}}{3} = 1$ 上所有点的“中心投影点”构成的曲线的长度是．

查看试题解析

三、解答题

15. 已知等比数列{a_n}的公比q=2，前3项和是7，等差数列{b_n}满足b₁=3，2b₂=a₂+a₄ ．
（Ⅰ）求数列{a_n}，{b_n}的通项公式；
（Ⅱ）求数列 ${\frac{2}{(2 n - 1) b_{n}}}$ 的前n项和S_n ．

查看试题解析
16. 已知函数f（x）=sinxsin $(\frac{π}{2} - x) + \sqrt{3} c o s^{2}$ x．
（Ⅰ）求f（x）的最小正周期；
（Ⅱ）求f（x）的单调递增区间．

查看试题解析
17. 如图，四棱锥P﹣ABCD中，PD⊥平面PAB，AD∥BC，BC=CD= $\frac{1}{2}$ AD，E，F分别为线段AD，PD的中点．
（Ⅰ）求证：CE∥平面PAB；
（Ⅱ）求证：PD⊥平面CEF；
（Ⅲ）写出三棱锥D﹣CEF与三棱锥P﹣ABD的体积之比．（结论不要求证明）

查看试题解析
18. 某校为研究学生语言学科的学习情况，现对高二200名学生英语和语文某次考试成绩进行抽样分析．将200名学生编号为001，002，…，200，采用系统抽样的方法等距抽取10名学生，将10名学生的两科成绩（单位：分）绘成折线图如下：
（Ⅰ）若第一段抽取的学生编号是006，写出第五段抽取的学生编号；
（Ⅱ）在这两科成绩差超过20分的学生中随机抽取2人进行访谈，求2人成绩均是语文成绩高于英语成绩的概率；
（Ⅲ）根据折线图，比较该校高二年级学生的语文和英语两科成绩，写出你的结论和理由．

查看试题解析
19. 已知椭圆C： $\frac{x^{2}}{4} + \frac{y^{2}}{3} = 1$ ，点P（4，0），过右焦点F作与y轴不垂直的直线l交椭圆C于A，B两点．
（Ⅰ）求椭圆C的离心率；
（Ⅱ）求证：以坐标原点O为圆心与PA相切的圆，必与直线PB相切．

查看试题解析
20. 已知函数 $f (x) = \frac{l n x}{a x}$ （a＞0）．
（Ⅰ）当a=1时，求曲线y=f（x）在点（1，f（1））处的切线方程；
（Ⅱ）若 $f (x) < \frac{1}{\sqrt{x}}$ 恒成立，求a的取值范围；
（Ⅲ）证明：总存在x₀ ，使得当x∈（x₀ ， +∞），恒有f（x）＜1．

查看试题解析