北京市丰台区2016-2017学年高一下学期期末数学考试试卷

试卷更新日期：2017-09-13 类型：期末考试

进入出卷网下载

一、选择题

1. 如果a＞b，那么下列不等式中一定成立的是（）

A、a+c＞b+c B、 $\sqrt{a} > \sqrt{b}$ C、c﹣a＞c﹣b D、a²＞b²

查看试题解析
2. 等比数列{a_n}中，a₂=1，a₄=2，则a₆=（）

A、 $2 \sqrt{2}$ B、4 C、 $4 \sqrt{2}$ D、8

查看试题解析
3. 执行如图所示的程序框图，如果输入的x=2，则输出的y等于（）

A、2 B、4 C、6 D、8

查看试题解析
4. 某几何体的三视图如图所示，其中俯视图是等腰三角形，那么该几何体的体积是（）

A、96 B、128 C、140 D、152

查看试题解析
5. 在△ABC中，角A、B、C所对的边分别为a、b、c，若B=60°，b²=ac，则△ABC一定是（）

A、直角三角形 B、钝角三角形 C、等边三角形 D、等腰直角三角形

查看试题解析
6. 二次函数y=ax²+bx+c（x∈R）的部分对应值如表：
x
﹣3
﹣2
﹣1
0
1
2
3
4
y
﹣6
0
4
6
6
4
0
﹣6
则一元二次不等式ax²+bx+c＞0的解集是（）

A、{x|x＜﹣2，或x＞3} B、{x|x≤﹣2，或x≥3} C、{x|﹣2＜x＜3} D、{x|﹣2≤x≤3}

查看试题解析
7. 在数列{a_n}中，a_n+1=a_n+2，且a₁=1，则 $\frac{1}{a_{1} a_{2}} + \frac{1}{a_{2} a_{3}} + \frac{1}{a_{3} a_{4}} + \dots + \frac{1}{a_{9} a_{10}}$ =（）

A、 $\frac{9}{19}$ B、 $\frac{18}{19}$ C、 $\frac{10}{21}$ D、 $\frac{20}{21}$

查看试题解析
8. 已知各项均为正数的等比数列{a_n}中，如果a₂=1，那么这个数列前3项的和S₃的取值范围是（）

A、（﹣∞，﹣1] B、[1，+∞） C、[2，+∞） D、[3，+∞）

查看试题解析
9. 已知n次多项式 $f_{n} (x) = a_{n} x^{n} + a_{n - 1} x^{n - 1} + \dots + a_{1} x + a_{0}$ ，在求f_n（x₀）值的时候，不同的算法需要进行的运算次数是不同的．例如计算 $x_{0}^{k}$ （k=2，3，4，…，n）的值需要k﹣1次乘法运算，按这种算法进行计算f₃（x₀）的值共需要9次运算（6次乘法运算，3次加法运算）．现按如图所示的框图进行运算，计算f_n（x₀）的值共需要次运算．（）

A、2ⁿ B、2n C、 $\frac{n (n + 1)}{2}$ D、n+1

查看试题解析
10. 如图，在正方体ABCD﹣A₁B₁C₁D₁中，点P在正方体表面运动，如果 $S_{△ A B D_{1}} = S_{△}_{P B D_{1}}$ ，那么这样的点P共有（）

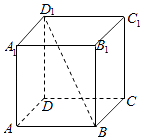A、2个 B、4个 C、6个 D、无数个

查看试题解析

二、填空题

11. 从某企业生产的某种产品中抽取100件样本，测量这些样本的一项质量指标值，由测量结果得如下频数分布表：
质量指标
值分组
[75，85）
[85，95）
[95，105）
[105，115）
[115，125]
频数
6
26
38
22
8
则样本的该项质量指标值落在[105，125]上的频率为．

查看试题解析
12. 函数f（x）=x（2﹣x）（0＜x＜2）的最大值是．

查看试题解析
13. 如图，样本数为9的三组数据，它们的平均数都是5，频率条形图如下，则标准差最大的一组是．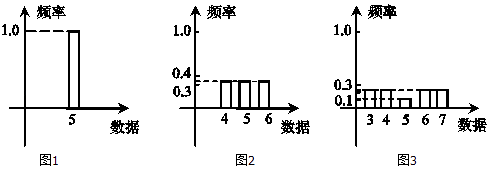

查看试题解析
14. 已知两条不重合的直线a，b和两个不重合的平面α，β，给出下列命题：
①如果a∥α，b⊂α，那么a∥b；
②如果α∥β，b⊂α，那么b∥β；
③如果a⊥α，b⊂α，那么a⊥b；
④如果α⊥β，b⊂α，那么b⊥β．
上述结论中，正确结论的序号是（写出所有正确结论的序号）．

查看试题解析
15. 如图，为了测量河对岸A，B两点之间的距离．观察者找到了一个点C，从C可以观察到点A，B；找到了一个点D，从D可以观察到点A，C；找到了一个点E，从E可以观察到点B，C．并测量得到图中一些数据，其中 $C D = 2 \sqrt{3}$ ，CE=4，∠ACB=60°，∠ACD=∠BCE=90°，∠ADC=60°，∠BEC=45°，则AB ．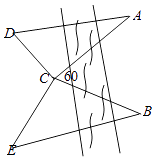

查看试题解析
16. 数列{a_n}满足a₁=1， $a_{n} \cdot a_{n + 1} = 2^{n - 1}$ ，其前n项和为S_n ，则

(1)、a₅=；

(2)、S_2n= ．

查看试题解析

三、解答题

17. 在△ABC中，角A，B，C的对边分别为a，b，c，且 $s i n A = \sqrt{6} s i n C$ ， $c = \sqrt{3}$ ．
（Ⅰ）求a的值；
（Ⅱ）如果 $c o s A = \frac{\sqrt{3}}{3}$ ，求b的值及△ABC的面积．

查看试题解析
18. 某校在“普及环保知识节”后，为了进一步增强环保意识，从本校学生中随机抽取了一批学生参加环保基础知识测试．经统计，这批学生测试的分数全部介于75至100之间．将数据分成以下5组：第1组[75，80），第2组[80，85），第3组[85，90），第4组[90，95），第5组[95，100]，得到如图所示的频率分布直方图．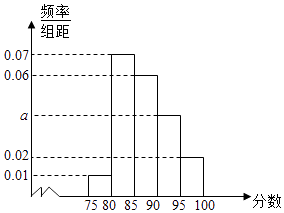
（Ⅰ）求a的值；
（Ⅱ）现采用分层抽样的方法，从第3，4，5组中随机抽取6名学生座谈，求每组抽取的学生人数；
（Ⅲ）假设同一组中的每个数据可用该组区间的中点值代替，试估计随机抽取学生所得测试分数的平均值在第几组（只需写出结论）．

查看试题解析
19. 如图，在四棱锥P﹣ABCD中，底面ABCD为正方形，点E是棱PA的中点，PB=PD，平面BDE⊥平面ABCD．
（Ⅰ）求证：PC∥平面BDE；
（Ⅱ）求证：PC⊥平面ABCD；
（Ⅲ）设PC=λAB，试判断平面PAD⊥平面PAB能否成立；若成立，写出λ的一个值（只需写出结论）．

查看试题解析
20. 设数列{a_n}满足a₁=2， $a_{n + 1} - a_{n} = 2^{n}$ ；数列{b_n}的前n项和为S_n ，且 $S_{n} = \frac{1}{2} (3 n^{2} - n)$ ．
（Ⅰ）求数列{a_n}和{b_n}的通项公式；
（Ⅱ）把数列{a_n}和{b_n}的公共项从小到大排成新数列{c_n}，试写出c₁ ， c₂ ，并证明{c_n}为等比数列．

查看试题解析

x	﹣3	﹣2	﹣1	0	1	2	3	4
y	﹣6	0	4	6	6	4	0	﹣6