2015年广西玉林市、防城港市中考数学真题试卷
试卷更新日期:2016-04-22 类型:中考真卷
一、选择题(每小题3分,共36分,每小题给出的四个选项中只有一个是正确的)
-
1. 的相反数是( )A、 B、 C、-2 D、22. 计算:cos245°+sin245°=( )A、 B、1 C、 D、3. 下列运算中,正确的是( )A、3a+2b=5ab B、2a3+3a2=5a5 C、3a2b﹣3ba2=0 D、5a2﹣4a2=14. 下面角的图示中,能与30°角互补的是( )A、

B、
B、 C、
C、
D、
D、
5.
5.如图是由七个棱长为1的正方体组成的一个几何体,其俯视图的面积是( )
 A、3 B、4 C、5 D、66. 如图,在△ABC中,AB=AC,DE∥BC,则下列结论中不正确的是( )
A、3 B、4 C、5 D、66. 如图,在△ABC中,AB=AC,DE∥BC,则下列结论中不正确的是( )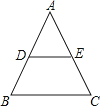 A、AD=AE B、DB=EC C、∠ADE=∠C D、DE=BC7.
A、AD=AE B、DB=EC C、∠ADE=∠C D、DE=BC7.学校抽查了30名学生参加“学雷锋社会实践”活动的次数,并根据数据绘制成了条形统计图,则30名学生参加活动的平均次数是( )
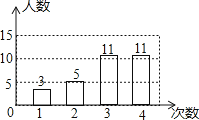 A、2 B、2.8 C、3 D、3.38.
A、2 B、2.8 C、3 D、3.38.如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )
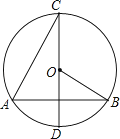 A、AC=AB B、∠C=∠BOD C、∠C=∠B D、∠A=∠BOD9.
A、AC=AB B、∠C=∠BOD C、∠C=∠B D、∠A=∠BOD9.如图,在▱ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2,▱ABCD的周长是14,则DM等于( )
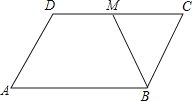 A、1 B、2 C、3 D、410. 某次列车平均提速vkm/h,用相同的时间,列车提速前行驶skm,提速后比提速前多行驶50km.设提速前列车的平均速度为xkm/h,则列方程是( )A、 B、 C、 D、11.
A、1 B、2 C、3 D、410. 某次列车平均提速vkm/h,用相同的时间,列车提速前行驶skm,提速后比提速前多行驶50km.设提速前列车的平均速度为xkm/h,则列方程是( )A、 B、 C、 D、11.如图,ABCD是矩形纸片,翻折∠B,∠D,使AD,BC边与对角线AC重叠,且顶点B,D恰好落在同一点O上,折痕分别是CE,AF,则等于( )
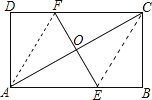 A、 B、2 C、1.5 D、12.
A、 B、2 C、1.5 D、12.如图,反比例函数y=的图象经过二次函数y=ax2+bx图象的顶点(﹣ , m)(m>0),则有( )
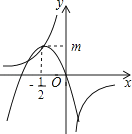 A、a=b+2k B、a=b﹣2k C、k<b<0 D、a<k<0
A、a=b+2k B、a=b﹣2k C、k<b<0 D、a<k<0二、填空题(共6小题,每小题3分,共18分)
-
13. 计算:3﹣(﹣1)= .14. 将太阳半径696000km这个数值用科学记数法表示是 km.15. 分解因式:2x2+4x+2= .
16.某校对学生上学方式进行了一次抽样调查,并根据此次调查结果绘制了一个不完整的扇形统计图,其中“其他”部分所对应的圆心角是36°,则“步行”部分所占百分比是 .
 17.
17.如图,等腰直角△ABC中,AC=BC,∠ACB=90°,点O分斜边AB为BO:OA=1: , 将△BOC绕C点顺时针方向旋转到△AQC的位置,则∠AQC= .
 18. 计算:(﹣3)0×6﹣+|π﹣2|19.
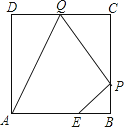
18. 计算:(﹣3)0×6﹣+|π﹣2|19.如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是 .
三、解答题(共8小题,满分66分)
-
20.
解不等式组: , 并把解集在数轴上表示出来.
 21.
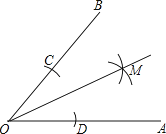
21.根据图中尺规作图的痕迹,先判断得出结论: , 然后证明你的结论(不要求写已知、求证)
 22. 现有三张反面朝上的扑克牌:红桃2、红桃3、黑桃x(1≤x≤13且x为奇数或偶数).把牌洗匀后第一次抽取一张,记好花色和数字后将牌放回,重新洗匀第二次再抽取一张.(1)、求两次抽得相同花色的概率;(2)、当甲选择x为奇数,乙选择x为偶数时,他们两次抽得的数字和是奇数的可能性大小一样吗?请说明理由.(提示:三张扑克牌可以分别简记为红2、红3、黑x)23.
22. 现有三张反面朝上的扑克牌:红桃2、红桃3、黑桃x(1≤x≤13且x为奇数或偶数).把牌洗匀后第一次抽取一张,记好花色和数字后将牌放回,重新洗匀第二次再抽取一张.(1)、求两次抽得相同花色的概率;(2)、当甲选择x为奇数,乙选择x为偶数时,他们两次抽得的数字和是奇数的可能性大小一样吗?请说明理由.(提示:三张扑克牌可以分别简记为红2、红3、黑x)23.如图,在⊙O中,AB是直径,点D是⊙O上一点且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为
 的中点,连接DE,EB.
的中点,连接DE,EB.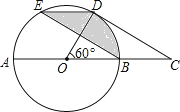 (1)、求证:四边形BCDE是平行四边形;(2)、已知图中阴影部分面积为6π,求⊙O的半径r.24.
(1)、求证:四边形BCDE是平行四边形;(2)、已知图中阴影部分面积为6π,求⊙O的半径r.24.某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
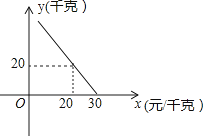 (1)、求y关于x的函数关系式(不要求写出x的取值范围);(2)、应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?25.
(1)、求y关于x的函数关系式(不要求写出x的取值范围);(2)、应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?25.如图,在矩形ABCD中,AB=5,AD=3,点P是AB边上一点(不与A,B重合),连接CP,过点P作PQ⊥CP交AD边于点Q,连接CQ.
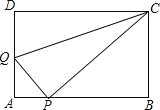 (1)、当△CDQ≌△CPQ时,求AQ的长;(2)、取CQ的中点M,连接MD,MP,若MD⊥MP,求AQ的长.26.
(1)、当△CDQ≌△CPQ时,求AQ的长;(2)、取CQ的中点M,连接MD,MP,若MD⊥MP,求AQ的长.26.已知:一次函数y=﹣2x+10的图象与反比例函数(k>0)的图象相交于A,B两点(A在B的右侧).
 (1)、当A(4,2)时,求反比例函数的解析式及B点的坐标;(2)、在1的条件下,反比例函数图象的另一支上是否存在一点P,使△PAB是以AB为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.(3)、当A(a,﹣2a+10),B(b,﹣2b+10)时,直线OA与此反比例函数图象的另一支交于另一点C,连接BC交y轴于点D.若 , 求△ABC的面积.
(1)、当A(4,2)时,求反比例函数的解析式及B点的坐标;(2)、在1的条件下,反比例函数图象的另一支上是否存在一点P,使△PAB是以AB为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.(3)、当A(a,﹣2a+10),B(b,﹣2b+10)时,直线OA与此反比例函数图象的另一支交于另一点C,连接BC交y轴于点D.若 , 求△ABC的面积.