2015年广西钦州市中考数学真题试卷

试卷更新日期：2016-04-22 类型：中考真卷

进入出卷网下载

一、选择题（每小题3分，共36分，在每小题给出的四个选项中只有一个是符合要求的）

1. 下列图形中，是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 下列实数中，无理数是（　　）

A、-1 B、 $\frac{1}{2}$ C、5 D、 $\sqrt{3}$

查看试题解析
3. 计算（a³）²的结果是（　　）

A、a⁹ B、a⁶ C、a⁵ D、a

查看试题解析
4. 下列几何体中，主视图是圆的是（　　）

A、 B、 C、 D、

查看试题解析
5. 国家统计局4月15日发布数据，初步核算，2015年一季度全国国内生产总值为140667亿元，其中数据140667用科学记数法表示为（　　）

A、1.40667×10⁵ B、1.40667×10⁶ C、14.0667×10⁴ D、0.140667×10⁶

查看试题解析
6.
如图，要使▱ABCD成为菱形，则需添加的一个条件是（　　）

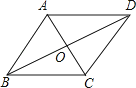A、AC=AD B、BA=BC C、∠ABC=90° D、AC=BD

查看试题解析
7. 用配方法解方程x²+10x+9=0，配方后可得（　　）

A、（x+5）²=16 B、（x+5）²=1 C、（x+10）²=91 D、（x+10）²=109

查看试题解析
8. 在平面直角坐标系中，将点A（x，y）向左平移5个单位长度，再向上平移3个单位长度后与点B（﹣3，2）重合，则点A的坐标是（　　）

A、（2，5） B、（﹣8，5） C、（﹣8，﹣1） D、（2，﹣1）

查看试题解析
9. 对于函数y= $\frac{4}{x}$ ，下列说法错误的是（　　）

A、这个函数的图象位于第一、第三象限 B、这个函数的图象既是轴对称图形又是中心对称图形 C、当x＞0时，y随x的增大而增大 D、当x＜0时，y随x的增大而减小

查看试题解析
10. 在一个不透明的盒子里有2个红球和n个白球，这些球除颜色外其余完全相同，摇匀后随机摸出一个，摸到红球的概率是 $\frac{1}{5}$ ，则n的值为（　　）

A、3 B、5 C、8 D、10

查看试题解析
11.
如图，AD是△ABC的角平分线，则AB：AC等于（　　）

A、BD：CD B、AD：CD C、BC：AD D、BC：AC

查看试题解析
12. 对于任意的正数m、n定义运算※为：m※n= $\{\begin{matrix} \sqrt{m} - \sqrt{n} (m \geq n) \\ \sqrt{m} + \sqrt{n} (m < n) \end{matrix}$ ，计算（3※2）×（8※12）的结果为（　　）

A、2﹣4 $\sqrt{6}$ B、2 C、2 $\sqrt{5}$ D、20

查看试题解析

二、填空题（共6小题，每小题3分，共18分）

13.
如图，直线AB和OC相交于点O，∠AOC=100°，则∠1= 度．

查看试题解析
14. 一组数据3，5，5，4，5，6的众数是．

查看试题解析
15. 一次函数y=kx+b（k≠0）的图象经过A（1，0）和B（0，2）两点，则它的图象不经过第象限．

查看试题解析
16. 当m=2015时，计算： $\frac{m^{2}}{m + 2}$ ﹣ $\frac{4}{m + 2}$ = ．

查看试题解析
17.
如图，在4×4的正方形网格中，每个小正方形的边长均为1，将△AOB绕点O逆时针旋转90°得到△COD，则旋转过程中形成的阴影部分的面积为．

查看试题解析
18.
如图，以O为位似中心，将边长为256的正方形OABC依次作位似变换，经第一次变化后得正方形OA₁B₁C₁ ，其边长OA₁缩小为OA的 $\frac{1}{2}$ ，经第二次变化后得正方形OA₂B₂C₂ ，其边长OA₂缩小为OA₁的 $\frac{1}{2}$ ，经第，三次变化后得正方形OA₃B₃C₃ ，其边长OA₃缩小为OA₂的 $\frac{1}{2}$ ， …，依次规律，经第n次变化后，所得正方形OA_nB_nC_n的边长为正方形OABC边长的倒数，则n= ．

查看试题解析

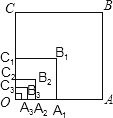
三、解答题（本大题共8题，共66分）

19. 计算：5⁰+|﹣4|﹣2×（﹣3）

查看试题解析
20.
如图，在矩形ABCD中，点E、F分别是边AB、CD的中点．求证：DE=BF．

查看试题解析
21. 抛物线y=x²﹣4x+3与x轴交于A、B两点（点A在点B的左侧），点C是此抛物线的顶点．

(1)、求点A、B、C的坐标；

(2)、点C在反比例函数 $y = \frac{k}{x}$ （k≠0）的图象上，求反比例函数的解析式．

查看试题解析
22. 某体育馆计划从一家体育用品商店一次性购买若干个气排球和篮球（每个气排球的价格都相同，每个篮球的价格都相同）．经洽谈，购买1个气排球和2个篮球共需210元；购买2个气排球和3个篮球共需340元．

(1)、每个气排球和每个篮球的价格各是多少元？

(2)、该体育馆决定从这家体育用品商店一次性购买气排球和篮球共50个，总费用不超过3200元，且购买气排球的个数少于30个，应选择哪种购买方案可使总费用最低？最低费用是多少元？

查看试题解析
23.
某校决定在6月8日“世界海洋日”开展系列海洋知识的宣传活动，活动有A．唱歌、B．舞蹈、C．绘画、D．演讲四项宣传方式．学校围绕“你最喜欢的宣传方式是什么？”在全校学生中进行随机抽样调查（四个选项中必选且只选一项），根据调查统计结果，绘制了如下两种不完整的统计图表：
选项
方式
百分比
A
唱歌
35%
B
舞蹈
a
C
绘画
25%
D
演讲
10%

请结合统计图表，回答下列问题：

(1)、本次抽查的学生共人，a= ，并将条形统计图补充完整；

(2)、如果该校学生有1800人，请你估计该校喜欢“唱歌”这项宣传方式的学生约有多少人？

(3)、学校采用抽签方式让每班在A、B、C、D四项宣传方式中随机抽取两项进行展示，请用树状图或列表法求某班所抽到的两项方式恰好是“唱歌”和“舞蹈”的概率．

查看试题解析
24.
如图，船A、B在东西方向的海岸线MN上，均收到已触礁搁浅的船P的求救信号，已知船P在船A的北偏东60°方向上，在船B的北偏西37°方向上，AP=30海里．

(1)、尺规作图：过点P作AB所在直线的垂线，垂足为E（要求：保留作图痕迹，不写作法）；

(2)、求船P到海岸线MN的距离（即PE的长）；

(3)、若船A、船B分别以20海里/时、15海里/时的速度同时出发，匀速直线前往救援，试通过计算判断哪艘船先到达船P处．（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）

查看试题解析
25.
如图，AB为⊙O的直径，AD为弦，∠DBC=∠A．

(1)、求证：BC是⊙O的切线；

(2)、连接OC，如果OC恰好经过弦BD的中点E，且tanC= $\frac{1}{2}$ ， AD=3，求直径AB的长．

查看试题解析
26.
如图，在平面直角坐标系中，以点B（0，8）为端点的射线BG∥x轴，点A是射线BG上一个动点（点A与点B不重合），在射线AG上取AD=OB，作线段AD的垂直平分线，垂足为E，且与x轴交于点F，过点A作AC⊥OA，交射线EF于点C，连接OC、CD．设点A的横坐标为t．

(1)、用含t的式子表示点E的坐标为；

(2)、当t为何值时，∠OCD=180°？

(3)、当点C与点F不重合时，设△OCF的面积为S，求S与t之间的函数解析式．

查看试题解析

选项	方式	百分比
A	唱歌	35%
B	舞蹈	a
C	绘画	25%
D	演讲	10%