2015年广西柳州市中考数学真题试卷
试卷更新日期：2016-04-22 类型：中考真卷
一、选择题：本大题共12小题，每小题3分，满分36分
-
1.
如图是小李书桌上放的一本书，则这本书的俯视图是（ ）
A、
B、
C、
D、
2.如图，这是某用户银行存折中2012年11月到2013年5月间代扣电费的相关数据，从中可以看出扣缴电费最多的一次达到（ ）
A、147.40元 B、143.17元 C、144.23元 D、136.83元3. 某学校小组5名同学的身高（单位：cm）分别为：147，151，152，156，159，则这组数据的中位数是（ ）A、147 B、151 C、152 D、1564.如图，图中∠α的度数等于（ ）
A、135° B、125° C、115° D、105°5. 下列图象中是反比例函数图象的是（ ）
A、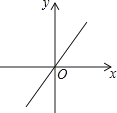
B、
C、
D、
6.如图，BC是⊙O的直径，点A是⊙O上异于B，C的一点，则∠A的度数为（ ）
A、60° B、70° C、80° D、90°7. 小张抛一枚质地均匀的硬币，出现正面朝上的可能性是（ ）A、25% B、50% C、75% D、85%8.如图，点A（﹣2，1）到y轴的距离为（ ）
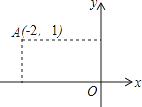A、-2 B、1 C、2 D、9. 在下列单项式中，与2xy是同类项的是（ ）A、2x2y2 B、3y C、xy D、4x10.如图，图中∠1的大小等于（ ）
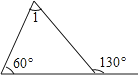A、40° B、50° C、60° D、70°11.如图，二次函数y=ax2+bx+c的图象与x轴相交于（﹣2，0）和（4，0）两点，当函数值y＞0时，自变量x的取值范围是（ ）
A、x＜﹣2 B、﹣2＜x＜4 C、x＞0 D、x＞412.如图，G，E分别是正方形ABCD的边AB，BC的点，且AG=CE，AE⊥EF，AE=EF，现有如下结论：
①BE=GE； ②△AGE≌△ECF； ③∠FCD=45°； ④△GBE∽△ECH，其中，正确的结论有（ ）
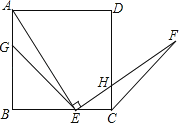A、1个 B、2个 C、3个 D、4个二、填空题（本大题共6小题，每小题3分，满分18分）
-
13. 计算：a×a= ．14.
如图，△ABC≌△DEF，则EF= ．
15. 直线y=2x+1经过点（0，a），则a= ．16.如图，在Rt△ABC中，∠C=90°，AB=13，AC=7，则sinB= ．
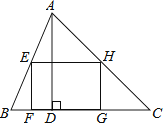
17. 若x=1是一元二次方程x2+2x+m=0的一个根，则m的值为 ．18.如图，矩形EFGH内接于△ABC，且边FG落在BC上．若BC=3，AD=2，EF=EH，那么EH的长为 ．
三、解答题（本大题共8小题，满分66分）
-
19. 计算：+ ．20.
如图，小黄和小陈观察蜗牛爬行，蜗牛在以A为起点沿直线匀速爬向B点的过程中，到达C点时用了6分钟，那么还需要多长时间才能到达B点？
21.如图，在△ABC中，D为AC边的中点，且DB⊥BC，BC=4，CD=5．
(1)、求DB的长；(2)、在△ABC中，求BC边上高的长．22.如图，这是某校初三年级同学们最喜爱的一项课外运动调查结果扇形图，但负责画此图的同学忘记了最喜爱篮球运动的人数．
(1)、请你求出图中的x值；(2)、如果该年级最喜爱跳绳运动的同学有144人，那么这个年级共有多少人？23.如图，在矩形OABC中，OA=3，OC=2，F是AB上的一个动点（F不与A，B重合），过点F的反比例函数（k＞0）的图象与BC边交于点E．
(1)、当F为AB的中点时，求该函数的解析式；(2)、当k为何值时，△EFA的面积最大，最大面积是多少？24.如图，在四边形ABCD中，AD∥BC，∠B=90°，AB=8cm，AD=12cm，BC=18cm，点P从点A出发以2cm/s的速度沿A→D→C运动，点P从点A出发的同时点Q从点C出发，以1cm/s的速度向点B运动，当点P到达点C时，点Q也停止运动．设点P，Q运动的时间为t秒．
(1)、从运动开始，当t取何值时，PQ∥CD？(2)、从运动开始，当t取何值时，△PQC为直角三角形？25.如图，已知四边形ABCD是平行四边形，AD与△ABC的外接圆⊙O恰好相切于点A，边CD与⊙O相交于点E，连接AE，BE．
(1)、求证：AB=AC；(2)、若过点A作AH⊥BE于H，求证：BH=CE+EH．26.如图，已知抛物线y=（x2﹣7x+6）的顶点坐标为M，与x轴相交于A，B两点（点B在点A的右侧），与y轴相交于点C．
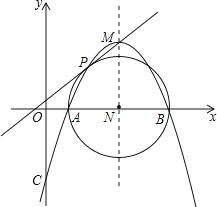(1)、用配方法将抛物线的解析式化为顶点式：y=a（x﹣h）2+k（a≠0），并指出顶点M的坐标；(2)、在抛物线的对称轴上找点R，使得CR+AR的值最小，并求出其最小值和点R的坐标；(3)、以AB为直径作⊙N交抛物线于点P（点P在对称轴的左侧），求证：直线MP是⊙N的切线．