贵州省贵阳市2019-2020学年八年级下学期数学开学试卷
试卷更新日期:2020-04-28 类型:开学考试
一、单选题
-
1. 下列实数中,属于无理数的是( )A、 B、 C、 D、2. 已知一个直角三角形模板三边的平方和为1800,则它的斜边的长为( )A、30 B、80 C、90 D、1203. 如图,在正方形网格中,若点 的坐标分别是 ,则 点的坐标为( )
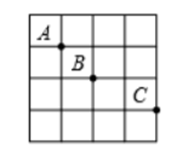 A、 B、 C、 D、4. 我市某一周每天的最高气温统计如下(单位:℃):27,28,29,28,29,30,29.这组数据的众数与中位数分别是( ).A、28,28 B、28,29 C、29,28 D、29,295. 已知点 与点 关于x轴对称,m=( ),n=( ).A、 B、 C、 D、6. 如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=110°,则∠4的度数为( )
A、 B、 C、 D、4. 我市某一周每天的最高气温统计如下(单位:℃):27,28,29,28,29,30,29.这组数据的众数与中位数分别是( ).A、28,28 B、28,29 C、29,28 D、29,295. 已知点 与点 关于x轴对称,m=( ),n=( ).A、 B、 C、 D、6. 如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=110°,则∠4的度数为( )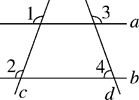 A、70° B、80° C、110° D、100°7. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,那么小巷的宽度为( )
A、70° B、80° C、110° D、100°7. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,那么小巷的宽度为( ) A、0.7米 B、1.5米 C、2.2米 D、2.4米8. 一次函数 的图象可能是( )A、
A、0.7米 B、1.5米 C、2.2米 D、2.4米8. 一次函数 的图象可能是( )A、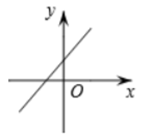 B、
B、 C、
C、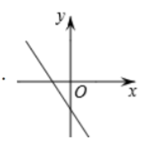 D、
D、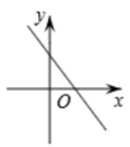 9. 《九章算术》是中国古代数学的重要著作,方程术是它的最高成就,其中记载:今有牛五、羊二,直金十两;牛二、羊五,直金八两。问:牛、羊各直金几何?译文:“假设有 5 头牛、2 只羊,值金 10 两;2 头牛、5 只羊,值金 8 两。问:每头牛、每只羊各值金多少两?” 设每头牛值金 x 两,每只羊值金 y 两,则列方程组错误的是( )A、 B、 C、 D、10. 如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )
9. 《九章算术》是中国古代数学的重要著作,方程术是它的最高成就,其中记载:今有牛五、羊二,直金十两;牛二、羊五,直金八两。问:牛、羊各直金几何?译文:“假设有 5 头牛、2 只羊,值金 10 两;2 头牛、5 只羊,值金 8 两。问:每头牛、每只羊各值金多少两?” 设每头牛值金 x 两,每只羊值金 y 两,则列方程组错误的是( )A、 B、 C、 D、10. 如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )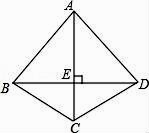 A、AB=AD B、AC平分∠BCD C、AB=BD D、△BEC≌△DEC
A、AB=AD B、AC平分∠BCD C、AB=BD D、△BEC≌△DEC二、填空题
-
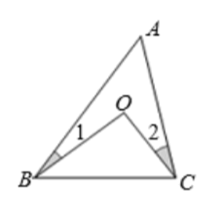
11. 已知:一个正数的两个平方根分别是 和 ,则 的值是.12. 点 在函数 的图象上,则13. 如图,已知 为 内任意一点,且 ,则 .
 14. 如图,直线 与直线 相交于点 ,则方程组 的解是.
14. 如图,直线 与直线 相交于点 ,则方程组 的解是.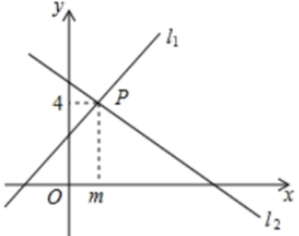 15. 如图,点 是 的平分线 上一点, 于点 .若 ,则点 到 的距离是.
15. 如图,点 是 的平分线 上一点, 于点 .若 ,则点 到 的距离是.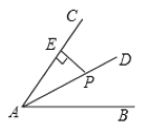
三、解答题
-
16. 计算:(1)、(2)、17. 如图,在四边形 中,点 分别在 和 上,已知 , .求证:
 18. 如图正方形网格中的△ABC , 若小方格边长为1,请你根据所学的知识
18. 如图正方形网格中的△ABC , 若小方格边长为1,请你根据所学的知识 (1)、求△ABC的面积;(2)、判断△ABC是什么形状? 并说明理由.19. 如图, 三个顶点的坐标分别为
(1)、求△ABC的面积;(2)、判断△ABC是什么形状? 并说明理由.19. 如图, 三个顶点的坐标分别为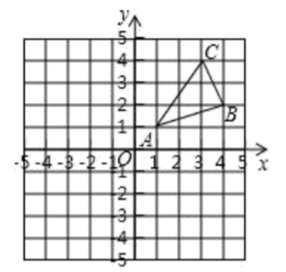 (1)、在图中画出 关于 轴的对称图形 ,并写出点 的坐标;(2)、求 的面积;(3)、在 轴上找出使 的值最小的点 ,并写出点 的坐标.20. 周口市某水果店一周内甲、乙两种水果每天销售情况统计如下:(单位:千克)
(1)、在图中画出 关于 轴的对称图形 ,并写出点 的坐标;(2)、求 的面积;(3)、在 轴上找出使 的值最小的点 ,并写出点 的坐标.20. 周口市某水果店一周内甲、乙两种水果每天销售情况统计如下:(单位:千克)品种 星期
一
二
三
四
五
六
日
甲
乙
(1)、分别求出本周内甲、乙两种水果每天销售量的平均数;21. 甲开车从距离B市100千米的A市出发去B市,乙从同一路线上的C市出发也去往B.市,二人离A市的距离与行驶时间的函数图象如图所示(y代表距离,x代表时间) (1)、C市离A市的距离是千米;(2)、甲的速度是千米∕小时,乙的速度是千米∕小时;(3)、小时,甲追上乙;(4)、试分别写出甲、乙离开A市的距离y(千米)与行驶时间x(时)之间的函数关系式.
(1)、C市离A市的距离是千米;(2)、甲的速度是千米∕小时,乙的速度是千米∕小时;(3)、小时,甲追上乙;(4)、试分别写出甲、乙离开A市的距离y(千米)与行驶时间x(时)之间的函数关系式.