浙江省杭州市拱墅区2020年数学中考模拟试卷(4月)
试卷更新日期:2020-04-28 类型:中考模拟
一、选择题(每小题3分,满分30分)
-
1. ﹣6的绝对值等于( )A、6 B、 C、﹣ D、﹣62. 下列运算正确的是( )A、(a+b)2=a2+b2 B、a3+3a3=4a3 C、(﹣2a2)3=6a6 D、(b+a)(a﹣b)=b2﹣a23. 如图所示,点A是半径为2的⊙O外一点,OA=4,AB是⊙O的切线,B为切点,弦BC∥OA,连接AC,则图中阴影部分的面积为( )
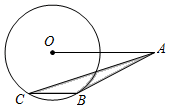 A、2 B、2 C、3 D、4. 某篮球运动员在连续7场比赛中的得分(单位:分)依次为23,22,20,20,20,25,18.则这组数据的众数与中位数分别是( )A、20分,22.5分 B、20分,18分 C、20分,22分 D、20分,20分5. 一个长方形操场的长比宽长70米.根据需要将它扩建,把它的宽增加20米后,它的长就是宽的1.5倍.若设扩建前操场的宽为x米,则下列方程正确的是( )A、x=1.5(x﹣70+20) B、x+70=1.5(x+20) C、x+70=1.5(x﹣20) D、x﹣70=1.5(x+20)6. 如图,已知一组平行线a∥b∥c,被直线m、n所截,交点分别为A,B,C和D,E,F,且AB=1.5,BC=2,DE=1.8,则EF=( )
A、2 B、2 C、3 D、4. 某篮球运动员在连续7场比赛中的得分(单位:分)依次为23,22,20,20,20,25,18.则这组数据的众数与中位数分别是( )A、20分,22.5分 B、20分,18分 C、20分,22分 D、20分,20分5. 一个长方形操场的长比宽长70米.根据需要将它扩建,把它的宽增加20米后,它的长就是宽的1.5倍.若设扩建前操场的宽为x米,则下列方程正确的是( )A、x=1.5(x﹣70+20) B、x+70=1.5(x+20) C、x+70=1.5(x﹣20) D、x﹣70=1.5(x+20)6. 如图,已知一组平行线a∥b∥c,被直线m、n所截,交点分别为A,B,C和D,E,F,且AB=1.5,BC=2,DE=1.8,则EF=( ) A、4.4 B、4 C、3.4 D、2.47. 如图,在△ABC中,∠A=50°,∠1=30°,∠2=40°,∠D的度数是( )
A、4.4 B、4 C、3.4 D、2.47. 如图,在△ABC中,∠A=50°,∠1=30°,∠2=40°,∠D的度数是( ) A、110° B、120° C、130° D、140°8. 一次函数y=ax﹣a(a≠0)的大致图象是( )A、
A、110° B、120° C、130° D、140°8. 一次函数y=ax﹣a(a≠0)的大致图象是( )A、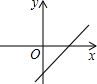 B、
B、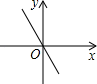 C、
C、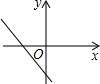 D、
D、 9. 抛物线y=x2+bx+c的对称轴为直线x=1,且经过点(﹣1,0).若关于x的一元二次方程x2+bx+c﹣t=0(t为实数)在﹣1<x<4的范围内有实数根,则t的取值范围是( )A、﹣4≤t<0 B、﹣4≤t<5 C、0<t<5 D、0≤t<510. 如图,△ABC中,AB⊥BC,AB=2CB,以C为圆心,CB为半径作弧交AC于点D,以A为圆心,AD长为半径画弧交AB于点E,则 的值是( )
9. 抛物线y=x2+bx+c的对称轴为直线x=1,且经过点(﹣1,0).若关于x的一元二次方程x2+bx+c﹣t=0(t为实数)在﹣1<x<4的范围内有实数根,则t的取值范围是( )A、﹣4≤t<0 B、﹣4≤t<5 C、0<t<5 D、0≤t<510. 如图,△ABC中,AB⊥BC,AB=2CB,以C为圆心,CB为半径作弧交AC于点D,以A为圆心,AD长为半径画弧交AB于点E,则 的值是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(满分24分,每小题4分)
-
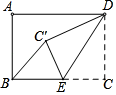
11. 因式分解:9a3b﹣ab=.12. 在不透明纸箱中放有除了标注数字不同其他完全相同的3张卡片,上面分别标注有数字为1、2、3,从中摸出一张,放回搅匀再摸第二张,两次抽得的数字之和为奇数的概率为.13. 方程 的解是 .14. 某扇形的弧长为πcm,面积为3πcm2 , 则该扇形的半径为cm15. 不等式组 有2个整数解,则实数a的取值范围是.16. 矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接DE,把△DCE沿DE折叠,使点C落在点C′处,当△BEC′为直角三角形时,BE的长为.
三、解答题
-
17. 先化简,再求值: ,其中x=﹣ .18. 某校为了在七年级600名学生中顺利开展“四点半”课堂,采用随机抽样的方法,从喜欢乒乓球、跳绳、篮球、绘画四个方面调查了若干名学生,并绘制了条形统计图和扇形统计图,请结合两幅统计图,回答下列问题:
 (1)、这次调查活动中,一共调查了名学生;(2)、“乒乓球”所在扇形的圆心角是度;(3)、请补全条形统计图;(4)、根据本次调查情况,请你估计七年级600名学生中喜欢“乒乓球”的人数有多少?19. 如图,AB是⊙O的直径,点C在圆O上,BE⊥CD垂足为E,CB平分∠ABE,连接BC
(1)、这次调查活动中,一共调查了名学生;(2)、“乒乓球”所在扇形的圆心角是度;(3)、请补全条形统计图;(4)、根据本次调查情况,请你估计七年级600名学生中喜欢“乒乓球”的人数有多少?19. 如图,AB是⊙O的直径,点C在圆O上,BE⊥CD垂足为E,CB平分∠ABE,连接BC (1)、求证:CD为⊙O的切线;(2)、若cos∠CAB= ,CE= ,求AD的长.20. 如图,四边形ABCD是平行四边形,点F在BA的延长线上,连接CF交AD于点E.
(1)、求证:CD为⊙O的切线;(2)、若cos∠CAB= ,CE= ,求AD的长.20. 如图,四边形ABCD是平行四边形,点F在BA的延长线上,连接CF交AD于点E. (1)、求证:△CDE∽△FAE;(2)、当E是AD的中点且BC=2CD时,直接写出图中所有与∠F相等的角.21. 如图,在平面直角坐标系xOy中,一次函数y=k1x+b的图象与反比例函数 (x>0)的图象交于A(m,m+1),B(m+3,m﹣1)两点.
(1)、求证:△CDE∽△FAE;(2)、当E是AD的中点且BC=2CD时,直接写出图中所有与∠F相等的角.21. 如图,在平面直角坐标系xOy中,一次函数y=k1x+b的图象与反比例函数 (x>0)的图象交于A(m,m+1),B(m+3,m﹣1)两点.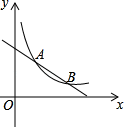 (1)、求m的值;(2)、求出一次函数与反比例函数的表达式;(3)、过点P(a,0)作x轴的垂线,与直线y=k1x+b和函数 (x>0)的图象的交点分别为点M,N,当点M在点N下方时,写出a的取值范围.22. 一个函数y=2x+3与二次函数y=ax2+bx+c的图象交于A(m,5)和B(3,n)两点,且点B是抛物线的顶点.
(1)、求m的值;(2)、求出一次函数与反比例函数的表达式;(3)、过点P(a,0)作x轴的垂线,与直线y=k1x+b和函数 (x>0)的图象的交点分别为点M,N,当点M在点N下方时,写出a的取值范围.22. 一个函数y=2x+3与二次函数y=ax2+bx+c的图象交于A(m,5)和B(3,n)两点,且点B是抛物线的顶点. (1)、求二次函数的解析式;(2)、请在给出的平面直角坐标系中画出一次函数和二次函数的简图(无需列表) , 并根据简图写出:
(1)、求二次函数的解析式;(2)、请在给出的平面直角坐标系中画出一次函数和二次函数的简图(无需列表) , 并根据简图写出:当x满足时,两个函数的值都随x的增大而增大?
当x满足时,二次函数的函数值大于零?
当x满足是,二次函数的值大于一次函数的值?
23. 已知:△ABC与△ABD中,∠CAB=∠DBA=β,且∠ADB+∠ACB=180°.
提出问题:如图1,当∠ADB=∠ACB=90°时,求证:AD=BC;
类比探究:如图2,当∠ADB≠∠ACB时,AD=BC是否还成立?并说明理由.
综合运用:如图3,当β=18°,BC=1,且AB⊥BC时,求AC的长.