山东省新泰市2020年中考数学一模考试试卷
试卷更新日期:2020-04-28 类型:中考模拟
一、选择题(每小题4分,共48分)
-
1. 计算 的值等于( )A、1 B、 C、 D、
-
2. 下列计算正确的是( )A、2x2•2xy=4x3y4 B、3x2y﹣5xy2=﹣2x2y C、x﹣1÷x﹣2=x﹣1 D、(﹣3a﹣2)(﹣3a+2)=9a2﹣4
-
3. 桂林是世界著名的风景旅游城市和历史文化名城,地处南岭山系西南部,广西东北部,行政区域总面积27809平方公里.将27809用科学记数法表示应为()A、 B、 C、 D、
-
4. 已知圆锥的三视图如图所示,则这个圆锥的侧面展开图的面积为( )
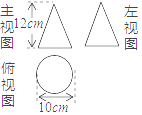 A、60πcm2 B、65πcm2 C、120πcm2 D、130πcm2
A、60πcm2 B、65πcm2 C、120πcm2 D、130πcm2 -
5. 已知抛物线y=x2+2x﹣m﹣1与x轴没有交点,则函数y= 的大致图象是( )A、
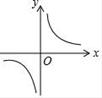 B、
B、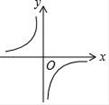 C、
C、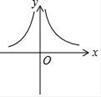 D、
D、
-
6. 在一个不透明的袋子里装有四个小球,球上分别标有6,7,8,9四个数字,这些小球除数字外都相同.甲、乙两人玩“猜数字”游戏,甲先从袋中任意摸出一个小球,将小球上的数字记为m,再由乙猜这个小球上的数字,记为n.如果m,n满足|m﹣n|≤1,那么就称甲、乙两人“心领神会”,则两人“心领神会”的概率是( )A、 B、 C、 D、
-
7. 关于x的方程 的解为非正数,且关于x的不等式组 无解,那么满足条件的所有整数a的和是( )A、﹣19 B、﹣15 C、﹣13 D、﹣9
-
8. 某省加快新旧动能转换,促进企业创新发展.某企业一月份的营业额是1000万元,月平均增长率相同,第一季度的总营业额是3990万元.若设月平均增长率是x,那么可列出的方程是( )A、1000(1+x)2=3990 B、1000+1000(1+x)+1000(1+x)2=3990 C、1000(1+2x)=3990 D、1000+1000(1+x)+1000(1+2x)=3990
-
9. 如图,在菱形 中,点 是 的中点,以 为圆心、 为半径作弧,交 于点 ,连接 .若 , ,则阴影部分的面积为( )
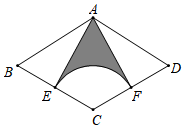 A、 B、 C、 D、
A、 B、 C、 D、 -
10. 下列命题错误的是( )A、平分弦的直径垂直于弦 B、三角形一定有外接圆和内切圆 C、等弧对等弦 D、经过切点且垂直于切线的直线必经过圆心
-
11. 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②3b+2c<0;③4a+c<2b;④m(am+b)+b<a(m≠﹣1),其中结论正确的个数是( )
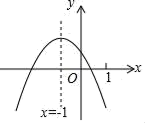 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4 -
12. 如图,在矩形ABCD中,∠ADC的平分线与AB交于E,点F在DE的延长线上,∠BFE=90°,连接AF、CF,CF与AB交于G.有以下结论:①AE=BC②AF=CF③BF2=FG•FC④EG•AE=BG•AB其中正确的个数是( )
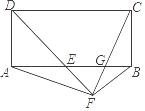 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4
二、填空题(每小题4分,共2分)
-
13. 计算:(π﹣3.14)0+2cos60°= .
-
14. 在Rt△ABC中,∠C=90°,AB=2,BC= ,则sin = .
-
15. 一次函数y=kx﹣3k+1的图象必经过一个定点,该定点的坐标是
-
16. 如图,正方形ABCD的边长为2a,E为BC边的中点, 的圆心分别在边AB、CD上,这两段圆弧在正方形内交于点F,则E、F间的距离为 .
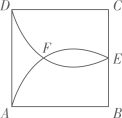
-
17. 已知x , y为实数,y= ,则x﹣6y的值
-
18. 如图,在矩形纸片 中,将 沿 翻折,使点 落在 上的点 处, 为折痕,连接 ;再将 沿 翻折,使点 恰好落在 上的点 处, 为折痕,连接 并延长交 于点 ,若 , ,则线段 的长等于 .
三、解答题
-
19. 先化简,再求值: ,其中a是方程﹣2x2﹣x+3=0的解.
-
20. 如图,一次函数y=ax+b的图象与反比例函数y= 的图象交于C , D两点,与x , y轴交于B , A两点,CE⊥x轴于点E , 且tan∠ABO= ,OB=4,OE=1.
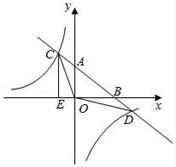 (1)、求一次函数的解析式和反比例函数的解析式(2)、求△OCD的面积;(3)、根据图象直接写出一次函数的值大于反比例函数的值时,自变量x的取值范围.
(1)、求一次函数的解析式和反比例函数的解析式(2)、求△OCD的面积;(3)、根据图象直接写出一次函数的值大于反比例函数的值时,自变量x的取值范围. -
21. 2019年4月23日是第二十四个“世界读书日“.某校组织读书征文比赛活动,评选出一、二、三等奖若干名,并绘成如图所示的条形统计图和扇形统计图(不完整),请你根据图中信息解答下列问题:
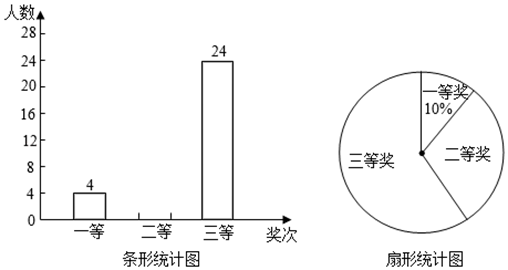 (1)、求本次比赛获奖的总人数,并补全条形统计图;(2)、求扇形统计图中“二等奖”所对应扇形的圆心角度数;(3)、学校从甲、乙、丙、丁4位一等奖获得者中随机抽取2人参加“世界读书日”宣传活动,请用列表法或画树状图的方法,求出恰好抽到甲和乙的概率.
(1)、求本次比赛获奖的总人数,并补全条形统计图;(2)、求扇形统计图中“二等奖”所对应扇形的圆心角度数;(3)、学校从甲、乙、丙、丁4位一等奖获得者中随机抽取2人参加“世界读书日”宣传活动,请用列表法或画树状图的方法,求出恰好抽到甲和乙的概率. -
22. 如图,已知A、B是⊙O上两点,△OAB外角的平分线交⊙O于另一点C,CD⊥AB交AB的延长线于D.
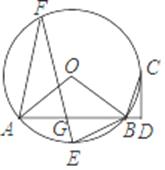 (1)、求证:CD是⊙O的切线;(2)、E为 的中点,F为⊙O上一点,EF交AB于G,若tan∠AFE= ,BE=BG,EG=3 ,求⊙O的半径.
(1)、求证:CD是⊙O的切线;(2)、E为 的中点,F为⊙O上一点,EF交AB于G,若tan∠AFE= ,BE=BG,EG=3 ,求⊙O的半径. -
23. 快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣.已知购买甲型机器人1台,乙型机器人2台,共需14万元;购买甲型机器人2台,乙型机器人3台,共需24万元.
(1)、求甲、乙两种型号的机器人每台的价格各是多少万元;(2)、已知甲型和乙型机器人每台每小时分拣快递分别是1200件和1000件,该公司计划购买这两种型号的机器人共8台,总费用不超过41万元,并且使这8台机器人每小时分拣快递件数总和不少于8300件,则该公司有哪几种购买方案?哪个方案费用最低,最低费用是多少万元?
-
24. 如图1,抛物线y=﹣ [(x﹣2)2+n]与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C , 连结BC .
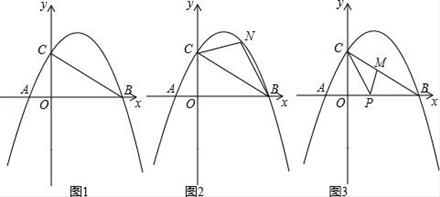 (1)、求m、n的值;(2)、如图2,点N为抛物线上的一动点,且位于直线BC上方,连接CN、BN . 求△NBC面积的最大值;(3)、如图3,点M、P分别为线段BC和线段OB上的动点,连接PM、PC , 是否存在这样的点P , 使△PCM为等腰三角形,△PMB为直角三角形同时成立?若存在,求出点P的坐标;若不存在,请说明理由.
(1)、求m、n的值;(2)、如图2,点N为抛物线上的一动点,且位于直线BC上方,连接CN、BN . 求△NBC面积的最大值;(3)、如图3,点M、P分别为线段BC和线段OB上的动点,连接PM、PC , 是否存在这样的点P , 使△PCM为等腰三角形,△PMB为直角三角形同时成立?若存在,求出点P的坐标;若不存在,请说明理由. -
25. 已知正方形ABCD的对角线AC , BD相交于点O .
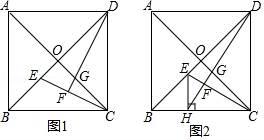 (1)、如图1,E , G分别是OB , OC上的点,CE与DG的延长线相交于点F . 若DF⊥CE , 求证:OE=OG;(2)、如图2,H是BC上的点,过点H作EH⊥BC , 交线段OB于点E , 连结DH交CE于点F , 交OC于点G . 若OE=OG ,
(1)、如图1,E , G分别是OB , OC上的点,CE与DG的延长线相交于点F . 若DF⊥CE , 求证:OE=OG;(2)、如图2,H是BC上的点,过点H作EH⊥BC , 交线段OB于点E , 连结DH交CE于点F , 交OC于点G . 若OE=OG ,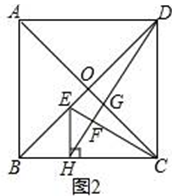
①求证:∠ODG=∠OCE;
②当AB=1时,求HC的长.
