浙江省台州市天台县2020年初中毕业学业模拟考试数学试卷
试卷更新日期:2020-04-28 类型:中考模拟
一、选择题(本大题有10小题,每小题4分,共40分.)
-
1. -2的绝对值是( )A、-2 B、2 C、 D、2. 据悉,2020年台州市重点建设项目总投资67 800 000 000元,数字67 800 000 000用科学记数法可表示为( )A、 B、 C、 D、3. 正五边形是轴对称图形,对称轴有( )A、3条 B、4条 C、5条 D、6条4. 下列图形不可能是长方体展开图的是( )A、
 B、
B、 C、
C、 D、
D、 5. 一枚质地均匀的正方体骰子,其六个面上分别标有数字1,2,3,4,5,6.投掷一次,朝上一面的数字是奇数的概率为( )A、 B、 C、 D、6. 如图,若AB是⊙O的直径,CD是⊙O的弦,∠CDB=58°, 则∠ABC等于( )
5. 一枚质地均匀的正方体骰子,其六个面上分别标有数字1,2,3,4,5,6.投掷一次,朝上一面的数字是奇数的概率为( )A、 B、 C、 D、6. 如图,若AB是⊙O的直径,CD是⊙O的弦,∠CDB=58°, 则∠ABC等于( )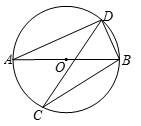 A、32° B、58° C、64° D、42°7. 如图A,B,C,D四个村庄合建一个水站(记为点O),要使铺设到A,B,C,D四个村庄的管道总和最短,即 最小,则水站应建在( )
A、32° B、58° C、64° D、42°7. 如图A,B,C,D四个村庄合建一个水站(记为点O),要使铺设到A,B,C,D四个村庄的管道总和最短,即 最小,则水站应建在( )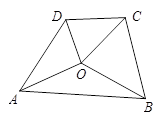 A、AC中点 B、AC与BD交点 C、BD中点 D、A,B,C,D中的任一点8. 如图,抛物线 与直线 交于点 , ,则不等式 的解集为( )
A、AC中点 B、AC与BD交点 C、BD中点 D、A,B,C,D中的任一点8. 如图,抛物线 与直线 交于点 , ,则不等式 的解集为( )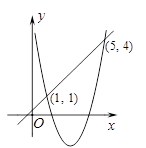 A、 B、 或 C、 D、 或9. 小阳在如图1所示的扇形舞台上沿O-M-N匀速行走,他从点O出发,沿箭头所示的方向经过点M再走到点N,共用时70秒.有一台摄像机选择了一个固定的位置记录了小阳的走路过程,设小阳走路的时间为t(单位:秒),他与摄像机的距离为y(单位:米),表示y与t的函数关系的图象大致如图2,则这个固定位置可能是图1中的( )
A、 B、 或 C、 D、 或9. 小阳在如图1所示的扇形舞台上沿O-M-N匀速行走,他从点O出发,沿箭头所示的方向经过点M再走到点N,共用时70秒.有一台摄像机选择了一个固定的位置记录了小阳的走路过程,设小阳走路的时间为t(单位:秒),他与摄像机的距离为y(单位:米),表示y与t的函数关系的图象大致如图2,则这个固定位置可能是图1中的( )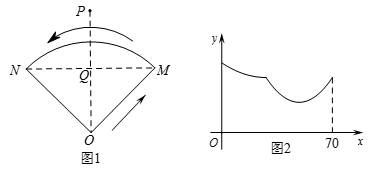 A、点Q B、点P C、点M D、点N10. 甲口袋有x个黑球与若干个白球,乙口袋有若干个黑球与x个白球. 现交换甲乙口袋中的小球,每次交换的数量相等. 交换数次后,下列说法错误的是( )
A、点Q B、点P C、点M D、点N10. 甲口袋有x个黑球与若干个白球,乙口袋有若干个黑球与x个白球. 现交换甲乙口袋中的小球,每次交换的数量相等. 交换数次后,下列说法错误的是( )
A、甲口袋中的黑球数量与乙口袋中的白球数量之和始终为2x个 B、甲口袋中的黑球数量与乙口袋中的白球数量之差可能为1个 C、甲口袋中的黑球数量可能是乙口袋中的白球数量的2倍 D、甲口袋中的黑球数量与乙口袋中的白球数量始终相等二、填空题(本题有6小题,每小题5分,共30分)
-
11. 分解因式: .12. 不等式的解集是 .
13. 把直线 绕原点旋转180 ,所得直线的解析式为.14. 如图,以半圆O的半径OA为直径作一个半圆,点C为小半圆上一点,射线AC交半圆O于点D,已知 的长为3,则 的长为.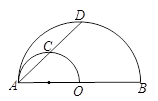 15. “天干地支”纪年法是中国古老的纪年法,由“甲、乙、丙、丁、戊、己、庚、辛、壬、癸”十天干与“子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥”十二地支依次相配组成. 如:甲子、乙丑、丙寅、…. 10年后天干从“甲”重新开始纪年,12年后地支从“子”重新开始纪年,依次下去. 公元2017年对应“丁酉”年,下一次出现“丁酉”年是公元年.16. 如图,点O为直线AB外一定点,点P线段AB上一动点,在直线OP右侧作Rt△OPQ,使得∠OPQ= ,已知AB=3,当点P从点A运动到点B时,点Q运动的路径长是.
15. “天干地支”纪年法是中国古老的纪年法,由“甲、乙、丙、丁、戊、己、庚、辛、壬、癸”十天干与“子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥”十二地支依次相配组成. 如:甲子、乙丑、丙寅、…. 10年后天干从“甲”重新开始纪年,12年后地支从“子”重新开始纪年,依次下去. 公元2017年对应“丁酉”年,下一次出现“丁酉”年是公元年.16. 如图,点O为直线AB外一定点,点P线段AB上一动点,在直线OP右侧作Rt△OPQ,使得∠OPQ= ,已知AB=3,当点P从点A运动到点B时,点Q运动的路径长是.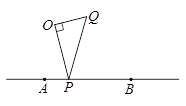
三、解答题(本题有8小题,第17~20题每题8分,第21题10分,第22,23题每题12分,第24题14分,共80分)
-
17.18. 解方程.
19. 人类的血型一般可分为A,B,AB,O型四种.台州中心血站2016年共有8万人无偿献血,血站统计人员由电脑随机选出20人,血型分别是:O,A,O,B,O,A,A,AB,A,O,O,B,AB,B,O,A,O,B,O,A.
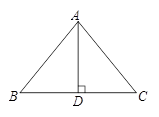
(1)、请设计统计表分类统计这20人各类血型人数;(2)、若平均每位献血者献血200毫升,一年中台州各医院O型血用血量约为6×106毫升,请你估计2016年这8万人所献的O型血是否够用?20. 我们把底角为51°的等腰三角形称为最稳定三角形. 如图,已知△ABC是最稳定三角形, AB=AC,BC=232.8m.求BC边上的高AD的长.(sin51°≈0.8,cos51°≈0.6,tan51°≈1.2,精确到1m)
 21. 水果店张阿姨以每千克2元的价格购进柑桔若干千克,以每千克4元的价格出售,每天可售出50千克,通过调查发现,这种柑桔每千克的售价每降低0.1元,每天可多售出10千克,为保证每天至少售出130千克,张阿姨决定降价销售.(1)、若将柑桔每千克的售价降低x元,则每天的销售量是千克(用含x的代数式表示);(2)、要想销售柑桔每天盈利150元,张阿姨需将每千克的售价降低多少元?22. 如图,四边形ABCD中,∠BAC=∠BDC,
21. 水果店张阿姨以每千克2元的价格购进柑桔若干千克,以每千克4元的价格出售,每天可售出50千克,通过调查发现,这种柑桔每千克的售价每降低0.1元,每天可多售出10千克,为保证每天至少售出130千克,张阿姨决定降价销售.(1)、若将柑桔每千克的售价降低x元,则每天的销售量是千克(用含x的代数式表示);(2)、要想销售柑桔每天盈利150元,张阿姨需将每千克的售价降低多少元?22. 如图,四边形ABCD中,∠BAC=∠BDC,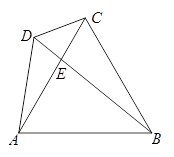 (1)、求证:△ADE∽△CEB;(2)、已知△ABC是等边三角形,求证:
(1)、求证:△ADE∽△CEB;(2)、已知△ABC是等边三角形,求证:① ;
② .
23. 如图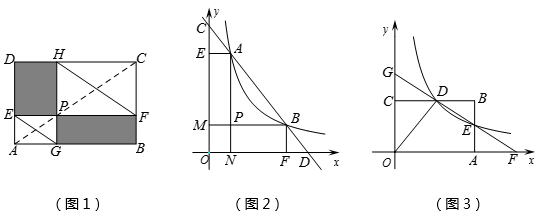 (1)、方法体验:
(1)、方法体验:如图1,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两组对边于点E,F和G,H,容易证明四边形PEDH和四边形PFBG是面积相等的矩形,分别连结EG,FH.
①根据矩形PEDH和矩形PFBG面积相等的关系,那么PE·PH= ▲ .
②求证:EG∥FH.
(2)、方法迁移:如图2,已知直线 分别与x轴,y轴交于D,C两点,
与双曲线 交于A,B两点. 求证:AC=BD.
(3)、知识应用:如图3,反比例函数 (x>0)的图象与矩形ABCO的边BC交于点D,与边AB交于点E, 直线DE与x轴,y轴分别交于点F,G . 若矩形ABCO的面积为10,△ODG与△ODF的面积比为3:5,则k=.
24. 定义:两直角边比为1:2的直角三角形叫做和合三角形.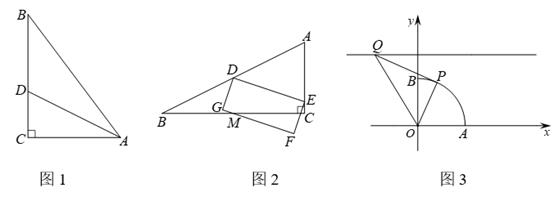 (1)、如图1,△ABC中,∠C= ,AC=3,BC=4,AD平分∠CAB交BC于点D,说明△ACD是和合三角形;(2)、如图2,和合△ABC中,∠C= ,AC= ,点D是边AB中点,点E是边AC上一动点,在直线DE下方构造矩形DEFG,使直线FG始终经过BC中点M,已知△ABC面积为4,求矩形DEFG的面积;(3)、如图3,扇形OAB中,∠AOB= ,OA=2. 以点O为原点,OA,OB所在直线为坐标轴建立平面直角坐标系,点P是 一动点,点Q是直线y=3上一动点,当△OPQ是和 合三角形时,求点P坐标.
(1)、如图1,△ABC中,∠C= ,AC=3,BC=4,AD平分∠CAB交BC于点D,说明△ACD是和合三角形;(2)、如图2,和合△ABC中,∠C= ,AC= ,点D是边AB中点,点E是边AC上一动点,在直线DE下方构造矩形DEFG,使直线FG始终经过BC中点M,已知△ABC面积为4,求矩形DEFG的面积;(3)、如图3,扇形OAB中,∠AOB= ,OA=2. 以点O为原点,OA,OB所在直线为坐标轴建立平面直角坐标系,点P是 一动点,点Q是直线y=3上一动点,当△OPQ是和 合三角形时,求点P坐标.