浙江省温州市2020年数学中考复习卷（一）
试卷更新日期：2020-04-28 类型：中考模拟
一、选择题(本题有10小题，每小题4分，共40分．)
-
1. 计算(-2)+3的结果是（ ）A、-5 B、5 C、-1 D、12. 在太阳系八大行星中，地球与火星是相邻的两颗行星，它们之间的距离约为55 000 000公里，其中数据55 000 000用科学记数法表示为（ ）A、0.55×108 B、5.5×107 C、55×106 D、5.5×1063. 下列几何体的主视图与左视图不相同的是（ ）A、
B、
C、
D、
4. 一个不透明的盒子中装有1个白球，3个红球和6个黄球，这些球除颜色外，没有其他区别，现从这个盒子中随机摸出一个球，摸到红球的概率为（ ）A、 B、 C、 D、5. 图书管理员在整理阅览室的课外书籍时，将其中甲、乙、丙三类书籍的有关数据制成如图所示不完整的统计图，已知甲类书有30本，则丙类书的本数是（ ）
A、90 B、144 C、200 D、806. 不等式组 的解集在数轴上表示正确的是（ ）A、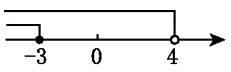
B、
C、
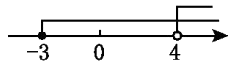D、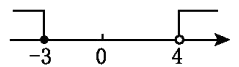
7. 如图，热气球的探测器显示，从热气球A处看一栋楼顶部B处的仰角度数为α，看这栋楼底部C处的俯角度数为β，热气球A处与楼的水平距离为100m，则这栋楼的高度表示为（ ）
A、100(tanα+tanβ)m B、100(sinα+sinβ)m C、 D、8. 已知抛物线y=ax2+bx+c(a<0)过A(-1，1)，B(3，1)，C(-2，y1)，D(2，y2)四点，则y1与y2的大小关系是（ ）A、y1>y2 B、y1=y2 C、y1<y2 D、不能确定9. 如图，A，B是反比例函数y= (x>0)的图象上的两点，过A点作AC⊥x轴，交OB于D点，垂足为C。若△ADO的面积为1，D为OB的中点，则k的值为（ ）
A、 B、 C、3 D、410. 用线段EG，FH将正方形ABCD按如图1所示的方式分割成4个全等的四边形，且AE=BF=CG=DH，tan∠HFC=2，再将这四个四边形按如图2所示的方式拼成一个大正方形IJKL，若设正方形ABCD的面积为S1 ， 正方形IJKL的面积为S2。小四边形MNPQ的面积为8，则 的值为（ ）
A、 B、 C、 D、二、填空题(本题有6小题，每小题5分，共30分)
-
11. 分解因式a²-2a=。12. 若扇形的圆心角为120°，半径为3，则该扇形的面积为 。13. 一组数据：6、3、4、x、7，它们的平均数是5，则这组数据的中位数是。14. 小王的月工资由固定工资与浮动工资两部分组成，固定工资每月2000元，浮动工资逐月增长，每月增长的百分率相同，已知他1月份浮动工资为1000元，3月份的月工资为3440元，则小王2月份的月工资为元。15. 如图，在矩形ABCD中，AB=5，BC=8，在AB的右侧有一点E，且AE=AB，BE=BC，则CE=。
16. 工人师傅在修葺一人字架屋顶BAC时需要加固，计划焊接三根钢条AD，DE，FG。在如图所示的△ABC中，AB=AC=10，BC=12，AD⊥BC于点D，点E，F，G分别是AB，BD，AC上的点，连接DE，GF，交于点H，GF与AD交于点M，当H为FM的中点，BF∶CF=1∶5，AG：AE=5：7时，△AGM的面积为。
三、解答题(本题有8小题，共80分)
-
17. 计算(1)、计算：20200- +|1- |+2sin60°(2)、先化简，再求值 ，其中x= +1。18. 如图，在△ABC与△DCB中，AC与BD交于点E，且∠A=∠D，AB=DC。
(1)、求证：△ABE≌△DCE；(2)、当∠AEB=50°时，求∠EBC的度数。19. 为了解某中学学生课余生活情况，对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计，现从该校随机抽取n名学生作为样本，采用问卷调查的方式收集数据（参与问卷调查的每名学生只能选择其中一项），并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图，由图中提供的信息，解答下列问题：
(1)、补全条形统计图；(2)、若该校共有学生2400名，试估计该校喜爱看电视的学生人数．(3)、若调查到喜爱体育活动的4名学生中有3名男生和1名女生，现从这4名学生中任意抽取2名，求恰好抽到2名男生的概率．20. 图1，图2是两张形状、大小完全相同的8×10方格纸，方格纸中的每个小正方形的边长均为1，点A，B，C均位于格点处，请按要求画出格点四边形(四边形各顶点都在格点上)。
(1)、在图1中画出一个以点A，B，C，P为顶点的格点四边形，且为中心对称图形。(2)、在图2中画出一个以点A，B，C，Q为顶点的格点四边形，AC平分∠BCQ，且有两个内角为90°。21. 如图，已知AB是⊙O的直径，点C在⊙O上，CD是⊙Ｏ的切线，AD⊥CD于点D。E是AB延长线上一点，CE交⊙O于点F，连结OC，AC。
(1)、求证：AC平分∠DAO．(2)、若∠DAO=105°，∠E=30°。①求∠OCE的度数。
②若⊙O的半径为 ，求线段EF的长。
22. 如图，在平面直角坐标系中，抛物线y=ax²-4ax交x轴于点A，直线y= x+3与x轴交于点B，与y轴交于点C，与抛物线交于点D，E(点D在点E的右侧)。
(1)、求点A，B，C的坐标。(2)、当点D为BC的中点时，求a的值。(3)、若设抛物线的顶点为点M，点M关于直线BC的对称点为N， 当点N落在△BOC的内部时，求a的取值范围。23. “创科集团”会议室内的一个长为6米、宽为4米的矩形ABCD墙面需要进行装饰，设计图案如图所示，将矩形ABCD墙面分割成3个区域，中间“十”字形区域甲的宽度均为1米，四个角为四个全等的直角三角形，△AEF，△BGH，△CMN，△DPQ为区域乙，剩下部分为区域丙，其中AE=BG=CN=DP，设EG=HM=NP=FQ=x(米)(1≤x≤3)
(1)、当x=2时，求区域乙的面积；(2)、求区域丙的面积的最大值；(3)、为了图案富有美感，设置区域乙与区域丙的面积之比为1：4，在区域甲、区域乙、区域丙分别嵌贴甲、乙、丙三种不同的装饰板，这三种装饰板每平方米的单价分别为a(百元)，b(百元)，c(百元)(a，b，c均为整数，且6<a<10)，若a+b+c=20，整个墙面嵌贴共花费了150(百元)，求三种装饰板每平方米的单价。24. 如图，在矩形ABCD中，AB=8，AD=6，P为射线AB上一个动点，过P作PF⊥AC，垂足为F，交CD于点G，连接CP与BF交于点H，过点C，P，F作⊙O。
(1)、当AP=5时，求证：∠CPB=∠FBC。(2)、当点P在线段AB上时，若△FCH的面积等于△PBH面积的4倍，求DG的长。(3)、当⊙O与△ADC的其中一边相切时，求所有满足条件的AP的长。(4)、当H将线段CP分成1：4的两部分时，求AP的长(直接写出结果)。