浙江省衢州市2019-2020学年七年级下学期数学期中考试试卷

试卷更新日期：2020-04-28 类型：期中考试

进入出卷网下载

一、选择题(本题有8小题，每小题3分，共24分)

1. 下列运算正确的是（）

A、3x-2x=x B、3x+2x=5x² C、3x·2x=6x D、3x÷2x= $\frac{2}{3}$

查看试题解析
2. 如图，将三角板的直角顶点C(∠ACB=90°)放在直尺的一边上，若∠2=65°，则∠1的度数是（）

A、15° B、25° C、35° D、65°

查看试题解析
3. 下列多项式相乘不能用平方差公式计算的是（）

A、(2x-3y)(3y-2x) B、(-2x+3y)(-2x-3y) C、(x-2y)(2y+x) D、(x+3y)(x-3y)

查看试题解析
4. 已知x^m=2，xⁿ=3，则x^3m-2n的值为（）

A、 $\frac{9}{8}$ B、 $\frac{8}{9}$ C、-1 D、1

查看试题解析
5. 下面是投影屏上出示的抢答题，需要回答横线上符号代表的内容。
已知：如图，∠BEC=∠B+∠C

求证：AB∥CD

证明：延长BE交※于点F，

则∠BEC=180°-∠FEC=◎+∠C

又∠BEC=∠B+∠C，得∠B=▲

故AB∥CD(@相等，两直线平行)

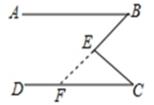
则回答正确的是（）

A、◎代表∠FEC B、@代表同位角 C、▲代表∠EFC D、※代表AB

查看试题解析
6. 若方程组 ${\begin{cases} 3 x - 2 y = 2 k - 3 \\ 2 x + 7 y = 3 k - 2 \end{cases}$ 的解满足x+y=2020，则k等于（）

A、2018 B、2019 C、2020 D、2021

查看试题解析
7. 《九章算术》是我国古代数学的经典著作，书中有一个问题：“今有黄金九枚，白银一十一枚，称之重适等．交易其一，金轻十三两．问金、银一枚各重几何？”．意思是：甲袋中装有黄金9枚(每枚黄金重量相同)，乙袋中装有白银11枚(每枚白银重量相同)，称量两袋发现其重量相等．两袋互相交换1枚后，甲袋比乙袋轻了13两(袋子重量忽略不计)。问黄金、白银每枚各重多少两？设每枚黄金重x两，每枚白银重y两，则根据题意可建立方程组为（）

A、 ${\begin{cases} 11 x = 9 y \\ (8 x + y) + (10 y + x) = 13 \end{cases}$ B、 ${\begin{cases} 11 x = 9 y \\ (10 y + x) - (8 x + y) = 13 \end{cases}$ C、 ${\begin{cases} 9 x = 11 y \\ (10 y + x) - (8 x + y) = 13 \end{cases}$ D、 ${\begin{cases} 9 x = 11 y \\ (8 x + y) + (10 y + x) = 13 \end{cases}$

查看试题解析
8. 如图，在长方形ABCD中放入一个边长为8的大正方形ALMN和两个边长为6的小正方形(正方形DEFG和正方形HIJK)。3个阴影部分的面积满足2S₃+S₁-S₂=2，则长方形ABCD的面积为（）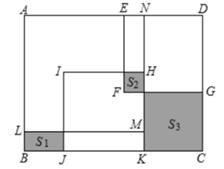

A、100 B、96 C、90 D、86

查看试题解析

二、填空题(本题共有8小题，每小题3分，共24分)

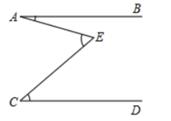
9. 计算：-(-2a²)²=。

查看试题解析
10. 如图，AB∥CD，若∠A=20°，∠E=67°，则∠C的度数为。

查看试题解析
11. 如果实数x，y满足方程组 ${\begin{cases} 2 x - y = 1 \\ x + y = 2 \end{cases}$ ，那么(-x+2y)²⁰²⁰=。

查看试题解析
12. 如图，把一张长方形纸片ABCD沿EF折叠，若∠EFG=52°，则∠AEG的度数是。

查看试题解析
13. 已知实数a、b满足a-b=3，ab=2，则a²+b²的值为。

查看试题解析

14. 某学校组织国学知识竞赛，共设置了20道选择题，各题分值相同，每题必答，下表记录了3个参赛者的得分情况。若参赛者D得了82分，则他答对了道题。

参赛者	答对题数	答错题数	得分
A	20	0	100
B	19	1	94
C	14	6	64

查看试题解析

15. 如图，用边长为2m+3的正方形纸片剪出一个边长为m+3的正方形之后，剩余部分可剪拼成一个长方形，若拼成的长方形一边长为m，则这个长方形的周长为。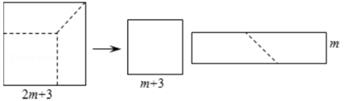

查看试题解析
16. 阅读材料后解决问题：
小明遇到下面一个问题：计算(2+1)(2²+1)(2⁴+1)(2⁸+1)。

经过观察，小明发现如果将原式进行适当的变形后可以出现特殊的结构，进而可以应用平方差公式解决问题，具体解法如下：

(2+1)(2²+1)(2⁴+1)(2⁸+1)=(2-1)(2+1)(2²+1)(2⁴+1)(2⁸+1)=(2²-1)(2²+1)(2⁴+1)(2⁸+1)=(2⁴-1)(2⁴+1)(2⁸+1)=(2⁸-1)(2⁸+1)=2¹⁶-1

请你仿照小明解决问题的方法，尝试计算：(6+1)(6²+1)(6⁴+1)(6⁸+1)=。

查看试题解析

三、解答题(本题共有7小题，第17~19小题每小题6分，第20~22小题每小题8分，第23小题10分，共52分。)

17. 将一副三角尺按如图所示方式放置，然后过点C作CF平分∠DCE，交DE于点F。

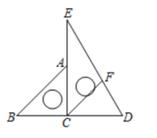(1)、CF与AB平行吗？试说明理由。

(2)、求∠EFC的度数。

查看试题解析
18. 解方程组：

(1)、 ${\begin{cases} 4 x + 3 y = 5 \\ x - 2 y = 4 \end{cases}$

(2)、 ${\begin{cases} \frac{x - 1}{6} - \frac{2 - y}{3} = 1 \\ 2 x + y = 13 \end{cases}$

查看试题解析
19. 化简：

(1)、-12x²y³÷(-3xy²)·( $- \frac{1}{3}$ xy)

(2)、(2x+y)(2x-y)-(2x-y)²

查看试题解析
20. 如图，CD∥AB，点O在AB上，OE平分∠BOD，OF⊥OE，∠D=110°。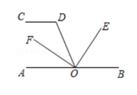

(1)、求∠DOE的度数。

(2)、OF平分∠AOD吗？请说明理由。

查看试题解析
21. 定义新运算 $|\begin{matrix} a & b \\ c & d \end{matrix}|$ =ad+3b-2c，如 $|\begin{matrix} 1 & 5 \\ 3 & 7 \end{matrix}|$ =1×7+3×5-2×3=7+15-6=16。

(1)、计算 $|\begin{matrix} 2 & 3 \\ - 1 & 4 \end{matrix}|$ 的值。

(2)、化简： $|\begin{matrix} x + y & 7 x y - x^{2} \\ 2 x y - 3 x^{2} + 1 & - 3 x - y \end{matrix}|$ 。

查看试题解析
22. 春天来了，衢江河畔，鸟语花香，柳条摇曳。为给衢州市民提供更好的休闲锻炼环境，决定对衢江沿河步行道修建改造。据了解我市步行道改造工程路线约12千米，若该任务由甲、乙两工程队先后接力完成，甲工程队每天修建0.04千米，乙工程队每天修建0.02千米，则两工程队共需修建500天，求甲、乙两工程队分别修建步行道多少千米。
根据题意，小刚同学列出了一个不完整的方程组 ${\begin{cases} x + y = ... \\ 0.04 x + 0.02 y = ... \end{cases}$

(1)、根据小刚同学所列的方程组，请你分别指出未知数x，y表示的意义。x表示；y表示。

(2)、小红同学的做法是：“设甲工程队修建步行道a千米，乙工程队修建步行道b千米”。请你利用小红同学设的未知数解决问题。

查看试题解析
23. 【阅读材料】
我们知道，图形也是一种重要的数学语言，它直观形象，能有效地表现一些代数中的数量关系，而运用代数思想也能巧妙地解决一些图形问题。
在一次数学活动课上，张老师准备了若干张如图1所示的甲、乙、丙三种纸片，其中甲种纸片是边长为x的正方形，乙种纸片是边长为y的正方形，丙种纸片是长为y，宽为x的长方形，并用甲种纸片一张，乙种纸片一张，丙种纸片两张拼成了如图2所示的一个大正方形。

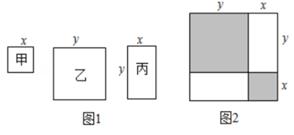(1)、【理解应用】观察图2，用两种不同方式表示阴影部分的面积可得到一个等式，请你直接写出这个等式。

(2)、【拓展升华】利用(1)中的等式解决下列问题：
①已知a²+b²=10，a+b=6，求ab的值。
②已知(2021-c)(c-2019)=2020，求(2021-c)²+(c-2019)²的值。

查看试题解析