山东省济南市章丘区2020年中考数学一模考试试卷
试卷更新日期:2020-04-28 类型:中考模拟
一、选择题
-
1. 下列四个数中,2020 的相反数是( )A、 B、- C、2020 D、- 20202. 下列几何体中,主视图与俯视图不相同的是( )A、
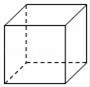 B、
B、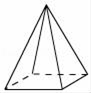 C、
C、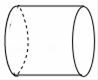 D、
D、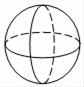 3. 2020年我国爆发“新冠肺炎”疫情,在党中央的坚强领导下,全国上下,众志成城,抗击疫情,截止2020年2月20号,累计确诊70637例,把数70637用科学记数法表示为( )A、7.0637×104 B、7.0637×105 C、7.0637×103 D、0.70637×1054. 如图,直线a,b被直线c所截,若a∥b,∠1=40°,∠2=70°,则∠3=( )
3. 2020年我国爆发“新冠肺炎”疫情,在党中央的坚强领导下,全国上下,众志成城,抗击疫情,截止2020年2月20号,累计确诊70637例,把数70637用科学记数法表示为( )A、7.0637×104 B、7.0637×105 C、7.0637×103 D、0.70637×1054. 如图,直线a,b被直线c所截,若a∥b,∠1=40°,∠2=70°,则∠3=( )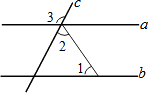 A、70° B、100° C、110° D、120°5. 下表是某校乐团的年龄分布,其中一个数据被遮盖了,下面说法正确的是( )
A、70° B、100° C、110° D、120°5. 下表是某校乐团的年龄分布,其中一个数据被遮盖了,下面说法正确的是( )年龄
13
14
15
16
频数
5
7
13
A、中位数可能是14 B、中位数可能是14.5 C、平均数可能是14 D、众数可能是166. 下列图形中,是中心对称图形的是( )A、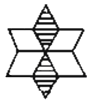 B、
B、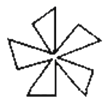 C、
C、 D、
D、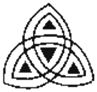 7. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为弧BD,则图中阴影部分的面积是( )
7. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为弧BD,则图中阴影部分的面积是( ) A、 B、 C、 - D、8. 抛物线y=ax2+bx+c的图象如图所示,那么一次函数y=bx+b2﹣4ac与反比例函数y= 在同一坐标系内的图象大致是( )
A、 B、 C、 - D、8. 抛物线y=ax2+bx+c的图象如图所示,那么一次函数y=bx+b2﹣4ac与反比例函数y= 在同一坐标系内的图象大致是( )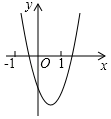 A、
A、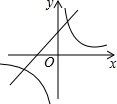 B、
B、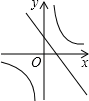 C、
C、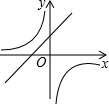 D、
D、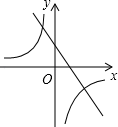 9. 如图所示,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β,已知大桥主架顶端离水面的高CD=a , 则此时测量点与大桥主架的水平距离AB为( )
9. 如图所示,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β,已知大桥主架顶端离水面的高CD=a , 则此时测量点与大桥主架的水平距离AB为( )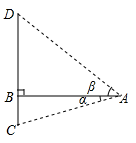 A、asinα+asinβ B、atanα+atanβ C、 D、10. 如图,已知点A(-6,0),B(2,0),点C在直线 上,则使△ABC是直角三角形的点C的个数为( )
A、asinα+asinβ B、atanα+atanβ C、 D、10. 如图,已知点A(-6,0),B(2,0),点C在直线 上,则使△ABC是直角三角形的点C的个数为( )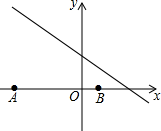 A、1 B、2 C、3 D、411. 如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是
A、1 B、2 C、3 D、411. 如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )
 A、 B、 C、5 D、612. 已知函数y= ,当a≤x≤b时,﹣ ≤y≤ ,则b﹣a的最大值为( )A、1 B、 +1 C、 D、
A、 B、 C、5 D、612. 已知函数y= ,当a≤x≤b时,﹣ ≤y≤ ,则b﹣a的最大值为( )A、1 B、 +1 C、 D、二、填空题
-
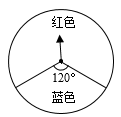
13. 分解因式:2x3﹣8x= .14. 等于数时,代数式 的值比 的值的 倍小 .15. 如图,一个可以自由转动的转盘,任意转动转盘一次,当转盘停止时,指针落在红色区域的概率为 .
 16. 如图,正五边形ABCDE内接于⊙O,F是CD弧的中点,则∠CBF的度数为 .
16. 如图,正五边形ABCDE内接于⊙O,F是CD弧的中点,则∠CBF的度数为 . 17. 甲、乙两人分别从两地同时出发登山,甲、乙两人距山脚的竖直高度y(米)与登山时间x(分)之间的图象如图所示,若甲的速度一直保持不变,乙出发2分钟后加速登山,且速度是甲速度的4倍,那么他们出发分钟时,乙追上了甲.
17. 甲、乙两人分别从两地同时出发登山,甲、乙两人距山脚的竖直高度y(米)与登山时间x(分)之间的图象如图所示,若甲的速度一直保持不变,乙出发2分钟后加速登山,且速度是甲速度的4倍,那么他们出发分钟时,乙追上了甲. 18. 如图,在矩形ABCD中, ,点E为对角线BD的中点,点F在CB的延长线上,且 ,连接EF,过点E作 交BA的延长线于点G,连接GF并延长交DB的延长线于点H,则 .
18. 如图,在矩形ABCD中, ,点E为对角线BD的中点,点F在CB的延长线上,且 ,连接EF,过点E作 交BA的延长线于点G,连接GF并延长交DB的延长线于点H,则 .
三、计算题
-
19. 计算: ﹣20180﹣|﹣5|+( )﹣2﹣2cos60°20. 解不等式组: ,把它的解集在数轴上表示出来,并写出其整数解.
四、综合题
-
21. 如图,矩形ABCD中,对角线AC、BD交于点O , 以AD、OD为邻边作平行四边形ADOE , 连接BE . 求证:四边形AOBE为菱形.
 22. 某种型号油电混合动力汽车,从A地到B地燃油行驶需纯燃油费用76元,从A地到B地用电行驶需纯用电费用26元,已知每行驶1千米,纯燃油费用比纯用电费用多0.5元.(1)、求每行驶1千米纯用电的费用;(2)、若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元,则至少需用电行驶多少千米?23. 如图,△ABC内接于⊙O , AB为⊙O的直径,过点A作⊙O的切线交BC的延长线于点E , 在弦BC上取一点F , 使AF=AE , 连接AF并延长交⊙O于点D .
22. 某种型号油电混合动力汽车,从A地到B地燃油行驶需纯燃油费用76元,从A地到B地用电行驶需纯用电费用26元,已知每行驶1千米,纯燃油费用比纯用电费用多0.5元.(1)、求每行驶1千米纯用电的费用;(2)、若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元,则至少需用电行驶多少千米?23. 如图,△ABC内接于⊙O , AB为⊙O的直径,过点A作⊙O的切线交BC的延长线于点E , 在弦BC上取一点F , 使AF=AE , 连接AF并延长交⊙O于点D . (1)、求证:∠B=∠CAD;(2)、若CE=2,∠B=30°,求AD的长.24. 为了提高中学生身体素质,学校开设了A:篮球、B:足球、C:跳绳、D:羽毛球四种体育活动,为了解学生对这四种体育活动的喜欢情况,在全校随机抽取若干名学生进行问卷调查(每个被调查的对象必须选择而且只能在四种体育活动中选择一种),将数据进行整理并绘制成以下两幅统计图(未画完整)
(1)、求证:∠B=∠CAD;(2)、若CE=2,∠B=30°,求AD的长.24. 为了提高中学生身体素质,学校开设了A:篮球、B:足球、C:跳绳、D:羽毛球四种体育活动,为了解学生对这四种体育活动的喜欢情况,在全校随机抽取若干名学生进行问卷调查(每个被调查的对象必须选择而且只能在四种体育活动中选择一种),将数据进行整理并绘制成以下两幅统计图(未画完整)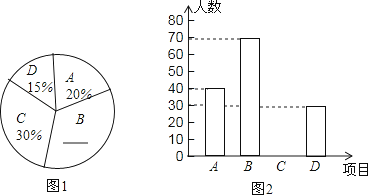 (1)、这次调查中,一共调查了 名学生。
(1)、这次调查中,一共调查了 名学生。
(2)、请补全两幅统计图。
(3)、若有3名喜欢跳绳的学生,1名喜欢足球的学生组队外出参加一次联谊活动,欲从中选出2人担任组长(不分正副),求一人是喜欢跳绳、一人是喜欢足球的学生的概率。
25. 在如图平面直角坐标系中,矩形OABC的顶点B的坐标为(4,2),OA、OC分别落在x轴和y轴上,OB是矩形的对角线.将△OAB绕点O逆时针旋转,使点B落在y轴上,得到△ODE , OD与CB相交于点F , 反比例函数y= (x>0)的图象经过点F , 交AB于点G .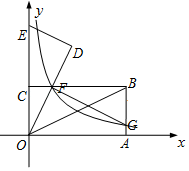 (1)、求k的值和点G的坐标;(2)、连接FG , 则图中是否存在与△BFG相似的三角形?若存在,请把它们一一找出来,并选其中一种进行证明;若不存在,请说明理由;(3)、在线段OA上存在这样的点P , 使得△PFG是等腰三角形.请直接写出点P的坐标.26. 如图,在正方形ABCD中,M、N分别是射线CB和射线DC上的动点,且始终∠MAN=45°.
(1)、求k的值和点G的坐标;(2)、连接FG , 则图中是否存在与△BFG相似的三角形?若存在,请把它们一一找出来,并选其中一种进行证明;若不存在,请说明理由;(3)、在线段OA上存在这样的点P , 使得△PFG是等腰三角形.请直接写出点P的坐标.26. 如图,在正方形ABCD中,M、N分别是射线CB和射线DC上的动点,且始终∠MAN=45°.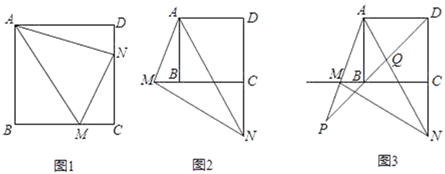 (1)、如图1,当点M、N分别在线段BC、DC上时,请直接写出线段BM、MN、DN之间的数量关系;(2)、如图2,当点M、N分别在CB、DC的延长线上时,(1)中的结论是否仍然成立,若成立,给予证明,若不成立,写出正确的结论,并证明;(3)、如图3,当点M、N分别在CB、DC的延长线上时,若CN=CD=6,设BD与AM的延长线交于点P,交AN于Q,直接写出AQ、AP的长.27. 如图1,在平面直角坐标系中,抛物线y=﹣ x2+ x+ 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D.
(1)、如图1,当点M、N分别在线段BC、DC上时,请直接写出线段BM、MN、DN之间的数量关系;(2)、如图2,当点M、N分别在CB、DC的延长线上时,(1)中的结论是否仍然成立,若成立,给予证明,若不成立,写出正确的结论,并证明;(3)、如图3,当点M、N分别在CB、DC的延长线上时,若CN=CD=6,设BD与AM的延长线交于点P,交AN于Q,直接写出AQ、AP的长.27. 如图1,在平面直角坐标系中,抛物线y=﹣ x2+ x+ 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D. (1)、求直线BC的解析式;(2)、如图2,点P为直线BC上方抛物线上一点,连接PB、PC.当△PBC的面积最大时,在线段BC上找一点E(不与B、C重合),使PE+ BE的值最小,求点P的坐标和PE+ BE的最小值;(3)、如图3,点G是线段CB的中点,将抛物线y=﹣ x2+ x+ 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为F.在抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为直角三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
(1)、求直线BC的解析式;(2)、如图2,点P为直线BC上方抛物线上一点,连接PB、PC.当△PBC的面积最大时,在线段BC上找一点E(不与B、C重合),使PE+ BE的值最小,求点P的坐标和PE+ BE的最小值;(3)、如图3,点G是线段CB的中点,将抛物线y=﹣ x2+ x+ 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为F.在抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为直角三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.