浙江省丽水市2019-2020学年七年级下学期数学期中考试试卷
试卷更新日期：2020-04-28 类型：期中考试
一、选择题(本题有10小题，每小题3分，共30分)
-
1. 如图，与∠1是同位角的是（ ）
A、∠3 B、∠2 C、∠4 D、∠52. 随着微电子制造技术的不断进步，电子元件的尺寸大幅度缩小，在芯片上某种电子元件大约只占0.000 000 65mm²，将0.000 000 65用科学记数法表示为（ ）A、6.5×10-6 B、6.5×10-7 C、65×10-8 D、0.65×10-73. 下列计算正确的是（ ）A、a·a2=a2 B、(a³)²=a5 C、(2a²)3=6a5 D、-2a+3a=a4. 下列选项是二元一次方程的是（ ）A、x+y2=2 B、 =0 C、x- =1 D、x+ y5. 如图所示，a∥b且∠4=110°，则∠1的度数是（ ）
A、20° B、70° C、80° D、110°6. 下列各式从左到右因式分解正确的是（ ）A、2x-6y+2=2(x-3y) B、x²-2x+1=x(x-2)+1 C、x²-4=(x-2)² D、x³-x=x(x+1)(x-1)7. 下列结论错误的是（ ）A、垂直于同一直线的两条直线互相平行 B、两直线平行，同旁内角互补 C、过直线外一点有且只有一条直线与这条直线平行 D、同一平面内，不相交的两条直线叫做平行线8. 如图，将边长为5cm的等边△ABC沿边BC向右平移4cm得到△A'B'C'，则四边形ABC'A'的周长为（ ）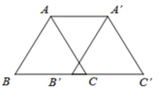
A、28cm B、25cm C、23cm D、21cm9. 若关于x、y的二元一次方程3x-y=7，2x+3y=1，y=-kx-9有公共解，则k的值是（ ）A、-3 B、 C、2 D、-410. 若3x=2，9y=7，则3x+2y的值为（ ）A、 B、 C、14 D、二、填空题(本题有6小题，每小题3分，共18分)
-
11. 因式分解：3x-x²=。12. 写出一个解为 的二元一次方程组：。13. 若4x2-mx+1是完全平方式，则m的值是。14. 如图，把一块直角三角板的直角顶点放在直尺的一边上，如果∠2=58°，那么∠1的度数是。
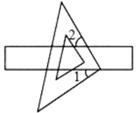15. 若a-b=8，ab=-9，则a²+b²= 。16. 一个长方形的面积为(12ab²-9a²b)，若一边长为3ab，则它的另一边长为。三、解答题(本题有8小题，共52分。)
-
17. 如图，已知∠1=∠2，∠5=140°，求∠3的度数。
解：∵∠1=∠4，（ ▲ ）
又∵∠1=∠2，
∴∠2=∠4，
∴ ▲ ∥ ▲ ， （ ▲ ）
∴∠3+∠ ▲ =180°，（ ▲）
又∵∠5=140°，
∴∠3=▲ °。
18.(1)、计算：(-1)2020+( )-3+32(2)、化简：(x-3)²-(x+3)(x-3)19. 解方程组：(1)、(2)、20. 先化简，再求值：当|x-2|+(y+1)²=0时，求[(3x+2y)(3x-2y)+(2y+x)(2y-3x)]÷4x的值。21. 在如图所示的方格纸中，每个方格都是边长为1个单位长度的小正方形，点A，B，C，D是方格中的格点(即方格中横、纵线的交点)。在方格纸内按要求进行下列作图并计算：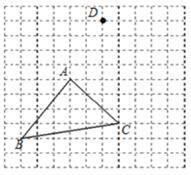
(1)、①过点D作出BC的平行线DE，使DE=BC；②将△ABC先向上平移4个单位长度，再向右平移4个单位长度得到△A1B1C1(其中A，B，C的对应点分别为A1 ， B1 ， C1) ，画出平移后的△A1B1C1；
(2)、求△A1DE的面积。22. 利用完全平方公式进行因式分解，解答下列问题：(1)、因式分解：x²-4x+4= 。(2)、填空：①当x=-2时，代数式x²+4x+4=；②当x=时，代数式x2-6x+9=0。
③代数式x²+8x+20的最小值是 。
(3)、拓展与应用：求代数式a²+b²-6a+8b+28的最小值。23. 某商场计划用56000元从厂家购进60台新型电子产品，已知该厂家生产甲乙、丙三种不同型号的电子产品，设甲、乙型设备应各买入x，y台，其中每台的价格、销售获利如下表：甲型
乙型
丙型
价格(元/台)
1000
800
500
销售获利(元/台)
260
190
120
(1)、购买丙型设备台(用含x，y的代数式表示)；(2)、若商场同时购进三种不同型号的电子产品(每种型号至少有一台)，恰好用了56000元，则商场有哪几种购进方案？(3)、在第(2)题的基础上，为了使销售时获利最多，应选择哪种购进方案？此时获利为多少？24. 如图1是一个长为2a、宽为2b的长方形，沿图中虚线用剪刀剪成四块完全一样的小长方形，然后按图2的形状拼成一个正方形。
(1)、图2中的阴影部分的正方形的边长是。(2)、请用两种不同的方法表示图2中阴影部分的面积，并写出下列三个代数式：(a+b)²，(a-b)²，ab之间的等量关系；(3)、利用(2)中的结论计算：x-y=2，xy= ，求x+y的值；(4)、根据(2)中的结论，直接写出m+ 和m- 之间的关系；若m²-4m+1=0，分别求出m+ 和(m- )2的值。