浙江省丽水市2019-2020学年八年级下学期数学期中考试试卷
试卷更新日期:2020-04-28 类型:期中考试
一、选择题(本题有10小题,每小题3分,共30分)
-
1. 使二次根式 有意义的x的取值范围是( )A、x> B、x≥- C、x≤3 D、x≤-32. 在下列图形中,中心对称图形有( )
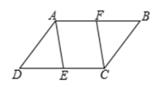
 A、4个 B、3个 C、2个 D、1个3. 当多边形的边数增加1时,它的内角和会( )A、增加160° B、增加180° C、增加270° D、增加360°4. 在 ABCD中,∠A:∠B:∠C=3∶6∶3,∠D的度数( )A、90° B、67.5° C、112.5° D、120°5. 将方程x(x-2)=x+3化成一般形式后,二次项系数和常数项分别为( )A、-3,3 B、-1,-3 C、1,3 D、1,-36. 若一个正方形的面积是18,则它的边长是( )A、9 B、4.5 C、3 D、27. 已知三角形两边的长分别是8和6,第三边的长是一元二次方程x²-16x+60=0的一个实数根,则该三角形的面积是( )A、24或2 B、24 C、8 D、24或88. 如图,在 ABCD中,AB=4,BC=6,BC边上的高AE=2,则DC边上的高AF的长是( )
A、4个 B、3个 C、2个 D、1个3. 当多边形的边数增加1时,它的内角和会( )A、增加160° B、增加180° C、增加270° D、增加360°4. 在 ABCD中,∠A:∠B:∠C=3∶6∶3,∠D的度数( )A、90° B、67.5° C、112.5° D、120°5. 将方程x(x-2)=x+3化成一般形式后,二次项系数和常数项分别为( )A、-3,3 B、-1,-3 C、1,3 D、1,-36. 若一个正方形的面积是18,则它的边长是( )A、9 B、4.5 C、3 D、27. 已知三角形两边的长分别是8和6,第三边的长是一元二次方程x²-16x+60=0的一个实数根,则该三角形的面积是( )A、24或2 B、24 C、8 D、24或88. 如图,在 ABCD中,AB=4,BC=6,BC边上的高AE=2,则DC边上的高AF的长是( ) A、2 B、3 C、4 D、59. 如图,在正方形ABCD内,有两条线段MN、EF,M、N、E、F分别在边AB、CD、AD、BC上,小明认为:若MN=EF,则MN⊥EF。小亮认为:若MN上EF,则MN=EF。你认为( )
A、2 B、3 C、4 D、59. 如图,在正方形ABCD内,有两条线段MN、EF,M、N、E、F分别在边AB、CD、AD、BC上,小明认为:若MN=EF,则MN⊥EF。小亮认为:若MN上EF,则MN=EF。你认为( )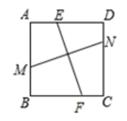 A、两人都对 B、仅小明对 C、仅小亮对 D、两人都不对10. 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+ ,其中正确的序号是( )
A、两人都对 B、仅小明对 C、仅小亮对 D、两人都不对10. 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+ ,其中正确的序号是( )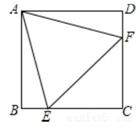 A、①②④ B、①② C、②③④ D、①③④
A、①②④ B、①② C、②③④ D、①③④二、填空题(本题有6小题,每小题2分,共12分)
-
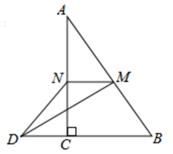
11. =。12. 一个多边形的每一个外角都是40°,则这个多边形是边形。13. 已知关于x的方程x²+2x+2a-1=0的一个根是1,则a=。14. 已知菱形ABCD的一条对角线的长为4,边AB的长是x2-5x+6=0的一个根,则菱形ABCD的周长为。15. 如图,在三角形ABC中,∠ACB=90°,M,N分别是AB、AC的中点,延长BC至点D,使CD= BD,连结DM、DN、MN。若AB=5,则DN=。
 16. 如图,把含45°,30°角的两块直角三角板放置在同一平面内,若AB∥CD,AB=CD= ,则以A,B,C,D为顶点的四边形的面积是。
16. 如图,把含45°,30°角的两块直角三角板放置在同一平面内,若AB∥CD,AB=CD= ,则以A,B,C,D为顶点的四边形的面积是。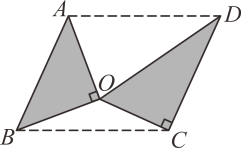
三、解答题(本题有8小题,共58分,各小题都必须写出解答过程)
-
17. 计算:(1)、(2)、(3)、18. 选择适当的方法解下列方程:(1)、x2-4x=0(2)、x²-6x=-8(3)、(x-2)(x-3)=1(4)、(x-3)²=9-x²19. 如图,已知E,F分别是 ABCD的边CD,AB上的点,且DE=BF。求证:AE∥CF。
 20. 2020年拟继续举办丽水市中学生汉字听写、诗词诵写大赛.经过初赛、复赛,选出了两个代表队参加市内7月份的决赛.两个队各选出的5名选手的复赛成绩如图所示。
20. 2020年拟继续举办丽水市中学生汉字听写、诗词诵写大赛.经过初赛、复赛,选出了两个代表队参加市内7月份的决赛.两个队各选出的5名选手的复赛成绩如图所示。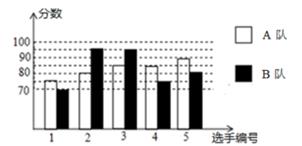 (1)、根据图示补全下表;
(1)、根据图示补全下表;平均数(分)
中位数(分)
众数(分)
A队
83
85
B队
95
(2)、结合两队成绩的平均数和中位数,分析哪个队的复赛成绩较好;(3)、计算两队成绩的方差,并判断哪一个代表队选手成绩较为稳定。21. 如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处。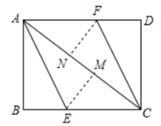 (1)、求证:四边形AECF是平行四边形;(2)、若AB=6,AC=10,求四边形AECF的面积及AE与CF之间的距离。22. 为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子的售价不能超过进价的200%。(1)、请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元。(2)、定价为多少时每天的利润最大?最大利润是多少?23. 如图,四边形ACDE是证明勾股定理时用到的一个图形,a,b,c是全等的Rt△ABC和Rt△BED的边长,易知AE= c,这时我们把关于x的形如ax²+ cx+b=0的一元二次方程称为“勾系一元二次方程”。请解决下列问题:
(1)、求证:四边形AECF是平行四边形;(2)、若AB=6,AC=10,求四边形AECF的面积及AE与CF之间的距离。22. 为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子的售价不能超过进价的200%。(1)、请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元。(2)、定价为多少时每天的利润最大?最大利润是多少?23. 如图,四边形ACDE是证明勾股定理时用到的一个图形,a,b,c是全等的Rt△ABC和Rt△BED的边长,易知AE= c,这时我们把关于x的形如ax²+ cx+b=0的一元二次方程称为“勾系一元二次方程”。请解决下列问题: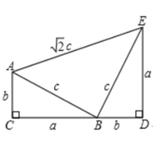 (1)、求证:关于x的“勾系一元二次方程”ax²+ cx+b=0必有实数根;(2)、若x=-1是“勾系一元二次方程”ax²+ cx+b=0的一个根,且四边形ACDE的周长是12,求△ABC的面积。24. 如图,在Rt△ABC中,∠ABC=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动。设点D、E运动的时间是t/s(0<t≤15)。过点D作DF⊥BC于点F,连结DE,EF。
(1)、求证:关于x的“勾系一元二次方程”ax²+ cx+b=0必有实数根;(2)、若x=-1是“勾系一元二次方程”ax²+ cx+b=0的一个根,且四边形ACDE的周长是12,求△ABC的面积。24. 如图,在Rt△ABC中,∠ABC=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动。设点D、E运动的时间是t/s(0<t≤15)。过点D作DF⊥BC于点F,连结DE,EF。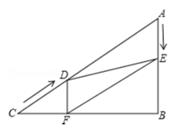 (1)、求证:AE=DF;(2)、四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;(3)、当t为何值时,△DEF为直角三角形?请说明理由。
(1)、求证:AE=DF;(2)、四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;(3)、当t为何值时,△DEF为直角三角形?请说明理由。