浙江省金华市2020年数学中考复习卷（一）

试卷更新日期：2020-04-28 类型：中考模拟

进入出卷网下载

一、选择题(本题有10小题，每小题3分，共30分)

1. $- \frac{1}{2}$ 的倒数等于（）

A、 $\frac{1}{2}$ B、-2 C、2 D、 $- \frac{1}{2}$

查看试题解析
2. 下列计算正确的是（）

A、2³×2²=2⁶ B、 ${(- \frac{1}{2})}^{3} = - \frac{1}{6}$ C、 $- \frac{1}{2} + \frac{1}{3} = - \frac{5}{6}$ D、-3²=-9

查看试题解析
3. 据测算，我国每天因土地沙漠化造成的损失约为150 000 000元，将150 000 000用科学记数法表示为（）

A、1.5×10⁷ B、15×10⁷ C、1.5×10⁸ D、0.15×10⁹

查看试题解析
4. 如图所示的几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
5. 不等式组 ${\begin{cases} 2 x + 1 \geq - 3 \\ x < 1 \end{cases}$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
6. 新能源汽车环保节能，越来越受到消费者的喜爱，各种品牌相继投放市场，一汽贸公司经销某品牌新能源汽车，去年销售总额为5000万元，今年1~3月份，每辆车的销售价格比去年降低1万元，销售数量与去年一整年的相同，销售总额比去年一整年的少20%，今年1~3月份每辆车的销售价格是多少万元？设今年1~3月份每辆车的销售价格为x万元，则可列方程为（）

A、 $\frac{5000}{x + 1} = \frac{5000 (1 - 20 %)}{x}$ B、 $\frac{5000}{x + 1} = \frac{5000 (1 + 20 %)}{x}$ C、 $\frac{5000}{x - 1} = \frac{5000 (1 - 20 %)}{x}$ D、 $\frac{5000}{x - 1} = \frac{5000 (1 + 20 %)}{x}$

查看试题解析
7. 下列三幅图都是“作已知三角形的高”的尺规作图过程，其中作图依据相同的是（）

A、(1)(2) B、(1)(3) C、(2)(3) D、(1)(2)(3)

查看试题解析
8. 如图，点E从点A出发沿AB方向运动，点G从点B出发沿BC方向运动，同时出发且速度相同，DE=GF<AB(DE长度不变，F在G上方，D在E左边)，当点D到达点B时，点E停止运动．在整个运动过程中，图中阴影部分面积的大小变化情况是（）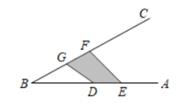

A、一直减小 B、一直不变 C、先减小后增大 D、先增大后减小

查看试题解析
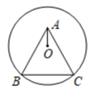
9. 甲、乙两车从A地出发，匀速驶向B地，甲车以80km/h的速度行驶1h后，乙车才沿相同路线行驶，乙车先到达B地并停留1h后，再以原速沿原路返回，直至与甲车相遇。在此过程中，两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示。下列说法错误的是（）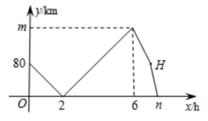

A、乙车的速度是120km/h B、m=160 C、点H的坐标是(7，80) D、n=7.5

查看试题解析
10. 如图，在等边三角形ABC的AC，BC边上分别任取一点P，Q，且AP=CQ，AQ、BP相交于点O。下列四个结论：①若PC=2AP，则BO=6OP；②若BC=8，BP=7，则PC=5；③AP²=OP·AQ；④若AB=3，则OC的最小值为 $\sqrt{3}$ ，其中正确的是（）

A、①②④ B、①③④ C、②③④ D、①②③

查看试题解析

二、填空题(本题有6小题，每小题4分，共24分)

11. 如果反比例函数y= $\frac{k}{x}$ 的图象经过点A(1，2)，那么k的值是。

查看试题解析
12. 若将抛物线y=x²+x先向右平移1个单位长度，再向下平移2个单位长度，则平移后的抛物线所对应的函数解析式为。

查看试题解析
13. 从2，3，4，5，6，7，8，9中随机选出一个数，所选的数是2的倍数或3的倍数的概率为。

查看试题解析
14. 如图，BC是⊙O的弦，以BC为边作等边三角形ABC，圆心O在△ABC的内部，若BC=6，OA= $\sqrt{3}$ ，则⊙O的半径为。

查看试题解析
15. 如图，△ABC是等腰直角三角形，∠A=90°，AB=1，∠CDA=∠EDB，CE=DE，那么CE=。

查看试题解析
16. 如图，点A(-1，0)，点P是射线AO上一动点(不与O点重合)，过点P作直线y=x的平行线交y轴于C，过点P作x轴的垂线交直线y=x于B，连结AB，AC，BC。

(1)、当点P在线段OA上且AP=PC时，AB：BC=；

(2)、当△ABC与△OPC相似时，P点的横坐标为。

查看试题解析

三、解答题(本题有8小题，共66分)

17. 计算：3^-1-4cos45°+ $\sqrt{8}$ -|-2|

查看试题解析
18. 有三张正面分别写有数字1，3，4的卡片，它们的背面完全相同，将这三张卡片背面朝上洗匀后随机抽取一张，以其正面的数字作为a的值，把方程组 ${\begin{cases} x + a y = 3 \\ x + 2 y = 2 \end{cases}$ 的解记为平面直角坐标系中点A的坐标(x，y)，求点A在第四象限的概率。

查看试题解析
19. 如图，△ABC与△CDE都是等腰直角三角形，∠ACB=∠DCE=90°，AC=6，点E在点A右侧，AE=3，∠CAE=45°。

(1)、求证：△BCE≌△ACD；

(2)、求AD的长。

查看试题解析
20. 为了发展乡村旅游，建设美丽乡村，某中学七年级(1)班同学都积极参加了植树活动，将今年三月份该班同学的植树情况绘制成如图所示的不完整的统计图。已知植树量为2株的人数占总人数的32%。

(1)、该班的总人数为，植树株数的众数是，植树株数的中位数是；

(2)、请将条形统计图补充完整；

(3)、若将该班同学的植树情况绘制成扇形统计图，求“植树量为3株”所对应的扇形的圆心角度数。

查看试题解析
21. 如图，在Rt△ABC中，∠C=90°，AC=BC，点O在AB上，以O为圆心，OA为半径作⊙O，与BC相切于点D，且交AB于点E。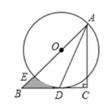

(1)、连结AD，求证：AD平分∠CAB；

(2)、若BE= $\sqrt{2}$ -1，求阴影部分的面积。

查看试题解析
22. 随着某市养老机构(养老机构指社会福利院、养老院、社区养老中心等)建设稳步推进，拥有的养老床位及养老建筑不断增加。

(1)、该市的养老床位数从2017年底的2万个增长到2019年底的2.88万个，求该市这两年(从2017年底到2019年底)拥有的养老床位数的平均年增长率；

(2)、该市某社区今年准备新建一养老中心，如果计划赡养200名老人，建筑投入平均5万元/人，且计划赡养的老人每增加5人，建筑投入平均减少1000元/人，那么新建该养老中心需申报的最高建筑投入是多少？

查看试题解析
23. 定义：在方格纸中，每个小格的顶点叫做格点，以格点为顶点的三角形叫做格点三角形．已知图1，图2中的每一个小方格的边长都为1。

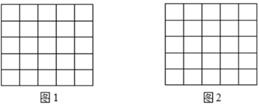(1)、△ABC的三边长为AB= $\sqrt{5}$ ，BC= $\sqrt{10}$ ，CA=5。
①在图1中画一个符合题意的△ABC；

②求△ABC的边BC上的高线长；

(2)、在5×5的方格纸纸板中最多能剪下(要完整不拼凑)多少个与(1) 中△ABC全等的三角形？并在图2中设计出来。

查看试题解析
24. 如图，在平面直角坐标系中，O为坐标原点，点A(-2，0)，点B(0，2)，点C为OA中点，点C与点D关于y轴对称。

(1)、点D的坐标为；

(2)、连结BC，求∠CBD的正切值；

(3)、抛物线y= $- \frac{25}{46} x^{2} + b x + \frac{79}{23}$ 的对称轴为直线x= $\frac{53}{50}$ ，在抛物线上是否存在点E(E、A不重合)，使△EBD与△ABD全等？若存在，求出点E的坐标；若不存在，请说明理由。

查看试题解析