浙江省杭州市2019-2020学年七年级下学期数学期中考试试卷

试卷更新日期：2020-04-28 类型：期中考试

进入出卷网下载

一、选择题：本大题有10个小题，每小题3分，共30分．

1. 把多项式a²-a分解因式，结果正确的是（）

A、a(a-1) B、(a+1)(a-1) C、a(a+1)(a-1) D、-a(a-1)

查看试题解析
2. 下列图形中，能由∠1=∠2得到AB∥CD的是（）

A、 B、 C、 D、

查看试题解析
3. 已知方程 $\frac{x}{2} - \frac{y}{3} = 5$ ，用含x的代数式表示y，正确的是（）

A、 $y = \frac{3}{2} x - \frac{5}{2}$ B、 $y = \frac{3}{2} x - 15$ C、 $y = - \frac{3}{2} x - \frac{5}{2}$ D、 $y = - \frac{3}{2} x - 15$

查看试题解析
4. 下列运算正确的是（）

A、(a+b)²=a²+b² B、2a³·3a²=6a⁶ C、(m-n)⁶÷(n-m)³=(n-m)³ D、(-2x³)⁴=8x¹²

查看试题解析
5. 二元一次方程3x+4y=20的正整数解有（）

A、1组 B、2组 C、3组 D、4组

查看试题解析
6. 下列从左到右的变形中是因式分解的有（）
①(p-2)(p+2)=p²-4，②4x²-4x+1=(2x-1)²，③a²+2ab+b²-1=a(a+2b)+(b+1)(b-1)，④(a+b)(a-b)+(b-a)=(a-b)(a+b-1)

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 某出租车起步价所包含的路程为0~2km，超过2km的部分按每千米另收费。津津乘坐这种出租车走了7km，付了16元；盼盼乘坐这种出租车走了13km，付了28元。设这种出租车的起步价为x元，超过2km后每千米收费y元，则所列方程组正确的是（）

A、 ${\begin{cases} x + 7 y = 16 \\ x + 13 y = 28 \end{cases}$ B、 ${\begin{cases} x + (7 - 2) y = 16 \\ x + 13 y = 28 \end{cases}$ C、 ${\begin{cases} x + 7 y = 16 \\ x + (13 - 2) y = 28 \end{cases}$ D、 ${\begin{cases} x + (7 - 2) y = 16 \\ x + (13 - 2) y = 28 \end{cases}$

查看试题解析
8. 如果9x²-kx+25是一个完全平方式，那么k的值是（）

A、15 B、30 C、±30 D、±60

查看试题解析
9. 如图，AB∥EF，用含∠1，∠2，∠3的式子表示∠4，则∠4等于（）

A、∠1+∠2-∠3 B、∠1+∠3-∠2 C、180°+∠3-∠1-∠2 D、∠2+∠3-∠1-180°

查看试题解析
10. 有两个正方形A，B，现将B放在A的内部如图甲，将A，B并排放置后构造新的正方形如图乙。若图甲和图乙中阴影部分的面积分别为 $\frac{1}{4}$ 和 $\frac{13}{4}$ ，则正方形A，B的面积之和为（）

A、3 B、3.5 C、4 D、4.5

查看试题解析

二、填空题：本大题有6个小题，每小题4分，共24分。

11. 某种病毒的直径是0.00000008米，这个数据用科学记数法表示为米。

查看试题解析
12. 因式分解4(a-b)²-8a+8b的结果是。

查看试题解析
13. 如图，把一张长方形纸条ABCD沿EF折叠，若∠BGD'为x度，则∠1的度数应为度(用含x的代数式表示)。

查看试题解析
14. 已知关于x，y的二元一次方程2x-3y=t，其部分值如下表所示，则p的值是。

x

m

m+2

y

n

n-2

t

5

p

查看试题解析
15. 有一列数，按一定规律排列成1，-2，4，-8，16，-32，…，其中某三个相邻数的积是 $4^{12}$ ，则这三个数的和是.

查看试题解析
16. 关于x，y的方程组 ${\begin{cases} 3 x - 5 y = 2 a \\ 2 x + 7 y = a - 18 \end{cases}$ ，有下列三种说法：①当a=8时，x，y互为相反数；②x，y都是负整数的解只有1组；③ ${\begin{cases} x = 21 \\ y = - 3 \end{cases}$ 是该方程组的解。其中说法正确的有 (填序号)。

查看试题解析

三、解答题：本大题有7个小题，共66分．解答应写出文字说明、证明过程或演算步骤。

17. 计算：

(1)、 $3 \times {(- \frac{1}{42})}^{0} - \sqrt{16} + {(\frac{1}{2})}^{- 1}$

(2)、(4ab³-8a²b²)÷4ab+2a(2a-b)

查看试题解析
18. 因式分解：

(1)、2x³-8xy²

(2)、(m²-4m)²+8(m²-4m)+16

查看试题解析
19. 解方程组：

(1)、 ${\begin{cases} 2 x - 5 y + 13 = 0 \\ 9 x + 6 y - 8 = 0 \end{cases}$

(2)、 ${\begin{cases} 3 (x + y) - 4 (x - y) = 4 \\ \frac{x + y}{2} + \frac{x - y}{6} = 1 \end{cases}$

查看试题解析
20. 先化简，再求值：

(1)、(a+1)²-(a+2)(a一3)，其中 $\sqrt{5}$ <a< $\sqrt{10}$ ，且a是整数。

(2)、已知2x²+3x-6=0，求代数式3x(2x+1)-(2x+1)(2x-1)的值。

查看试题解析

21. 杭州市实行“五水共治”，为鼓励市民节约用水，居民生活用水按阶梯式水价计费．下表是居民“一户一表”生活用水阶梯式计费价格表部分信息：

每户每月用水量	自来水销售价格 (单位：元/吨)	污水处理价格 (单位：元/吨)
17吨及以下	a	0.80
超过17吨但不超过30吨的部分	b	0.80
超过30吨的部分	6.00	0.80

(说明：①每户产生的污水量等于该户自来水用水量；②水费=自来水费用+污水处理费)

已知小王家2019年四月份用水20吨，交水费66元；五月份用水25吨，交水费91元。

(1)、求a，b的值。

(2)、随着夏天的到来，用水量将增加，小王家六月份的水费是家庭月收入的2%，若小王家的月收入为9200元，求小王家六月份的用水量是多少吨？

查看试题解析

22. 如图，∠ABC和∠BCD的平分线交于点P，延长CP交AB于点Q，且∠PBC+∠PCB=90°。

(1)、求证：AB∥CD。

(2)、探究∠PBC与∠PQB的数量关系。

查看试题解析
23. 已知D是△ABC的BC边上一点，连结AD，此时有结论 $\frac{S_{△ A B D}}{S_{△ A C D}} = \frac{B D}{C D}$ ，请解答下列问题：

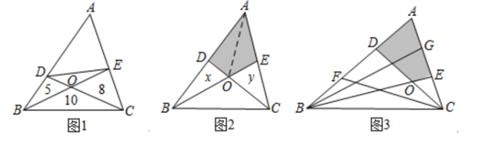(1)、当D是BC边上的中点时，△ABD的面积 △ACD的面积(填“>”“<”或“=”)。

(2)、如图1，点D、E分别为AB，AC边上的点，连结CD，BE交于点O，若△BOD、△COE、△BOC的面积分别为5，8，10，则△ADE的面积是(直接写出结论)。

(3)、如图2，若点D，E分别是△ABC的AB，AC边上的中点，且S_△_ABC=60，求四边形ADOE的面积。可以用如下方法：连结AO，由AD=DB得S_△_ADO=S_△_BDO ，同理：S_△CEO=S_△AEO ，设S_△BDO=x，S_△CEO=y，则S_△ADO=x，S_△AEO=y，由题意得S_△ABE= $\frac{1}{2}$ S_△ABC=30，S_△ADC= $\frac{1}{2}$ S_△ABC=30，可列方程组为 ${\begin{cases} 2 x + y = 30 \\ x + 2 y = 30 \end{cases}$ ，解得x+y=20，可得四边形ADOE的面积为20。解答下面问题：
如图3，D，F是AB的三等分点，E，G是CA的三等分点，CD与BE交于O，且S_△_ABC=60，请计算四边形ADOE的面积，并说明理由。

查看试题解析

x	m	m+2
y	n	n-2
t	5	p