浙江省杭州市2019-2020学年八年级下学期数学期中考试试卷
试卷更新日期：2020-04-28 类型：期中考试
一、选择题：本大题有10个小题，每小题3分，共30分．
-
1. 下列图形既是轴对称图形，又是中心对称图形的是（ ）A、线段 B、等腰三角形 C、平行四边形 D、等边三角形2. 计算 的结果是（ ）A、±3 B、-3 C、3 D、93. 下面是甲、乙两人10次射击成绩（环数）的条形统计图，则下列说法正确的是（ ）
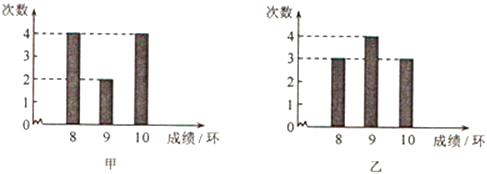A、甲比乙的成绩稳定 B、乙比甲的成绩稳定 C、甲、乙两人的成绩一样稳定 D、无法确定谁的成绩更稳定4. 如图，在 ABCD中，AC与BD交于点O，下列说法一定正确的是（ ）
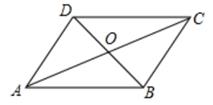A、AC=BD B、AC⊥BD C、AO=CO D、AB=BC5. 已知关于x的方程(m+1)x²-3=0是一元二次方程，则m的取值范围是（ ）A、m>-1 B、m≠0 C、m≤-1 D、m≠-16. 点点同学对数据26，36，46，
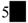，52进行统计分析，发现其中一个两位数的个位数字被墨水涂污看不到了，则计算结果与被涂污数字无关的是（ ） A、平均数 B、中位数 C、方差 D、标准差7. 某超市一月份的营业额为200万元，三月份的营业额为288万元，若每月比上月营业额增长的百分率相同，则每月营业额增长的百分率为（ ）A、10% B、15% C、20% D、25%8. 设 =m， =n，则 可以表示为（ ）A、 B、 C、 D、9. 如图，在平行四边形ABCD中，点O是对角线AC上一点，连结BO，DO，△COD，△AOD，△AOB，△BOC的面积分别是S1 ， S2 ， S3 ， S4。下列关于S1 ， S2 ， S3 ， S4的等量关系式中错误的是（ ）
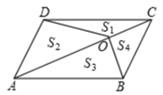A、S1+S3=S2+S4 B、 C、S3-S1=S2-S4 D、S2=2S110. 已知一元二次方程a(x-x1)(x-x2)=0(a≠0，x1≠x2)与一元一次方程dx+e=0有一个公共解x=x1 ， 若一元二次方程a(x-x1)(x-x2)+(dx+e)=0有两个相等的实数根，则（ ）A、a(x1-x2)=d B、a(x2-x1)=d C、a(x1-x2)²=d D、a(x2-x1)2=d二、填空题：本大题有6个小题，每小题4分，共24分。
-
11. 要使二次根式 有意义，则a的取值范围是。12. 已知多边形的内角和等于外角和的两倍，则这个多边形的边数为。13. 在 ABCD中，∠D=65°，过点C作CE⊥AB于E，则∠BCE的度数为。14. 据统计，某车间10名员工的日平均生产零件个数为8个，方差为2.5个²。引入新技术后，每名员工每天都比原先多生产1个零件，则现在日平均生产零件个数为个，方差为个2。15. 已知一元二次方程2x²+bx+c=0的两个根为x1=1和x2=2，则b= ， c=。16. 若a= ，则a3-a+1=。
三、解答题：本大题有7个小题，共66分．解答应写出文字说明、证明过程或演算步骤。
-
17. 计算：(1)、(2)、18. 用适当方法解下列方程：(1)、(3x-1)²=9(2)、x(2x-4)=(2-x)²(3)、 x2-2x- =019. 某学校抽查了某班级某月5天的用电量，数据如下表：
用电量(单位：度)
9
10
11
天数
3
1
1
(1)、求这5天的平均用电量。(2)、求这5天用电量的众数、中位数。(3)、该学校共有36个班级，若一个月按22天计算，试估计该校该月的总用电量。20. 设实数 的整数部分为a，小数部分为b。(1)、计算：|b- |(2)、求(2a+b)(2a-b)的值。21. 为了宣传垃圾分类，小王写了一封倡议书，用微博转发的方式传播，他设计了如下的转发规则：将倡议书发表在自己的微博上，然后邀请x个好友转发，每个好友转发之后，又邀请x个互不相同的好友转发，已知经过两轮转发后，共有111个人参与了本次活动。(1)、x的值是多少？(2)、再经过几轮转发后，参与人数会超过10000人？22. 如图，在△ABC中，∠ACB=90°，以点B为圆心，BC长为半径画弧，交线段AB于点D，连结CD，以点A为圆心，AC长为半径画弧，交线段AB于点E，连结CE。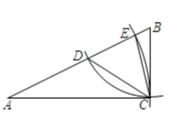
(1)、求∠DCE的度数。(2)、设BC=a，AC=b。①线段BE的长是关于x的方程x²+2bx-a²=0的一个根吗？说明理由。
②若D为AE的中点，求 的值。
23. 在▱ABCD中，对角线AC，BD交于点O，且分别平分∠DAB，∠ABC。(1)、请求出∠AOB的度数，写出AD，AB，BC之间的等量关系，并给予证明。(2)、设点P为对角线AC上一点，PB=5，若AD+BC=16，四边形ABCD的面积为 ，求AP的长。