山东省淄博市淄川区2019年中考数学二模考试试卷

试卷更新日期：2020-04-28 类型：中考模拟

进入出卷网下载

一、选择题

1. 下列实数中，与4最接近的是（）

A、3.5 B、 $\sqrt{13}$ C、 $\sqrt{17}$ D、 $\sqrt{19} - 13$

查看试题解析
2. 分式方程 $\frac{3}{x} = \frac{2}{x - 1}$ 的解是（）

A、 $x = - 3$ B、 $x = - \frac{3}{5}$ C、 $x = 3$ D、无解

查看试题解析
3. 下列事件：
①在足球赛中，弱队战胜强队．②抛掷1枚硬币，硬币落地时正面朝上．③任取两个正整数，其和大于1④长为3cm，5cm，9cm的三条线段能围成一个三角形．其中确定事件有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 下列运算中，不正确的是（）

A、 $\frac{a - b}{a + b} = \frac{b - a}{b + a}$ B、 $\frac{- a - b}{a + b} = - 1$ C、 $\frac{0.5 a + b}{0.2 a - 0.3 b} = \frac{5 a + 10 b}{2 a - 3 b}$ D、 $\frac{{(a - b)}^{2}}{{(b - a)}^{2}} = 1$

查看试题解析
5. 观察如图所示的三种视图，与之对应的物体是（）

A、 B、 C、 D、

查看试题解析
6. 若反比例函数的图象经过点 $A (- 3, 6)$ ，在这个函数的图象上任取点 $B (a, m)$ 和点 $C (b, n)$ ．若 $a > b > 0$ ，则下列式子中正确的是（）

A、 $m < n$ B、 $m > n$ C、 $m n < 0$ D、 $a m > b n$

查看试题解析
7. 若数 $a$ 使关于 $x$ 的不等式 $5 x - 2 \geq x + a$ 的最小正整数解是 $x = 1$ ，则 $a$ 的取值范围是（）

A、 $a > - 2$ B、 $a < 2$ C、 $- 2 < a < 2$ D、 $a \leq 2$

查看试题解析
8. 把一副三角板放在同一水平桌面上，摆放成如图所示的形状，使两个直角顶点重合，两条斜边平行，则∠1的度数是（）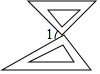

A、45° B、60° C、75° D、82.5°

查看试题解析
9. 为了解中学生获取信息的主要渠道，设置“A：报纸，B：电视，C：网络，D：身边的人，E：其他”五个选项（五项中必选且只能选一项）的调查问卷，先随机抽取50名中学生进行该问卷调查，根据调查的结果绘制条形图如图，该调查的方式和图中a的值分别是（）

A、抽样调查，24 B、普查，24 C、抽样调查，26 D、普查，26

查看试题解析
10. 已知直线y₁=kx+1（k＜0）与直线y₂=mx（m＞0）的交点坐标为（ $\frac{1}{2}$ ， $\frac{1}{2}$ m），则不等式组mx﹣2＜kx+1＜mx的解集为（）

A、x> $\frac{1}{2}$ B、 $\frac{1}{2}$ <x< $\frac{3}{2}$ C、x< $\frac{3}{2}$ D、0<x< $\frac{3}{2}$

查看试题解析
11. 如图，在矩形ABCD中，AD=2AB，点M、N分别在边AD、BC上，连接BM、DN．若四边形MBND是菱形，则 $\frac{A M}{M D}$ 等于（）

A、 $\frac{3}{5}$ B、 $\frac{2}{3}$ C、 $\frac{3}{8}$ D、 $\frac{4}{5}$

查看试题解析
12. 若抛物线 $y = x^{2} + a x + b$ 与 $x$ 轴两个交点间的距离为2，称此抛物线为定弦抛物线，已知某定弦抛物线的对称轴为直线 $x = 1$ ，将此抛物线向左平移2个单位，再向下平移3个单位，得到的抛物线过点（）

A、 $(- 3 ， - 6)$ B、 $(- 3 ， 0)$ C、 $(- 3 ， - 5)$ D、 $(- 3 ， - 1)$

查看试题解析

二、填空题

13. 顺次连接正方形各边中点，得到一个新正方形，则新正方形与原正方形的相似比是．

查看试题解析
14. 请你写出一个既能提取公因式，用后又能用十字相乘法分解因式的多项式：．

查看试题解析
15. 如图，已知点 $C$ 是 $⊙ O$ 的直径 $A B$ 上的一点，过点 $C$ 作弦 $D E$ ，使 $C D = C O$ ．若 $\overset{⌢}{A D}$ 的度数为40°，则 $\overset{⌢}{B E}$ 的度数是．

查看试题解析
16. 如图，直线 $y = - \frac{\sqrt{3}}{3} x + 4$ 与 $x$ 轴、 $y$ 轴分别交于A，B两点，C是OB的中点，D是AB上一点，四边形OEDC是菱形，则△OAE的面积为．

查看试题解析
17. 如图，在直角△ABC中，∠C=90°，AC=6，BC=8，P、Q分别为边BC、AB上的两个动点，若要使△APQ是等腰三角形且△BPQ是直角三角形，则AQ=.

查看试题解析

三、综合题

18. 已知，如图，∠1+∠2=180° ，求证：∠3=∠4.

查看试题解析
19. 一艘船由 $A$ 港沿北偏东60°方向航线10 $k m$ 至 $B$ 港，然后再沿北偏西30°方向航行10 $k m$ 至 $C$ 港．

(1)、求 $A$ ， $C$ 两港之间的距离；

(2)、确定 $C$ 港在 $A$ 港的什么方向？（画出示意图，并解答）

查看试题解析
20. 某校260名学生参加植树活动，要求每人植树4~7棵，活动结束后随机抽查了20名学生每人的植树量，并分为四种类型，A：4棵；B：5棵；C：6棵；D：7棵．将各类的人数绘制成扇形图（如图1）和条形图（如图2），经确认扇形图是正确的，而条形图尚有一处不符合题意．

回答下列问题：

(1)、写出条形图中存在的不符合题意，并说明理由；

(2)、写出这20名学生每人植树量的众数和中位数；

(3)、求这20名学生每人植树量的平均数，并估计这260名学生共植树多少棵？

查看试题解析
21. 如图，在足够大的空地上有一段长为a米的旧墙MN，某人利用旧墙和木栏围成一个矩形菜园ABCD，其中AD≤MN，已知矩形菜园的一边靠墙，另三边一共用了100米木栏．

(1)、若a=20，所围成的矩形菜园的面积为450平方米，求所利用旧墙AD的长；

(2)、求矩形菜园ABCD面积的最大值．

查看试题解析
22. 已知关于 $x$ 的一元二次方程 $m^{2} x^{2} + (1 - 2 m) x + 1 = 0$ 有两个不相等的实数根．

(1)、求实数 $m$ 的取值范围；

(2)、若原方程的两个实数根分别为 $x_{1}$ ， $x_{2}$ ，且满足 $| x_{1} | + | x_{2} | = 2 x_{1} x_{2} - 15$ ，求 $m$ 的值．

查看试题解析
23. 如图

(1)、问题：如图1，在四边形ABCD中，点P为AB上一点，∠DPC=∠A=∠B=90°．求证：AD·BC=AP·BP．

(2)、探究：如图2，在四边形ABCD中，点P为AB上一点，当∠DPC=∠A=∠B=θ时，上述结论是否依然成立．说明理由．

(3)、应用：请利用（1）（2）获得的经验解决问题：
如图3，在△ABD中，AB=6，AD=BD=5．点P以每秒1个单位长度的速度，由点A 出发，沿边AB向点B运动，且满足∠DPC=∠A．设点P的运动时间为t（秒），当DC的长与△ABD底边上的高相等时，求t的值．

查看试题解析
24. 如图，抛物线y=ax²+bx+2经过点A(−1，0)，B(4，0)，交y轴于点C；

(1)、求抛物线的解析式(用一般式表示)；

(2)、点D为y轴右侧抛物线上一点，是否存在点D使S_△ABC= $\frac{2}{3}$ S_△ABD?若存在，请求出点D坐标；若不存在，请说明理由；

(3)、将直线BC绕点B顺时针旋转45°，与抛物线交于另一点E，求BE的长.

查看试题解析