山东省泰安市肥城市2019年中考数学二模考试试卷
试卷更新日期:2020-04-28 类型:中考模拟
一、选择题
-
1. 2019的相反数的倒数是( )A、 B、 C、-2019 D、20192. “厉行勤俭节约,反对铺张浪费”势在必行,最新统计数据显示,中国每年浪费食物总量折合粮食大约是210000000人一年的口粮.将210000000用科学记数法表示为( )A、2.1×109 B、0.21×109 C、2.1×108 D、21×1073. 下列图形中,可以由其中一个图形通过平移得到的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 某校四个环保小组一天收集废纸的数量分别为:10,x,9,8,(单位千克)已知这组数据的众数与平均数相等,则这组数据的中位数是( )A、8.5 B、9 C、9.5 D、86. 下图是一张直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则DE的长为( )
4. 下列运算正确的是( )A、 B、 C、 D、5. 某校四个环保小组一天收集废纸的数量分别为:10,x,9,8,(单位千克)已知这组数据的众数与平均数相等,则这组数据的中位数是( )A、8.5 B、9 C、9.5 D、86. 下图是一张直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则DE的长为( )
 A、4cm B、5cm C、 D、7.
A、4cm B、5cm C、 D、7.数学课上,老师让学生尺规作图画Rt△ABC,使其斜边AB=c,一条直角边BC=a.小明的作法如图所示,你认为这种作法中判断∠ACB是直角的依据是( )
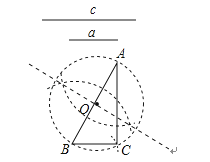 A、勾股定理 B、直径所对的圆周角是直角 C、勾股定理的逆定理 D、90°的圆周角所对的弦是直径8. 关于x的不等式组 有四个整数解,则a的取值范围是( )A、﹣ <a≤﹣ B、﹣ ≤a<﹣ C、﹣ ≤a≤﹣ D、﹣ <a<﹣9. 一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后分别按原速同时驶往甲地,两车之间的距离S(km)与慢车行驶时间t(h)之间的函数图象如图所示,下列说法:
A、勾股定理 B、直径所对的圆周角是直角 C、勾股定理的逆定理 D、90°的圆周角所对的弦是直径8. 关于x的不等式组 有四个整数解,则a的取值范围是( )A、﹣ <a≤﹣ B、﹣ ≤a<﹣ C、﹣ ≤a≤﹣ D、﹣ <a<﹣9. 一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后分别按原速同时驶往甲地,两车之间的距离S(km)与慢车行驶时间t(h)之间的函数图象如图所示,下列说法:①甲、乙两地之间的距离为560km;②快车速度是慢车速度的1.5倍;③快车到达甲地时,慢车距离甲地60km;④相遇时,快车距甲地320km;其中正确的个数是( )
 A、1个 B、2个 C、3个 D、4个10. 如图,一次函数y=k1x+b的图象与反比例函数y= 的图象相交于A(2,3),B(6,1)两点,当k1x+b< 时,x的取值范围为( )
A、1个 B、2个 C、3个 D、4个10. 如图,一次函数y=k1x+b的图象与反比例函数y= 的图象相交于A(2,3),B(6,1)两点,当k1x+b< 时,x的取值范围为( )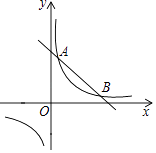 A、x<2 B、2<x<6 C、x>6 D、0<x<2或x>611. 如图, ,射线 和 互相垂直,点 是 上的一个动点,点 在射线 上, ,作 并截取 ,连结 并延长交射线 于点 .设 ,则 关于 的函数解析式是( )
A、x<2 B、2<x<6 C、x>6 D、0<x<2或x>611. 如图, ,射线 和 互相垂直,点 是 上的一个动点,点 在射线 上, ,作 并截取 ,连结 并延长交射线 于点 .设 ,则 关于 的函数解析式是( ) A、 B、 C、 D、12. 如图所示为二次函数 的图象,在下列结论
A、 B、 C、 D、12. 如图所示为二次函数 的图象,在下列结论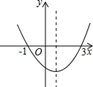
① ;② 时, 随 的增大而增大;③ ;④方程 的根是 ;中正确的个数有( )个.
A、1 B、2 C、3 D、4二、填空题
-
13. .14. 已知如图, 平分 ,当 ,且 时, 的度数为 .
 15. 如图,在正方形 中,对角线 与 相交于点 , 为 上一点, , 为 的中点.若 的周长为18,则 的长为 .
15. 如图,在正方形 中,对角线 与 相交于点 , 为 上一点, , 为 的中点.若 的周长为18,则 的长为 . 16. 如图,某高速公路建设中需要测量某条江的宽度AB,飞机上的测量人员在C处测得A,B两点的俯角分别为 和 若飞机离地面的高度CH为1200米,且点H,A,B在同一水平直线上,则这条江的宽度AB为米 结果保留根号 .
16. 如图,某高速公路建设中需要测量某条江的宽度AB,飞机上的测量人员在C处测得A,B两点的俯角分别为 和 若飞机离地面的高度CH为1200米,且点H,A,B在同一水平直线上,则这条江的宽度AB为米 结果保留根号 .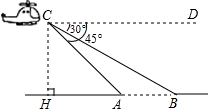 17. 如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点 处,当△ 为直角三角形时,BE的长为.
17. 如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点 处,当△ 为直角三角形时,BE的长为. 18. 如图,动点 在平面直角坐标系中按图中箭头所示的方向运动,第1次从原点运动到(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),...按这样的运动规律,经过2019次运动后,动点 的坐标为 .
18. 如图,动点 在平面直角坐标系中按图中箭头所示的方向运动,第1次从原点运动到(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),...按这样的运动规律,经过2019次运动后,动点 的坐标为 .
三、计算题
-
19. 先化简,再求值: ,其中 .
四、综合题
-
20. 如图,在平面直角坐标中,点 是坐标原点,一次函数 与反比例函数 的图象交于 两点.
 (1)、求 的值.(2)、根据图象写出当 时, 的取值范围.(3)、若一次函数图象与 轴、 轴分别交于点 ,则求出 的面积.21. 随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)、求 的值.(2)、根据图象写出当 时, 的取值范围.(3)、若一次函数图象与 轴、 轴分别交于点 ,则求出 的面积.21. 随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题: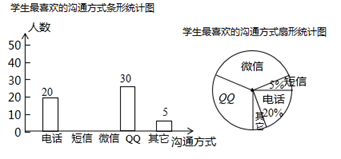 (1)、这次统计共抽查了多少名学生?在扇形统计图中,表示" "的扇形圆心角的度数是多少;(2)、将条形统计图补充完整;(3)、该校共有1500名学生,请估计该校最喜欢用 “微信”进行沟通的学生大约有多少名?(4)、某天甲、乙两名同学都想从“微信"、" "、“电话"三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.22. 如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)、这次统计共抽查了多少名学生?在扇形统计图中,表示" "的扇形圆心角的度数是多少;(2)、将条形统计图补充完整;(3)、该校共有1500名学生,请估计该校最喜欢用 “微信”进行沟通的学生大约有多少名?(4)、某天甲、乙两名同学都想从“微信"、" "、“电话"三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.22. 如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F. (1)、求证:△AEC≌△ADB;(2)、若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.23. 某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求.商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.(1)、该商家购进的第一批衬衫是多少件?(2)、若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润率不低于25%(不考虑其它因素),那么每件衬衫的标价至少是多少元?24. 如图,二次函数 的图象交x轴于A、B两点,交y轴于点D , 点B的坐标为 ,顶点C的坐标为 .
(1)、求证:△AEC≌△ADB;(2)、若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.23. 某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求.商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.(1)、该商家购进的第一批衬衫是多少件?(2)、若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润率不低于25%(不考虑其它因素),那么每件衬衫的标价至少是多少元?24. 如图,二次函数 的图象交x轴于A、B两点,交y轴于点D , 点B的坐标为 ,顶点C的坐标为 . (1)、求二次函数的解析式和直线BD的解析式;(2)、点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M , 当点P在第一象限时,求线段PM长度的最大值;(3)、在抛物线上是否存在异于B、D的点Q , 使 中BD边上的高为 ?若存在求出点Q的坐标;若不存在请说明理由.25. 等腰直角 和等腰直角 分别在直线 上.(1)、如图所示, 分别在线段 上,若 ,求证: .
(1)、求二次函数的解析式和直线BD的解析式;(2)、点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M , 当点P在第一象限时,求线段PM长度的最大值;(3)、在抛物线上是否存在异于B、D的点Q , 使 中BD边上的高为 ?若存在求出点Q的坐标;若不存在请说明理由.25. 等腰直角 和等腰直角 分别在直线 上.(1)、如图所示, 分别在线段 上,若 ,求证: . (2)、若 分别在线段 外(还在直线 上),根据题意,画出图形,那么(1)的结论是否依然成立,若成立,写出证明过程;若不成立,说明原因;(3)、如图,若 ,求证: .
(2)、若 分别在线段 外(还在直线 上),根据题意,画出图形,那么(1)的结论是否依然成立,若成立,写出证明过程;若不成立,说明原因;(3)、如图,若 ,求证: .
-