山东省济宁市金乡县2019年中考数学5月模拟考试试卷
试卷更新日期:2020-04-28 类型:中考模拟
一、选择题
-
1. 的相反数是( )A、 B、5 C、 D、2. 把0.0813写成a×10n(1≤a<10,n为整数)的形式,则a为( )A、1 B、﹣2 C、0.813 D、8.133. 下列立体图形中,主视图是三角形的是( )A、
 B、
B、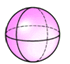 C、
C、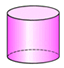 D、
D、 4. 如图,直线 被 所截,且 ,则下列结论中正确的是( )
4. 如图,直线 被 所截,且 ,则下列结论中正确的是( )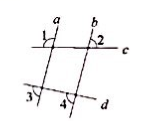 A、 B、 C、 D、5. 已知x1、x2是关于x的方程x2﹣ax﹣2=0的两根,下列结论一定正确的是( )A、x1≠x2 B、x1+x2>0 C、x1•x2>0 D、x1<0,x2<06. 在只有15人参加的演讲比赛中,参赛选手的成绩各不相同,若选手要想知道自己是否进入前8名,只需要了解自己的成绩以及全部成绩的( )A、平均数 B、中位数 C、众数 D、以上都不对7. 如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )
A、 B、 C、 D、5. 已知x1、x2是关于x的方程x2﹣ax﹣2=0的两根,下列结论一定正确的是( )A、x1≠x2 B、x1+x2>0 C、x1•x2>0 D、x1<0,x2<06. 在只有15人参加的演讲比赛中,参赛选手的成绩各不相同,若选手要想知道自己是否进入前8名,只需要了解自己的成绩以及全部成绩的( )A、平均数 B、中位数 C、众数 D、以上都不对7. 如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( ) A、3cm B、 cm C、2.5cm D、 cm8. 如图,A,B,C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为( )
A、3cm B、 cm C、2.5cm D、 cm8. 如图,A,B,C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为( )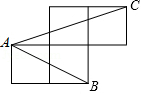 A、 B、1 C、 D、9. 抛物线y=ax2+bx+c的对称轴为直线x=﹣1,部分图象如图所示,下列判断中:
A、 B、1 C、 D、9. 抛物线y=ax2+bx+c的对称轴为直线x=﹣1,部分图象如图所示,下列判断中:①abc>0;②b2﹣4ac>0;③9a﹣3b+c=0;④若点(﹣0.5,y1),(﹣2,y2)均在抛物线上,则y1>y2;⑤5a﹣2b+c<0.其中正确的个数有( )
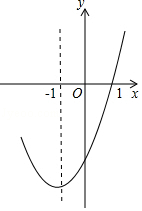 A、2 B、3 C、4 D、510.
A、2 B、3 C、4 D、510.如图是甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则( )
 A、甲、乙都可以 B、甲、乙都不可以 C、甲不可以、乙可以 D、甲可以、乙不可以
A、甲、乙都可以 B、甲、乙都不可以 C、甲不可以、乙可以 D、甲可以、乙不可以二、填空题
-
11. 计算: = .12. 写出一个满足 的整数a的值为 .13. 学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4m,AB=1.6m,CO=1m,则栏杆C端应下降的垂直距离CD为.
 14. 如图,一次函数y=﹣x﹣2与y=2x+m的图象相交于点P(n,﹣4),则关于x的不等式组 的解集为 .
14. 如图,一次函数y=﹣x﹣2与y=2x+m的图象相交于点P(n,﹣4),则关于x的不等式组 的解集为 .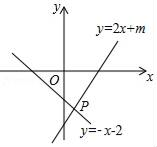 15. 刘徵是我国古代最杰出的数学家之一,他在《九算术圆田术)中用“割圆术”证明了圆面积的精确公式,并给出了计算圆周率的科学方法(注:圆周率=圆的周长与该圆直径的比值)“割圆术”就是以“圆内接正多边形的面积”,来无限逼近“圆面积”,刘徽形容他的“割圆术”说:割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣.刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径R.此时圆内接正六边形的周长为6R,如果将圆内接正六边形的周长等同于圆的周长,可得圆周率为3.当正十二边形内接于圆时,如果按照上述方法计算,可得圆周率为 . (参考数据:sinl5°=0.26)
15. 刘徵是我国古代最杰出的数学家之一,他在《九算术圆田术)中用“割圆术”证明了圆面积的精确公式,并给出了计算圆周率的科学方法(注:圆周率=圆的周长与该圆直径的比值)“割圆术”就是以“圆内接正多边形的面积”,来无限逼近“圆面积”,刘徽形容他的“割圆术”说:割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣.刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径R.此时圆内接正六边形的周长为6R,如果将圆内接正六边形的周长等同于圆的周长,可得圆周率为3.当正十二边形内接于圆时,如果按照上述方法计算,可得圆周率为 . (参考数据:sinl5°=0.26)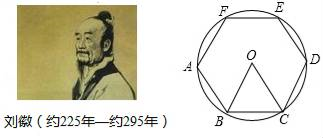
三、计算题
-
16. 先化简,再求值:(1﹣ )÷ ,其中x=2sin45°+1.
四、综合题
-
17. 老师随机抽查了本学期学生读课外书册数的情况,绘制成条形图(图1)和不完整的扇形图(图2),其中条形图被墨迹遮盖了一部分.
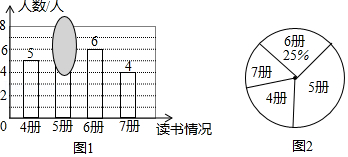 (1)、求条形图中被遮盖的数,并写出册数的中位数;(2)、在所抽查的学生中随机选一人谈读书感想,求选中读书超过5册的学生的概率;(3)、随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多补查了人.18. 已知:如图,以等边△ABC的边BC为直径作⊙O,分别交AB,AC于点D,E,过点D作DF⊥AC交AC于点F.
(1)、求条形图中被遮盖的数,并写出册数的中位数;(2)、在所抽查的学生中随机选一人谈读书感想,求选中读书超过5册的学生的概率;(3)、随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多补查了人.18. 已知:如图,以等边△ABC的边BC为直径作⊙O,分别交AB,AC于点D,E,过点D作DF⊥AC交AC于点F. (1)、求证:DF是⊙O的切线;(2)、若等边△ABC的边长为8,求由 、DF、EF围成的阴影部分面积19. 某地2015年为做好“精准扶贫”,投入资金1280万元用于异地安置,并规划投入资金逐年增加,2017年在2015年的基础上增加投入资金1600万元.(1)、从2015年到2017年,该地投入异地安置资金的年平均增长率为多少?(2)、在2017年异地安置的具体实施中,该地计划投入资金不低于500万元用于优先搬迁租房奖励,规定前1000户(含第1000户)每户每天奖励8元,1000户以后每户每天补助5元,按租房400天计算,试求今年该地至少有多少户享受到优先搬迁租房奖励?20. 如图,一次函数y=x+4的图象与反比例函数y= (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)、求证:DF是⊙O的切线;(2)、若等边△ABC的边长为8,求由 、DF、EF围成的阴影部分面积19. 某地2015年为做好“精准扶贫”,投入资金1280万元用于异地安置,并规划投入资金逐年增加,2017年在2015年的基础上增加投入资金1600万元.(1)、从2015年到2017年,该地投入异地安置资金的年平均增长率为多少?(2)、在2017年异地安置的具体实施中,该地计划投入资金不低于500万元用于优先搬迁租房奖励,规定前1000户(含第1000户)每户每天奖励8元,1000户以后每户每天补助5元,按租房400天计算,试求今年该地至少有多少户享受到优先搬迁租房奖励?20. 如图,一次函数y=x+4的图象与反比例函数y= (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C. (1)、求此反比例函数的表达式;(2)、若点P在x轴上,且S△ACP= S△BOC , 求点P的坐标.21. 如图,在边长为2的正方形 中, 为 的中点, 为边 上一动点,设 ,线段 的垂直平分线分别交边 、 于点 、 ,过 作 于点 ,过 作 于点 .
(1)、求此反比例函数的表达式;(2)、若点P在x轴上,且S△ACP= S△BOC , 求点P的坐标.21. 如图,在边长为2的正方形 中, 为 的中点, 为边 上一动点,设 ,线段 的垂直平分线分别交边 、 于点 、 ,过 作 于点 ,过 作 于点 . (1)、当 时,求证: ;(2)、顺次连接 、 、 、 ,设四边形 的面积为 ,求出 与自变量 之间的函数关系式,并求 的最小值.22. 如图,直线y=﹣ x+3与x轴交于点A,与y轴交于点B.抛物线y=﹣ x2+bx+c经过A、B两点,与x轴的另一个交点为C.
(1)、当 时,求证: ;(2)、顺次连接 、 、 、 ,设四边形 的面积为 ,求出 与自变量 之间的函数关系式,并求 的最小值.22. 如图,直线y=﹣ x+3与x轴交于点A,与y轴交于点B.抛物线y=﹣ x2+bx+c经过A、B两点,与x轴的另一个交点为C.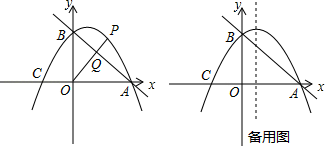 (1)、求抛物线的解析式;(2)、点P是第一象限抛物线上的点,连接OP交直线AB于点Q.设点P的横坐标为m,PQ与OQ的比值为y,求y与m的关系式,并求出PQ与OQ的比值的最大值;(3)、点D是抛物线对称轴上的一动点,连接OD、CD,设△ODC外接圆的圆心为M,当sin∠ODC的值最大时,求点M的坐标.
(1)、求抛物线的解析式;(2)、点P是第一象限抛物线上的点,连接OP交直线AB于点Q.设点P的横坐标为m,PQ与OQ的比值为y,求y与m的关系式,并求出PQ与OQ的比值的最大值;(3)、点D是抛物线对称轴上的一动点,连接OD、CD,设△ODC外接圆的圆心为M,当sin∠ODC的值最大时,求点M的坐标.
-