山东省济南市槐荫区2019年中考数学一模考试试卷
试卷更新日期:2020-04-28 类型:中考模拟
一、选择题
-
1. (﹣3)2的值是( )A、﹣9 B、9 C、﹣6 D、62. 下面是几何体中,主视图是矩形的( )A、
 B、
B、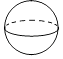 C、
C、 D、
D、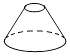 3. 下列计算正确的是( )A、a+a=a2 B、(2a)3=6a3 C、(a-1)2=a2-1 D、a3÷a=a24. 如图,一副三角尺按不同的位置摆放,下列摆放方式中∠α与∠β互余的是( )A、
3. 下列计算正确的是( )A、a+a=a2 B、(2a)3=6a3 C、(a-1)2=a2-1 D、a3÷a=a24. 如图,一副三角尺按不同的位置摆放,下列摆放方式中∠α与∠β互余的是( )A、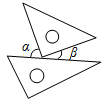 B、
B、 C、
C、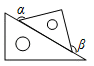 D、
D、 5. 如图,直线AB∥CD,则下列结论正确的是( )
5. 如图,直线AB∥CD,则下列结论正确的是( )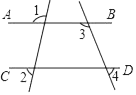 A、∠1=∠2 B、∠3=∠4 C、∠1+∠3=180° D、∠3+∠4=180°6. 分式方程 -1= 的解为( )A、x=1 B、x=-1 C、无解 D、x=-27. 不等式组 整数解的个数是( )A、 B、 C、 D、8. 已知直线y=ax+b(a≠0)经过第一,二,四象限,那么直线y=bx-a一定不经过( )
A、∠1=∠2 B、∠3=∠4 C、∠1+∠3=180° D、∠3+∠4=180°6. 分式方程 -1= 的解为( )A、x=1 B、x=-1 C、无解 D、x=-27. 不等式组 整数解的个数是( )A、 B、 C、 D、8. 已知直线y=ax+b(a≠0)经过第一,二,四象限,那么直线y=bx-a一定不经过( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 如图,由四个直角边分别是6和8的全等直角三角形拼成的“赵爽弦图”,随机往大正方形区域内投针一次,则针扎在小正方形GHEF部分的概率是( ) A、 B、 C、 D、10. 如图,在菱形 中,点 的坐标为 ,对角线 相交于点 .双曲线 经过点 ,交 的延长线于点 ,则过点 的双曲线表达式为( )
A、 B、 C、 D、10. 如图,在菱形 中,点 的坐标为 ,对角线 相交于点 .双曲线 经过点 ,交 的延长线于点 ,则过点 的双曲线表达式为( ) A、 B、 C、 D、11. 如图,矩形ABCD长与宽的比为3:2,点E , F分别在边AB、BC上,tan∠1= ,tan∠2= ,则cos(∠1+∠2)=( )
A、 B、 C、 D、11. 如图,矩形ABCD长与宽的比为3:2,点E , F分别在边AB、BC上,tan∠1= ,tan∠2= ,则cos(∠1+∠2)=( ) A、 B、 C、 D、112. 如图,抛物线y= x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C , 点Q是线段OB上一动点,连接BC , 点M在线段BC上,且使△BQM为直角三角形的同时△CQM为等腰三角形,则此时点Q的横坐标为( )
A、 B、 C、 D、112. 如图,抛物线y= x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C , 点Q是线段OB上一动点,连接BC , 点M在线段BC上,且使△BQM为直角三角形的同时△CQM为等腰三角形,则此时点Q的横坐标为( ) A、 或 B、 或 C、 或 D、 或
A、 或 B、 或 C、 或 D、 或二、填空题
-
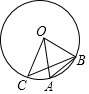
13. 3月7日~3月12日,“ 槐荫区数学文化年”标志评选活动在“勾股数学”微信公众号上进行,最终该评选页面的点击量为 次, 用科学记数法表示为 .14. 在﹣2,1,4,﹣3,0这5个数字中,任取一个数是负数的概率是 .15. 计算: .16. 如图,点A、B、C都在⊙O上,OC⊥OB,点A在劣弧 上,且OA=AB,则∠ABC= .
 17. 如图,以正六边形ABCDEF的中心O为原点建立平面直角坐标系,过点A作AP1⊥OB于点P1 , 再过P1作P1P2⊥OC于点P2 , 再过P2作P2P3⊥OD于点P3 , 依次进行……若正六边形的边长为1,则点P2019的横坐标为 .
17. 如图,以正六边形ABCDEF的中心O为原点建立平面直角坐标系,过点A作AP1⊥OB于点P1 , 再过P1作P1P2⊥OC于点P2 , 再过P2作P2P3⊥OD于点P3 , 依次进行……若正六边形的边长为1,则点P2019的横坐标为 . 18. 如图,线段AB=4,点C为线段AB上任意一点(与端点不重合),分别以AC、BC为边在AB的同侧作正方形ACDE和正方形CBGF , 分别连接BF、EG交于点M , 连接CM , 设AC=x , S四边形ACME=y , 则y与x的函数表达式为y= .
18. 如图,线段AB=4,点C为线段AB上任意一点(与端点不重合),分别以AC、BC为边在AB的同侧作正方形ACDE和正方形CBGF , 分别连接BF、EG交于点M , 连接CM , 设AC=x , S四边形ACME=y , 则y与x的函数表达式为y= .
三、计算题
-
19. 分解因式:4a2﹣9b2 .20. 计算: .
四、综合题
-
21. 如图,点 是线段 上任意一点,分别以 为边在 的同侧作等边 和等边 ,分别连接 .求证: .
 22. 有大小两种货车, 辆大货车与 辆小火车一次可以运货 吨, 辆大货车与 辆小货车一次可以运货 吨.(1)、求 辆大货车和 辆小货车一次可以分别运多少吨;(2)、现有 吨货物需要运输,货运公司拟安排大小货车共 辆把全部货物一次运完.求至少需要安排几辆大货车?23. 如图,AB是半圆O的直径,点P是BA延长线上一点,PC是⊙O的切线,切点为C,过点B作BD⊥PC交PC的延长线于点D,连接BC.求证:
22. 有大小两种货车, 辆大货车与 辆小火车一次可以运货 吨, 辆大货车与 辆小货车一次可以运货 吨.(1)、求 辆大货车和 辆小货车一次可以分别运多少吨;(2)、现有 吨货物需要运输,货运公司拟安排大小货车共 辆把全部货物一次运完.求至少需要安排几辆大货车?23. 如图,AB是半圆O的直径,点P是BA延长线上一点,PC是⊙O的切线,切点为C,过点B作BD⊥PC交PC的延长线于点D,连接BC.求证: (1)、∠PBC=∠CBD;(2)、
(1)、∠PBC=∠CBD;(2)、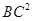 =AB•BD. 24. 某校为激发学生学习数学的兴趣,开设了“数独、速算、魔方、七巧板、华容道”五门校本课程,规定每位学生只能选一门.该校共有学生1600人.为了解学生的报名意向,学校随机调查了一些学生,并制成如下统计图表:
=AB•BD. 24. 某校为激发学生学习数学的兴趣,开设了“数独、速算、魔方、七巧板、华容道”五门校本课程,规定每位学生只能选一门.该校共有学生1600人.为了解学生的报名意向,学校随机调查了一些学生,并制成如下统计图表:校本课程报名意向统计表
课程
频数
频率
数独
8
a
速算
m
0.2
魔方
27
b
七巧板
n
0.3
华容道
15
c
 (1)、在这次活动中,学校采取的调查方式是(填写“普查”或“抽样调查”);(2)、求出扇形统计图中“速算”所对应的扇形圆心角的度数;(3)、a+b+c= , m=;(答案直接填写在横线上)(4)、请你估算,全校选择“数独”和“魔方”的学生共有多少人?25. 如图1,点A(m , 6),B(6,1)在反比例函数图象上,作直线AB , 连接OA、OB .
(1)、在这次活动中,学校采取的调查方式是(填写“普查”或“抽样调查”);(2)、求出扇形统计图中“速算”所对应的扇形圆心角的度数;(3)、a+b+c= , m=;(答案直接填写在横线上)(4)、请你估算,全校选择“数独”和“魔方”的学生共有多少人?25. 如图1,点A(m , 6),B(6,1)在反比例函数图象上,作直线AB , 连接OA、OB . (1)、求反比例函数的表达式和m的值;(2)、求△AOB的面积;(3)、如图2,E是线段AB上一点,作AD⊥x轴于点D , 过点E作x轴的垂线,交反比例函数图象于点F , 若EF= AD , 求出点E的坐标.26. 已知一个矩形纸片OACB , 将该纸片放置在平面直角坐标系中,点A(4,0),点B(0,3),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP . 设BP=t .
(1)、求反比例函数的表达式和m的值;(2)、求△AOB的面积;(3)、如图2,E是线段AB上一点,作AD⊥x轴于点D , 过点E作x轴的垂线,交反比例函数图象于点F , 若EF= AD , 求出点E的坐标.26. 已知一个矩形纸片OACB , 将该纸片放置在平面直角坐标系中,点A(4,0),点B(0,3),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP . 设BP=t . (1)、如图1,当∠BOP=30°时,求点P的坐标;(2)、如图2,经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ , 设AQ=m , 试用含有t的式子表示m;(3)、在(2)的条件下,连接OQ , 当OQ取得最小值时,求点Q的坐标;(4)、在(2)的条件下,点C′能否落在边OA上?如果能,直接写出点P的坐标;如果不能,请说明理由.27. 如图,抛物线y=ax2+bx+3与x轴交于A(﹣1,0)和B(3,0)两点,与y轴交于点C , 点D是该抛物线的顶点,分别连接AC、CD、AD .
(1)、如图1,当∠BOP=30°时,求点P的坐标;(2)、如图2,经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ , 设AQ=m , 试用含有t的式子表示m;(3)、在(2)的条件下,连接OQ , 当OQ取得最小值时,求点Q的坐标;(4)、在(2)的条件下,点C′能否落在边OA上?如果能,直接写出点P的坐标;如果不能,请说明理由.27. 如图,抛物线y=ax2+bx+3与x轴交于A(﹣1,0)和B(3,0)两点,与y轴交于点C , 点D是该抛物线的顶点,分别连接AC、CD、AD . (1)、求抛物线的函数表达式以及顶点D的坐标;(2)、在抛物线上取一点P(不与点C重合),并分别连接PA、PD , 当△PAD的面积与△ACD的面积相等时,求点P的坐标;(3)、将(1)中所求得的抛物线沿A、D所在的直线平移,平移后点A的对应点为A′,点C的对应点为C′,点D的对应点为D′,当四边形AA′C′C是菱形时,求此时平移后的抛物线的解析式.
(1)、求抛物线的函数表达式以及顶点D的坐标;(2)、在抛物线上取一点P(不与点C重合),并分别连接PA、PD , 当△PAD的面积与△ACD的面积相等时,求点P的坐标;(3)、将(1)中所求得的抛物线沿A、D所在的直线平移,平移后点A的对应点为A′,点C的对应点为C′,点D的对应点为D′,当四边形AA′C′C是菱形时,求此时平移后的抛物线的解析式.