山东省菏泽市曹县2019年中考数学三模考试试卷
试卷更新日期:2020-04-28 类型:中考模拟
一、选择题
-
1. 的结果是( )A、 B、 C、 D、2. 如图,数轴上有三个点A,B,C,若点 与 表示的数互为相反数,则点 表示数是( )
 A、 B、1 C、 D、23. 如图,将一个含有45°角的直角三角板摆放在矩形上,若∠1=35°,则∠2的度数为( )
A、 B、1 C、 D、23. 如图,将一个含有45°角的直角三角板摆放在矩形上,若∠1=35°,则∠2的度数为( )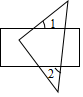 A、70° B、75° C、80° D、85°4. 关于二次函数 ,下列说法正确的是( )A、图像与 轴的交点坐标为 B、图像的对称轴在 轴的右侧 C、当 时, 的值随 值的增大而减小 D、 的最小值为-35. 如图,将平行四边形 沿对角线 折叠,使点 落在点 处, 交 于点 ,若 , ,则 的度数为( )
A、70° B、75° C、80° D、85°4. 关于二次函数 ,下列说法正确的是( )A、图像与 轴的交点坐标为 B、图像的对称轴在 轴的右侧 C、当 时, 的值随 值的增大而减小 D、 的最小值为-35. 如图,将平行四边形 沿对角线 折叠,使点 落在点 处, 交 于点 ,若 , ,则 的度数为( )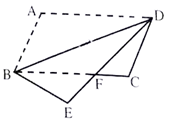 A、 B、 C、 D、6. 若直线y=kx+k﹣1经过点(m , n+3)和(m+1,2n﹣1),且0<k<2,则n的取值范围是( )A、0<n<2 B、0<n<4 C、2<n<6 D、4<n<67. 如图,四边形 中, , , , 为 的中点, 为线段 上的点,且 ,则点 到边 的距离是( )
A、 B、 C、 D、6. 若直线y=kx+k﹣1经过点(m , n+3)和(m+1,2n﹣1),且0<k<2,则n的取值范围是( )A、0<n<2 B、0<n<4 C、2<n<6 D、4<n<67. 如图,四边形 中, , , , 为 的中点, 为线段 上的点,且 ,则点 到边 的距离是( ) A、3 B、 C、4 D、8. 如图,正方形ABCD的边长为4,点P从点A出发,沿正方形的边顺时针方向运动一周,则△APC的面积y与点P运动的路程x间的函数关系图象大致是( )
A、3 B、 C、4 D、8. 如图,正方形ABCD的边长为4,点P从点A出发,沿正方形的边顺时针方向运动一周,则△APC的面积y与点P运动的路程x间的函数关系图象大致是( ) A、
A、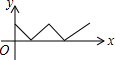 B、
B、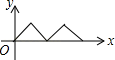 C、
C、 D、
D、
二、填空题
-
9. 若式子 在实数范围内有意义,则 的取值范围是 .10. 如图, C中, , ,将 绕点 按顺时针方向旋转后得到 ,点 恰好落在线段 上, 、 相交于 ,则 的度数为 .
 11. 观察下列关于自然数的式子: , , ,……,根据上述规律,则第2019个式子的值为 .12. 如图,四边形 是菱形, 经过点 、 、 与 相交于点 ,连接 、 ,若 ,则 的度数为 .
11. 观察下列关于自然数的式子: , , ,……,根据上述规律,则第2019个式子的值为 .12. 如图,四边形 是菱形, 经过点 、 、 与 相交于点 ,连接 、 ,若 ,则 的度数为 . 13. 如图,直线l⊥x轴于点P,且与反比例函数y1= (x>0)及y2= (x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为3,则k1﹣k2=.
13. 如图,直线l⊥x轴于点P,且与反比例函数y1= (x>0)及y2= (x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为3,则k1﹣k2=.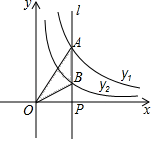 14. 如图,直线 与 轴、 轴分别交于A,B两点,C是OB的中点,D是AB上一点,四边形OEDC是菱形,则△OAE的面积为 .
14. 如图,直线 与 轴、 轴分别交于A,B两点,C是OB的中点,D是AB上一点,四边形OEDC是菱形,则△OAE的面积为 .
三、计算题
-
15. 计算:16. 解不等式组
四、综合题
-
17. 如图,平行四边形 中, 、 分别是边 、 的中点,求证: .
 18. 某商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯,如图,已知原阶梯式自动扶梯AB的长为6 m , 坡角∠ABE=45°,改造后的斜坡自动扶梯坡角∠ACB=15°,求改造后的斜坡式自动扶梯AC的长,(精确到0.1m , 参考数据;sin15°≈0.26,cos15°≈0.97,tan15°≈0,27)
18. 某商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯,如图,已知原阶梯式自动扶梯AB的长为6 m , 坡角∠ABE=45°,改造后的斜坡自动扶梯坡角∠ACB=15°,求改造后的斜坡式自动扶梯AC的长,(精确到0.1m , 参考数据;sin15°≈0.26,cos15°≈0.97,tan15°≈0,27) 19. 某商店销售某种商品,平均每天可售出20件,每件盈利40元,为了扩大销售增加盈利,该商店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件,当每件商品降价多少元时,该商品每天的销售利润为1200元?20. 如图,反比例函数y= (x>0)的图象上一点A(m , 4),过点A作AB⊥x轴于B , CD∥AB , 交x轴于C , 交反比例函数图象于D , BC=2,CD= .
19. 某商店销售某种商品,平均每天可售出20件,每件盈利40元,为了扩大销售增加盈利,该商店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件,当每件商品降价多少元时,该商品每天的销售利润为1200元?20. 如图,反比例函数y= (x>0)的图象上一点A(m , 4),过点A作AB⊥x轴于B , CD∥AB , 交x轴于C , 交反比例函数图象于D , BC=2,CD= . (1)、求反比例函数的表达式;(2)、若点P是y轴上一动点,求PA+PB的最小值.21. 某市将开展演讲比赛活动,某校对参加选拔的学生的成绩按A、B、C、D四个等级进行统计,绘制了如下不完整的统计表和扇形统计图,
(1)、求反比例函数的表达式;(2)、若点P是y轴上一动点,求PA+PB的最小值.21. 某市将开展演讲比赛活动,某校对参加选拔的学生的成绩按A、B、C、D四个等级进行统计,绘制了如下不完整的统计表和扇形统计图,成绩等级
频数
频率
A
4
n
B
m
0.51
C
D
15
 (1)、求m、n的值;(2)、求“C等级”所对应的扇形圆心角的度数;(3)、已知成绩等级为A的4名学生中有1名男生和3名女生,现从中随机挑选2名学生代表学校参加全市比赛,求出恰好选中一男生和一女生的概率22. 如图,D是 的BC边上一点,连接AD,作 的外接圆,将 沿直线AD折叠,点C的对应点E落在 的外接圆上.
(1)、求m、n的值;(2)、求“C等级”所对应的扇形圆心角的度数;(3)、已知成绩等级为A的4名学生中有1名男生和3名女生,现从中随机挑选2名学生代表学校参加全市比赛,求出恰好选中一男生和一女生的概率22. 如图,D是 的BC边上一点,连接AD,作 的外接圆,将 沿直线AD折叠,点C的对应点E落在 的外接圆上.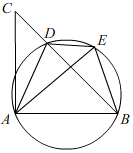 (1)、求证:AE=AB.(2)、若 , , ,求 的长.23. 在△ABC中,∠ABC=90°
(1)、求证:AE=AB.(2)、若 , , ,求 的长.23. 在△ABC中,∠ABC=90° (1)、如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为点M , N , 求证:△ABM∽△BCN;(2)、如图2,P是BC边上一点,∠BAP=∠C , tan∠PAC= ,BP=2cm , 求CP的长.24. 如图,二次函数的图象经过原点 和 ,与 轴交于另一点 ,且对称轴是 .
(1)、如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为点M , N , 求证:△ABM∽△BCN;(2)、如图2,P是BC边上一点,∠BAP=∠C , tan∠PAC= ,BP=2cm , 求CP的长.24. 如图,二次函数的图象经过原点 和 ,与 轴交于另一点 ,且对称轴是 . (1)、求二次函数的表达式;(2)、若 是 上的一点,作 ,交 于点 ,当 的面积最大时,求点 的坐标;(3)、 是 轴上的点,过 作 轴,与抛物线交于点 ,过 作 轴于 ,是否存在点 ,使以点 、 、 为顶点的三角形与以点 、 、 为顶点的三角形相似?若存在,求出点 的坐标;若不存在,请说明理由.
(1)、求二次函数的表达式;(2)、若 是 上的一点,作 ,交 于点 ,当 的面积最大时,求点 的坐标;(3)、 是 轴上的点,过 作 轴,与抛物线交于点 ,过 作 轴于 ,是否存在点 ,使以点 、 、 为顶点的三角形与以点 、 、 为顶点的三角形相似?若存在,求出点 的坐标;若不存在,请说明理由.