初中数学浙教版八年级下册第六章 反比例函数 章末检测
试卷更新日期:2020-04-28 类型:单元试卷
一、单选题
-
1. 下列函数:①y= ;②y= ;③y=﹣ ;④y=2x﹣1中,是反比例函数的有( )A、1个 B、2个 C、3个 D、4个2. 下列两个变量之间的关系为反比例关系的是( )A、匀速行驶过程中,行驶路程与时间的关系 B、体积一定时,物体的质量与密度的关系 C、质量一定时,物体的体积与密度的关系 D、长方形的长一定时,它的周长与宽的关系3. 当温度不变时,气球内气体的气压P(单位:kPa)是气体体积V(单位:m3)的函数,下表记录了一组实验数据:P与V的函数关系式可能是( )
V(单位:m3)
1
1.5
2
2.5
3
P(单位:kPa)
96
64
48
38.4
32
A、P=96V B、P=﹣16V+112 C、P=16V2﹣96V+176 D、P=4. 如图,点A、B分别是反比例函数y= 与正比例函数y=k1x,y=k2x的交点,过点A作x轴的垂线AC,垂足为C,线段AC与直线y=k2x交于点D,若△ADO的面积为4,点D为线段OB的三等分点,则k的值为( )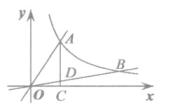 A、 B、4 C、8 D、95. 若A(m﹣1,y1),B(m+1,y2)在反比例函数 的图象上,且y1<y2 , 则m的范围是( )A、m<﹣1 B、m>1 C、﹣1<m<1 D、m<﹣1或m>16. 如图,点 在 轴正半轴上运动,点 在 轴上运动,过点 且平行于 轴的直线分别交函数 和 于 、 两点,则三角形 的面积等于( )
A、 B、4 C、8 D、95. 若A(m﹣1,y1),B(m+1,y2)在反比例函数 的图象上,且y1<y2 , 则m的范围是( )A、m<﹣1 B、m>1 C、﹣1<m<1 D、m<﹣1或m>16. 如图,点 在 轴正半轴上运动,点 在 轴上运动,过点 且平行于 轴的直线分别交函数 和 于 、 两点,则三角形 的面积等于( ) A、1 B、2 C、3 D、67. 对于反比例函数y= ,下列说法不正确的是( )A、图象分布在第一、三象限 B、当x>0时,y随x的增大而减小 C、图象经过点(2,3) D、若点A(x1 , y1),B(x2 , y2)都在图象上,且x1<x2 , 则y1<y28. 正比例函数y=2x和反比例函数 的一个交点为(1,2),则另一个交点为( )A、(﹣1,﹣2) B、(﹣2,﹣1) C、(1,2) D、(2,1)9. 已知ab<0,一次函数y=ax-b与反比例函数y= 在同一坐标系中的图象可能是( )A、
A、1 B、2 C、3 D、67. 对于反比例函数y= ,下列说法不正确的是( )A、图象分布在第一、三象限 B、当x>0时,y随x的增大而减小 C、图象经过点(2,3) D、若点A(x1 , y1),B(x2 , y2)都在图象上,且x1<x2 , 则y1<y28. 正比例函数y=2x和反比例函数 的一个交点为(1,2),则另一个交点为( )A、(﹣1,﹣2) B、(﹣2,﹣1) C、(1,2) D、(2,1)9. 已知ab<0,一次函数y=ax-b与反比例函数y= 在同一坐标系中的图象可能是( )A、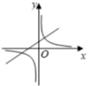 B、
B、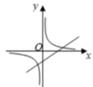 C、
C、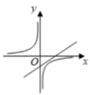 D、
D、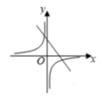 10. 如图,在平面直角坐标系中,A(-3,1),以点O为直角顶点作等腰直角三角形AOB,双曲线 在第一象限内的图象经过点B,设直线AB的解析式为 ,当 时,x的取值范围是( )
10. 如图,在平面直角坐标系中,A(-3,1),以点O为直角顶点作等腰直角三角形AOB,双曲线 在第一象限内的图象经过点B,设直线AB的解析式为 ,当 时,x的取值范围是( )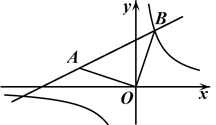 A、-5<x<1 B、0<x<1或x<-5 C、-6<x<1 D、0<x<1或x<-6
A、-5<x<1 B、0<x<1或x<-5 C、-6<x<1 D、0<x<1或x<-6二、填空题
-
11. 设函数y=x+5与y= 的的两个交点的横坐标为a、b,则 是.
12. 如图,是反比例函数y= 和y= (k1<k2)在第一象限的图象,直线AB∥x轴,并分别交两条曲线于A、B两点,若S△AOB=2,则k2﹣k1的值为 . 13. 某医药研究所开发一种新药,成年人按规定的剂量服用,服药后每毫升血液中的含药量y(毫克)与时间t(小时)之间的函数关系近似满足如图所示曲线,当每毫升血液中的含药量不少于0.5毫克时治疗有效,则服药一次治疗疾病有效的时间为小时.
13. 某医药研究所开发一种新药,成年人按规定的剂量服用,服药后每毫升血液中的含药量y(毫克)与时间t(小时)之间的函数关系近似满足如图所示曲线,当每毫升血液中的含药量不少于0.5毫克时治疗有效,则服药一次治疗疾病有效的时间为小时. 14. 若函数 是反比例函数,则 的取值是.15. 已知Rt△ABC位于第二象限,点A(﹣1,1),AB=BC=2,且两条直角边AB、BC分别平行于x轴、y轴,写出一个函数y= (k≠0),使它的图象与△ABC有两个公共点,这个函数的表达式为 .
14. 若函数 是反比例函数,则 的取值是.15. 已知Rt△ABC位于第二象限,点A(﹣1,1),AB=BC=2,且两条直角边AB、BC分别平行于x轴、y轴,写出一个函数y= (k≠0),使它的图象与△ABC有两个公共点,这个函数的表达式为 . 16. 如图,已知函数y=2x和函数 的图象交于A、B两点,过点A作AE⊥x轴于点E,若△AOE的面积为4,P是坐标平面上的点,且以点B、O、E、P为顶点的四边形是平行四边形,则满足条件的P点坐标是.
16. 如图,已知函数y=2x和函数 的图象交于A、B两点,过点A作AE⊥x轴于点E,若△AOE的面积为4,P是坐标平面上的点,且以点B、O、E、P为顶点的四边形是平行四边形,则满足条件的P点坐标是.
三、解答题
-
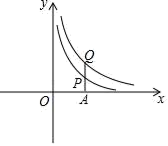
17. 反比例函数 与 在第一象限内的图象如图所示,过x轴上点A作y轴的平行线,与函数 , 的图象交点依次为P、Q两点.若PQ=2,求PA的长.
 18. 在平面直角坐标系中,一次函数y=﹣x+b的图象与反比例函数y= (k≠0)的图象交于A、B点,与y轴交于点C,其中点A的半标为(﹣2,3)
18. 在平面直角坐标系中,一次函数y=﹣x+b的图象与反比例函数y= (k≠0)的图象交于A、B点,与y轴交于点C,其中点A的半标为(﹣2,3) (1)、求一次函数和反比例函数的解析式;(2)、如图,若将点C沿y轴向上平移4个单位长度至点F,连接AF、BF,求△ABF的面积.19. 某化工车间发生有害气体泄漏,自泄漏开始到完全控制利用了40min,之后将对泄漏有害气体进行清理,线段DE表示气体泄漏时车间内危险检测表显示数据y与时间x(min)之间的函数关系(0≤x≤40),反比例函数y= 对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:
(1)、求一次函数和反比例函数的解析式;(2)、如图,若将点C沿y轴向上平移4个单位长度至点F,连接AF、BF,求△ABF的面积.19. 某化工车间发生有害气体泄漏,自泄漏开始到完全控制利用了40min,之后将对泄漏有害气体进行清理,线段DE表示气体泄漏时车间内危险检测表显示数据y与时间x(min)之间的函数关系(0≤x≤40),反比例函数y= 对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题: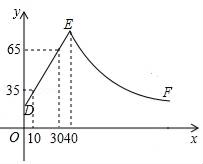 (1)、危险检测表在气体泄漏之初显示的数据是;(2)、求反比例函数y= 的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.20. 如图,奥运圣火抵达某市奥林匹克广场后,沿图中直角坐标系中的一段反比例函数图象传递.动点 表示火炬位置,火炬从离北京路10米处的M点开始传道,到离北京路1000米的N点时传递活动结束.迎圣火临时指挥部设在坐标原点O(北京路与奥运路的十字路口),OATB为少先队员鲜花方阵,方阵始终保持矩形形状且面积恒为10000(路线宽度均不计).
(1)、危险检测表在气体泄漏之初显示的数据是;(2)、求反比例函数y= 的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.20. 如图,奥运圣火抵达某市奥林匹克广场后,沿图中直角坐标系中的一段反比例函数图象传递.动点 表示火炬位置,火炬从离北京路10米处的M点开始传道,到离北京路1000米的N点时传递活动结束.迎圣火临时指挥部设在坐标原点O(北京路与奥运路的十字路口),OATB为少先队员鲜花方阵,方阵始终保持矩形形状且面积恒为10000(路线宽度均不计). (1)、求图中反比例函数的关系式(不需写出自变量的取值范围);(2)、当鲜花方阵的周长为500米时,确定此时火炬的位置(用坐标表示).21. 如图,点 在反比例函数 的图象在第二象限内的分支上, 轴于点 , 是原点,且 的面积为 .试解答下列问题:
(1)、求图中反比例函数的关系式(不需写出自变量的取值范围);(2)、当鲜花方阵的周长为500米时,确定此时火炬的位置(用坐标表示).21. 如图,点 在反比例函数 的图象在第二象限内的分支上, 轴于点 , 是原点,且 的面积为 .试解答下列问题: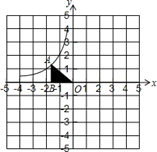 (1)、比例系数 ;(2)、在给定直角坐标系中,画出这个函数图象的另一个分支;(3)、当 时,写出 的取值范围.22. 如图,在平面直角坐标系xOy中,B(3,﹣3),C(5,0),以OC,CB为边作平行四边形OABC,函数y= (x<0)的图象经过点A.
(1)、比例系数 ;(2)、在给定直角坐标系中,画出这个函数图象的另一个分支;(3)、当 时,写出 的取值范围.22. 如图,在平面直角坐标系xOy中,B(3,﹣3),C(5,0),以OC,CB为边作平行四边形OABC,函数y= (x<0)的图象经过点A.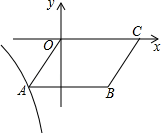 (1)、求k的值;(2)、若过点A的直线l平行于直线OB,且交函数y= (x<0)的图象于点D.
(1)、求k的值;(2)、若过点A的直线l平行于直线OB,且交函数y= (x<0)的图象于点D.①求直线l的表达式;
②定义:横、纵坐标都是整数的点叫做整点.记函数y= (x<0)的图象在点A,D之间的部分与线段AD围成的区域(含边界)为W.结合函数图象,直接写出区域W内(含边界)的整点个数.
23. 如图1,在平面直角坐标系xOy中,已知△ABC,∠ABC=90°,顶点A在第一象限内,BC在x轴的正半轴上(B在C的右侧),AB= ,∠ACB=30°,△ADC与△ABC关于AC所在的直线对称,且函数y= (k>0)的图象过点D. (1)、当OC=2时,求k的值;(2)、如图2,若点A和点D在同一个反比例函数图象上,求OC的长;(3)、在(2)的条件下,点D与点E关于原点成中心对称,x轴上有一点F,平面内有一点G,若D、E、F、G四点构成的四边形是矩形,求F点的坐标.
(1)、当OC=2时,求k的值;(2)、如图2,若点A和点D在同一个反比例函数图象上,求OC的长;(3)、在(2)的条件下,点D与点E关于原点成中心对称,x轴上有一点F,平面内有一点G,若D、E、F、G四点构成的四边形是矩形,求F点的坐标.
24. 为了预防“甲型H1N1”,某学校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题: (1)、药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?(2)、研究表明,当空气中每立方米的含药量低于1.6mg时,学生方可进教室,那么从消毒开始,至少需要几分钟后,学生才能进入教室?(3)、研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?
(1)、药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?(2)、研究表明,当空气中每立方米的含药量低于1.6mg时,学生方可进教室,那么从消毒开始,至少需要几分钟后,学生才能进入教室?(3)、研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?