初中数学浙教版八年级下册6.2 反比例函数的图象和性质（2）同步训练

试卷更新日期：2020-04-28 类型：同步测试

进入出卷网下载

一、基础夯实

1. 在平面直角坐标系中，若点（﹣2，y₁），（﹣1，y₂），（1，y₃）都在反比例函数y＝﹣ $\frac{4}{x}$ 的图象上，则y₁ ， y₂ ， y₃的大小关系是（）

A、y₃＜y₁＜y₂ B、y₃＜y₂＜y₁ C、y₁＜y₂＜y₃ D、y₁＜y₃＜y₂

查看试题解析
2. a、b是实数，点 A（2，a）、 B（3，b）在反比例函数 $y =- \frac{2}{x}$ 的图象上，则（）

A、 $a < b < 0$ B、 $b < a < 0$ C、 $a < 0 < b$ D、 $b < 0 < a$

查看试题解析
3. 在反比例函数y＝ $\frac{1 - k}{x}$ 的每一条曲线上，y都随着x的增大而减小，则k的值可以是（）

A、－1 B、1 C、2 D、3

查看试题解析
4. 若反比例函数的图象在每一象限内，y随x的增大而增大，请写出满足条件的一个反比例函数的解折式.

查看试题解析
5. 设点A（x₁ ， y₁），B(x₂ ， y₂)位于函数 $y = \frac{k}{x}$ . 的图像上，当x₁ >x₂>0必有0<y₁ <y₂ ，则k0.(选“>”，“<”，“=”中的一个填写)

查看试题解析
6. 点 $(a - 2, y_{1})$ 、 $(a + 3, y_{2})$ 在反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象上，若 $y_{1} < y_{2}$ ，则 $a$ 的取值范围是.

查看试题解析
7. 已知反比例函数 $y = \frac{k - 1}{x}$ ( $k$ 为常数, $k$ ≠1).

(1)、若点A(1,2)在这个函数的图象上,求 $k$ 的值.

(2)、若在这个函数图象的每一条分支上, $y$ 随 $x$ 的增大而减小，求 $k$ 的取值范围.

(3)、若 $k$ =13,试判断点B(3,4),C(2,5)是否在这个函数的图象上,并说明理由.

查看试题解析
8. 如图，反比例函数 $y = \frac{m - 2}{x}$ 的图象的一支在平面直角坐标系中的位置如图所示，根据图象回答下列问题：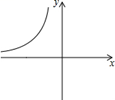

(1)、图象的另一支在第象限；在每个象限内， $y$ 随 $x$ 的增大而；

(2)、常数 $m$ 的取值范围是；

(3)、若此反比例函数的图象经过点 $(- 2 ， 3)$ ，求 $m$ 的值.点 $A (- 5 ， 2)$ 是否在这个函数图象上？点 $B (- 3 ， 4)$ 呢？

查看试题解析

二、提高特训

9. 在函数y= $\frac{- k^{2} - 2}{x}$ (k为常数)的图象上有三个点(-2，y₁)，(-1，y₂)，( $\frac{1}{2}$ ，y₃)，函数值y₁ ， y₂ ， y₃的大小为（）

A、y₁>y₂>y₃ B、y₂>y₁>y₃ C、y₂>y₃>y₁ D、y₃>y₁>y₂

查看试题解析
10. 对于反比例函数 $y = \frac{k^{2} + 1}{x}$ ，下列说法正确的个数是（）
①函数图象位于第一、三象限；②函数值 y 随 x 的增大而减小；③若 A(-1， $y_{1}$ ），B（2， $y_{2}$ ），C(1， $y_{3}$ )是图象上三个点，则 $y_{1}$ < $y_{3}$ < $y_{2}$ ；④P 为图象上任一点，过 P 作 PQ⊥y 轴于点 Q，则△OPQ 的面积是定值（）

A、1 个 B、2 个 C、3 个 D、4 个

查看试题解析
11. 已知当x＞0时，反比例函数y＝ $\frac{k}{x}$ 的函数值随自变量的增大而减小，此时关于x的方程x²﹣2（k+1）x+k²﹣1＝0的根的情况为（）

A、有两个相等的实数根 B、没有实数根 C、有两个不相等的实数根 D、无法确定

查看试题解析
12. 已知点(x₁ ， y₁)和点(x₂ ， y₂)在反比例函数y= $\frac{k}{x}$ (k<0)的图象上，若x₁<x₂ ，则（）

A、(x₁+x₂)(y₁+y₂)<0 B、(x₁+x₂)(y₁+y₂)>0 C、x₁x₂(x₁-x₂)(y₁-y₂)<0 D、x₁x₂(x₁-x₂)(y₁-y₂)>0

查看试题解析
13. 请写出一个符合以下两个条件的反比例函数的表达式：.
①图象位于第二、四象限；

②如果过图象上任意一点A作AB⊥x轴于点B，作AC⊥y轴于点C，那么得到的矩形ABOC的面积小于6.

查看试题解析
14. 已知△ABC的三个顶点为A(-1，1)，B(-1，3)，C(-3，-3)，将△ABC向右平移m(m>0)个单位后，△ABC某一边的中点恰好落在反比例函数y= $\frac{3}{x}$ 的图象上，则m的值为。

查看试题解析
15. 如图，已知点A(2，m)是反比例函数y= $\frac{k}{x}$ (k>0，x>0)的图象上一点，过点A作AB⊥x轴于点B，连结OA，△ABO的面积为4．

(1)、求k和m的值

(2)、直线y= $\frac{1}{2}$ x+n(n<0)与AB的延长线交于点C，与反比例函数图象交于点E。
①若n=-2，求点C坐标

②若点E到直线AB的距离等于AC，求n的值。

查看试题解析

初中数学浙教版八年级下册6.2 反比例函数的图象和性质（2） 同步训练

一、基础夯实

二、提高特训

初中数学浙教版八年级下册6.2 反比例函数的图象和性质（2）同步训练