2015年广西贵港市中考数学真题试卷
试卷更新日期:2016-04-22 类型:中考真卷
一、单选题(本大题共12小题,每小题3分,共36分,每小题四个选项,其中只有一个是正确的)
-
1. 3的倒数是( )A、3 B、-3 C、 D、2. 计算×的结果是( )A、 B、 C、 D、3.
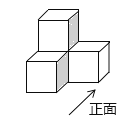
如图,是由四个完全相同的小正方形组成的立体图形,它的俯视图是( )
 A、
A、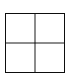 B、
B、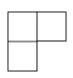 C、
C、 D、
D、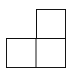 4. 下列因式分解错误的是( )A、2a﹣2b=2(a﹣b) B、x2﹣9=(x+3)(x﹣3) C、a2+4a﹣4=(a+2)2 D、﹣x2﹣x+2=﹣(x﹣1)(x+2)5. 在平面直角坐标系中,若点P(m,m﹣n)与点Q(﹣2,3)关于原点对称,则点M(m,n)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 若关于x的一元二次方程(a﹣1)x2﹣2x+2=0有实数根,则整数a的最大值为( )
4. 下列因式分解错误的是( )A、2a﹣2b=2(a﹣b) B、x2﹣9=(x+3)(x﹣3) C、a2+4a﹣4=(a+2)2 D、﹣x2﹣x+2=﹣(x﹣1)(x+2)5. 在平面直角坐标系中,若点P(m,m﹣n)与点Q(﹣2,3)关于原点对称,则点M(m,n)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 若关于x的一元二次方程(a﹣1)x2﹣2x+2=0有实数根,则整数a的最大值为( )
A、-1 B、0 C、1 D、27. 下列命题中,属于真命题的是( )A、三点确定一个圆 B、圆内接四边形对角互余 C、若a2=b2 , 则a=b D、若= , 则a=b8. 若在“正三角形、平行四边形、菱形、正五边形、正六边形”这五种图形中随机抽取一种图形,则抽到的图形属于中心对称图形的概率是( )A、 B、 C、 D、9.如图,直线AB∥CD,直线EF与AB,CD相交于点E,F,∠BEF的平分线与CD相交于点N.若∠1=63°,则∠2=( )
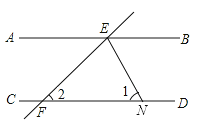 A、64° B、63° C、60° D、54°10.
A、64° B、63° C、60° D、54°10.如图,已知P是⊙O外一点,Q是⊙O上的动点,线段PQ的中点为M,连接OP,OM.若⊙O的半径为2,OP=4,则线段OM的最小值是( )
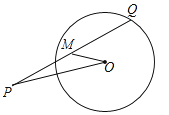 A、0 B、1 C、2 D、311.
A、0 B、1 C、2 D、311.如图,已知二次函数的图象与正比例函数的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2 , 则x的取值范围是( )
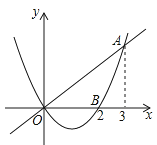 A、0<x<2 B、0<x<3 C、2<x<3 D、x<0或x>312.
A、0<x<2 B、0<x<3 C、2<x<3 D、x<0或x>312.如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=;⑤S四边形CDEF=S△ABF , 其中正确的结论有( )
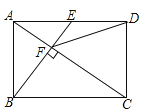 A、5个 B、4个 C、3个 D、2个
A、5个 B、4个 C、3个 D、2个二、填空题(本大题共6小题,每小题3分,共18分)
-
13. 若在实数范围内有意义,则x的取值范围是 .
14. 一种花瓣的花粉颗粒直径约为0.0000065米,将数据0.0000065用科学记数法表示为 .15. 在一次数学测试中,某班50名学生的成绩分为六组,第一组到第四组的频数分别为6,8,9,12,第五组的频率是0.2,则第六组的频数是 .16.如图,在正方形ABCD的外侧,作等边三角形CDE,连接AE,BE,则∠AEB的度数为 .
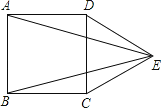 17.
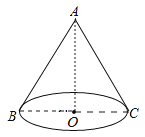
17.如图,已知圆锥的底面⊙O的直径BC=6,高OA=4,则该圆锥的侧面展开图的面积为 .
 18.
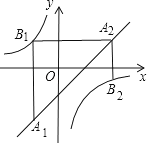
18.如图,已知点A1 , A2 , …,An均在直线y=x﹣1上,点B1 , B2 , …,Bn均在双曲线上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=﹣1,则a2015= .
三、解答题(本大题共8小题,满分66分,解答时应写出文字说明、证明过程或演算步骤)
-
19.(1)、计算:﹣2﹣1+(﹣π)0﹣|﹣2|﹣2cos30°;(2)、解不等式组 , 并在数轴上表示不等式组的解集.20.
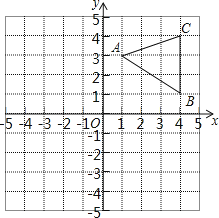
如图,已知△ABC三个顶点坐标分别是A(1,3),B(4,1),C(4,4).
 (1)、请按要求画图:
(1)、请按要求画图:①画出△ABC向左平移5个单位长度后得到的△A1B1C1;
②画出△ABC绕着原点O顺时针旋转90°后得到的△A2B2C2 .
(2)、请写出直线B1C1与直线B2C2的交点坐标.21.如图,一次函数y=x+b的图象与反比例函数y=的图象交于点A和点B(﹣2,n),与x轴交于点C(﹣1,0),连接OA.
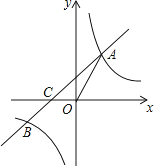 (1)、求一次函数和反比例函数的解析式;(2)、若点P在坐标轴上,且满足PA=OA,求点P的坐标.22.
(1)、求一次函数和反比例函数的解析式;(2)、若点P在坐标轴上,且满足PA=OA,求点P的坐标.22.某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如下不完整的统计图表:
乙校成绩统计表
分数(分)
人数(人)
70
7
80
90
1
100
8
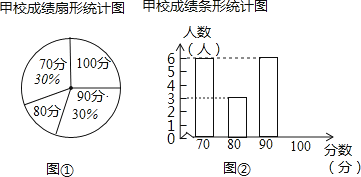 (1)、在图①中,“80分”所在扇形的圆心角度数为 ;(2)、请你将图②补充完整;(3)、求乙校成绩的平均分;(4)、经计算知S甲2=135,S乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.23. 某工厂通过科技创新,生产效率不断提高.已知去年月平均生产量为120台机器,今年一月份的生产量比去年月平均生产量增长了m%,二月份的生产量又比一月份生产量多50台机器,而且二月份生产60台机器所需要时间与一月份生产45台机器所需时间相同,三月份的生产量恰好是去年月平均生产量的2倍.
(1)、在图①中,“80分”所在扇形的圆心角度数为 ;(2)、请你将图②补充完整;(3)、求乙校成绩的平均分;(4)、经计算知S甲2=135,S乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.23. 某工厂通过科技创新,生产效率不断提高.已知去年月平均生产量为120台机器,今年一月份的生产量比去年月平均生产量增长了m%,二月份的生产量又比一月份生产量多50台机器,而且二月份生产60台机器所需要时间与一月份生产45台机器所需时间相同,三月份的生产量恰好是去年月平均生产量的2倍.问:今年第一季度生产总量是多少台机器?m的值是多少?
24.如图,已知AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E,且点E是OD的中点,⊙O的切线BM与AO的延长线相交于点M,连接AC,CM.
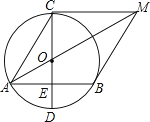 (1)、
(1)、若AB=4 , 求
 的长;(结果保留π)(2)、求证:四边形ABMC是菱形.25.
的长;(结果保留π)(2)、求证:四边形ABMC是菱形.25.如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=﹣1.
 (1)、求抛物线的解析式并写出其顶点坐标;(2)、若动点P在第二象限内的抛物线上,动点N在对称轴l上.
(1)、求抛物线的解析式并写出其顶点坐标;(2)、若动点P在第二象限内的抛物线上,动点N在对称轴l上.①当PA⊥NA,且PA=NA时,求此时点P的坐标;
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
26.已知:△ABC是等腰直角三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰直角三角形PCQ,其中∠PCQ=90°,探究并解决下列问题:
 (1)、如图①,若点P在线段AB上,且AC=1+ , PA= , 则:
(1)、如图①,若点P在线段AB上,且AC=1+ , PA= , 则:①线段PB= ,PC= ;
②猜想:PA2 , PB2 , PQ2三者之间的数量关系为 ;
(2)、如图② , 若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;(3)、若动点P满足 , 求的值.(提示:请利用备用图进行探求)