2015年广西北海市中考数学真题试卷

试卷更新日期：2016-04-22 类型：中考真卷

进入出卷网下载

一、单选题

1. ﹣2的绝对值是（　　）

A、-2 B、 $- \frac{1}{2}$ C、2 D、 $\frac{1}{2}$

查看试题解析
2. 计算2^﹣1+ $\frac{1}{2}$ 的结果是（　　）

A、0 B、1 C、2 D、 $2 \frac{1}{2}$

查看试题解析
3. 已知∠A=40°，则它的余角为（　　）

A、40° B、50° C、130° D、140°

查看试题解析
4.
一个几何体的三视图如图所示，则这个几何体是（　　）

A、圆柱 B、圆锥 C、球 D、以上都不正确

查看试题解析
5. 某市户籍人口1694000人，则该市户籍人口数据用科学记数法可表示为（　　）

A、1.694×10⁴人 B、1.694×10⁵人 C、1.694×10⁶人 D、1.694×10⁷人

查看试题解析
6. 三角形三条中线的交点叫做三角形的（　　）

A、内心 B、外心 C、中心 D、重心

查看试题解析
7.
正比例函数y=kx的图象如图所示，则k的取值范围是（　　）

A、k＞0 B、k＜0 C、k＞1 D、k＜1

查看试题解析
8. 下列运算正确的是（　　）

A、3a+4b=12a B、（ab³）²=ab⁶ C、（5a²﹣ab）﹣（4a²+2ab）=a²﹣3ab D、x¹²÷x⁶=x²

查看试题解析
9. 下列命题中，属于真命题的是（　　）

A、各边相等的多边形是正多边形 B、矩形的对角线互相垂直 C、三角形的中位线把三角形分成面积相等的两部分 D、对顶角相等

查看试题解析
10. 小强和小华两人玩“剪刀、石头、布”游戏，随机出手一次，则两人平局的概率为（　　）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
11. 下列因式分解正确的是（　　）

A、x²﹣4=（x+4）（x﹣4） B、x²+2x+1=x（x+2）+1 C、3mx﹣6my=3m（x﹣6y） D、2x+4=2（x+2）

查看试题解析
12.
如图，在矩形OABC中，OA=8，OC=4，沿对角线OB折叠后，点A与点D重合，OD与BC交于点E，则点D的坐标是（　　）

A、（4，8） B、（5，8） C、（ $\frac{24}{5}$ ， $\frac{32}{5}$ ） D、（ $\frac{22}{5}$ ， $\frac{36}{5}$ ）

查看试题解析

二、填空题

13. 9的算术平方根是．

查看试题解析
14. 在市委宣传部举办的以“弘扬社会主义核心价值观”为主题的演讲比赛中，其中9位参赛选手的成绩如下：9.3；9.5；8.9；9.3；9.5；9.5；9.7；9.4；9.5，这组数据的众数是．

查看试题解析
15. 已知点A（ $- \sqrt{2}$ ， m）是反比例函数 $y = \frac{8}{x}$ 图象上的一点，则m的值为．

查看试题解析
16.
如图，已知正方形ABCD的边长为4，对角线AC与BD相交于点O，点E在DC边的延长线上．若∠CAE=15°，则AE= ．

查看试题解析
17. 用一个圆心角为120°，半径为6的扇形作一个圆锥的侧面，这个圆锥的底面圆的半径是．

查看试题解析
18.
如图，直线y=﹣2x+2与两坐标轴分别交于A、B两点，将线段OA分成n等份，分点分别为P₁ ， P₂ ， P₃ ， …，P_n﹣1 ，过每个分点作x轴的垂线分别交直线AB于点T₁ ， T₂ ， T₃ ， …，T_n﹣1 ，用S₁ ， S₂ ， S₃ ， …，S_n﹣1分别表示Rt△T₁OP₁ ， Rt△T₂P₁P₂ ， …，Rt△T_n﹣1P_n﹣2P_n﹣1的面积，则当n=2015时，S₁+S₂+S₃+…+S_n﹣1= ．

查看试题解析

三、解答题

19. 解方程： $\frac{2}{x} = \frac{3}{x + 1}$ ．

查看试题解析
20. 解不等式组： $\{\begin{matrix} 2 x - 1 > 1 \\ x + 1 > 2 (x - 1) \end{matrix}$ ．

查看试题解析
21.
某校为了解学生对篮球、足球、排球、羽毛球、乒乓球这五种球类运动的喜爱情况，随机抽取一部分学生进行问卷调查，统计整理并绘制了以下两幅不完整的统计图：
请根据以上统计图提供的信息，解答下列问题：

(1)、共抽取名学生进行问卷调查；

(2)、补全条形统计图，求出扇形统计图中“篮球”所对应的圆心角的度数；

(3)、该校共有2500名学生，请估计全校学生喜欢足球运动的人数．

查看试题解析
22.
如图，已知BD平分∠ABF，且交AE于点D，

(1)、求作：∠BAE的平分线AP（要求：尺规作图，保留作图痕迹，不写作法）；

(2)、设AP交BD于点O，交BF于点C，连接CD，当AC⊥BD时，求证：四边形ABCD是菱形．

查看试题解析
23. 某市居民用电的电价实行阶梯收费，收费标准如下表：
一户居民每月用电量x（单位：度）
电费价格（单位：元/度）
0＜x≤200
a
200＜x≤400
b
x＞400
0.92

(1)、已知李叔家四月份用电286度，缴纳电费178.76元；五月份用电316度，缴纳电费198.56元，请你根据以上数据，求出表格中a，b的值．

(2)、六月份是用电高峰期，李叔计划六月份电费支出不超过300元，那么李叔家六月份最多可用电多少度？

查看试题解析
24.
如图，A为某旅游景区的最佳观景点，游客可从B处乘坐缆车先到达小观景平台DE观景，然后再由E处继续乘坐缆车到达A处，返程时从A处乘坐升降电梯直接到达C处，已知：AC⊥BC于C，DE∥BC，BC=110米，DE=9米，BD=60米，α=32°，β=68°，求AC的高度．（参考数据：sin32°≈0.53；cos32°≈0.85；tan32°≈0.62；sin68°≈0.93；cos68°≈0.37；tan68°≈2.48）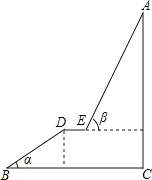

查看试题解析
25.
如图，AB、CD为⊙O的直径，弦AE∥CD，连接BE交CD于点F，过点E作直线EP与CD的延长线交于点P，使∠PED=∠C．

(1)、求证：PE是⊙O的切线；

(2)、求证：ED平分∠BEP；

(3)、若⊙O的半径为5，CF=2EF，求PD的长．

查看试题解析
26.
如图1所示，已知抛物线y=﹣x²+4x+5的顶点为D，与x轴交于A、B两点，与y轴交于C点，E为对称轴上的一点，连接CE，将线段CE绕点E按逆时针方向旋转90°后，点C的对应点C′恰好落在y轴上．

(1)、直接写出D点和E点的坐标；

(2)、点F为直线C′E与已知抛物线的一个交点，点H是抛物线上C与F之间的一个动点，若过点H作直线HG与y轴平行，且与直线C′E交于点G，设点H的横坐标为m（0＜m＜4），那么当m为何值时，S_△HGF：S_△BGF=5：6？

(3)、图2所示的抛物线是由y=﹣x²+4x+5向右平移1个单位后得到的，点T（5，y）在抛物线上，点P是抛物线上O与T之间的任意一点，在线段OT上是否存在一点Q，使△PQT是等腰直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由．

查看试题解析

一户居民每月用电量x（单位：度）	电费价格（单位：元/度）
0＜x≤200	a
200＜x≤400	b
x＞400	0.92