2015年广东省珠海市中考数学真题试卷

试卷更新日期：2016-04-22 类型：中考真卷

进入出卷网下载

一、选择题（本大题共5小题，每小题3分，共15分）

1. $\frac{1}{2}$ 的倒数是（　　）

A、 $\frac{1}{2}$ B、 $- \frac{1}{2}$ C、2 D、-2

查看试题解析
2. 计算﹣3a²×a³的结果为（　　）

A、﹣3a⁵ B、3a⁶ C、﹣3a⁶ D、3a⁵

查看试题解析
3. 一元二次方程x²+x+ $\frac{1}{4}$ =0的根的情况是（　　）

A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定根的情况

查看试题解析
4. 一次掷两枚质地均匀的硬币，出现两枚硬币都正面朝上的概率是（　　）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{1}{4}$

查看试题解析
5.
如图，在⊙O中，直径CD垂直于弦AB，若∠C=25°，则∠BOD的度数是（　　）

A、25° B、30° C、40° D、50°

查看试题解析

二、填空题（本大题共5小题，每小题4分，共20分）

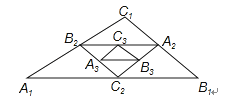
6. 若分式 $\frac{3}{x - 5}$ 有意义，则x应满足　．

查看试题解析
7. 不等式组 $\{\begin{matrix} \frac{x}{2} \geq - 1 \\ 1 - x > - 2 \end{matrix}$ 的解集是．

查看试题解析
8. 填空：x²+10x+　 =（x+　　）² ．

查看试题解析
9. 用半径为12cm，圆心角为90°的扇形纸片围成一个圆锥的侧面（接缝忽略不计），则该圆锥底面圆的半径为 cm．

查看试题解析
10.
如图，在△A₁B₁C₁中，已知A₁B₁=7，B₁C₁=4，A₁C₁=5，依次连接△A₁B₁C₁三边中点，得△A₂B₂C₂ ，再依次连接△A₂B₂C₂的三边中点得△A₃B₃C₃ ， …，则△A₅B₅C₅的周长为．

查看试题解析

三、解答题

11. 计算：﹣1²﹣ $2 \sqrt{9}$ +5⁰+|﹣3|．

查看试题解析
12. 先化简，再求值：（ $\frac{x}{x - 1}$ ﹣ $\frac{1}{x + 1}$ ）÷ $\frac{1}{x^{2} - 1}$ ，其中x= $\sqrt{2}$ ．

查看试题解析
13.
如图，在平行四边形ABCD中，AB＜BC．

(1)、利用尺规作图，在BC边上确定点E，使点E到边AB，AD的距离相等（不写作法，保留作图痕迹）；

(2)、若BC=8，CD=5，则CE= ．

查看试题解析
14.
某校体育社团在校内开展“最喜欢的体育项目（四项选一项）”调查，对九年级学生随机抽样，并将收集的数据绘制成如图两幅不完整的统计图，请结合统计
图解答下列问题：

(1)、求本次抽样人数有多少人？

(2)、补全条形统计图；

(3)、该校九年级共有600名学生，估计九年级最喜欢跳绳项目的学生有多少人？

查看试题解析
15. 白溪镇2012年有绿地面积57.5公顷，该镇近几年不断增加绿地面积，2014年达到82.8公顷．

(1)、求该镇2012至2014年绿地面积的年平均增长率；

(2)、若年增长率保持不变，2015年该镇绿地面积能否达到100公顷？

查看试题解析
16.
如图，某塔观光层的最外沿点E为蹦极项目的起跳点．已知点E离塔的中轴线AB的距离OE为10米，塔高AB为123米（AB垂直地面BC），在地面C处测得点E的仰角α=45°，从点C沿CB方向前行40米到达D点，在D处测得塔尖A的仰角β=60°，求点E离地面的高度EF．（结果精确到1米，参考数据 $\sqrt{2}$ ≈1.4， $\sqrt{3}$ ≈1.7）

查看试题解析
17. 已知抛物线y=ax²+bx+3的对称轴是直线x=1．

(1)、求证：2a+b=0

(2)、若关于x的方程ax²+bx﹣8=0的一个根为4，求方程的另一个根．

查看试题解析
18.
如图，在平面直角坐标系中，矩形OABC的顶点A，C分别在x轴，y轴上，函数y= $\frac{k}{x}$ 的图象过点P（4，3）和矩形的顶点B（m，n）（0＜m＜4）．

(1)、求k的值.

(2)、连接PA，PB，若△ABP的面积为6，求直线BP的解析式．

查看试题解析
19.
已知△ABC，AB=AC，将△ABC沿BC方向平移得到△DEF．

(1)、如图1，连接BD，AF，则BD AF（填“＞”、“＜”或“=”）；

(2)、如图2，M为AB边上一点，过M作BC的平行线MN分别交边AC，DE，DF于点G，H，N，连接BH，GF，求证：BH=GF．

查看试题解析
20.
阅读材料：善于思考的小军在解方程组时，采用了一种“整体代换”的解法：
解：将方程②变形：4x+10y+y=5 即2（2x+5y）+y=5③
把方程①代入③得：2×3+y=5，∴y=﹣1
把y=﹣1代入①得x=4，∴方程组的解为 $\{\begin{matrix} x = 4 \\ y = - 1 \end{matrix}$ ．
请你解决以下问题：

(1)、
模仿小军的“整体代换”法解方程组；

(2)、
已知x，y满足方程组
（i）求x²+4y²的值；
（ii）求 $\frac{1}{x}$ + $\frac{1}{2 y}$ 的值．

查看试题解析
21.
五边形ABCDE中，∠EAB=∠ABC=∠BCD=90°，AB=BC，且满足以点B为圆心，AB长为半径的圆弧AC与边DE相切于点F，连接BE，BD．

(1)、如图1，求∠EBD的度数；

(2)、如图2，连接AC，分别与BE，BD相交于点G，H，若AB=1，∠DBC=15°，求AG•HC的值．

查看试题解析
22.
如图，折叠矩形OABC的一边BC，使点C落在OA边的点D处，已知折痕BE= $5 \sqrt{5}$ ，且 $\frac{O D}{O E}$ = $\frac{4}{3}$ ，以O为原点，OA所在的直线为x轴建立如图所示的平面直角坐标系，抛物线l：y= $- \frac{1}{16}$ x²+ $\frac{1}{2}$ x+c经过点E，且与AB边相交于点F．

(1)、求证：△ABD∽△ODE；

(2)、若M是BE的中点，连接MF，求证：MF⊥BD；

(3)、P是线段BC上一点，点Q在抛物线l上，且始终满足PD⊥DQ，在点P运动过程中，能否使得PD=DQ？若能，求出所有符合条件的Q点坐标；若不能，请说明理由．

查看试题解析