湖北省鄂州市2016-2017学年七年级下学期数学期末考试试卷

试卷更新日期：2017-09-13 类型：期末考试

进入出卷网下载

一、选择题

1. 一个数的平方根与立方根都是它本身，这个数是（）

A、1 B、﹣1 C、0 D、±1，0

查看试题解析
2. 若a²=9， $\sqrt[3]{b}$ =﹣2，则a+b=（）

A、﹣5 B、﹣11 C、﹣5 或﹣11 D、±5或±11

查看试题解析
3. 如果a＞b，那么下列各式一定正确的是（）

A、a²＞b² B、 $\frac{a}{2} < \frac{b}{2}$ C、﹣2a＜﹣2b D、a﹣1＜b﹣1

查看试题解析
4. 实数a，b在数轴上的位置如图所示，则化简 $\sqrt{{(a - 1)}^{2}}$ ﹣ $\sqrt{{(a - b)}^{2}}$ +b的结果是（）

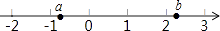A、1 B、b+1 C、2a D、1﹣2a

查看试题解析
5. 若点A（3﹣m，n+2）关于原点的对称点B的坐标是（﹣3，2），则m，n的值为（）

A、m=﹣6，n=﹣4 B、m=O，n=﹣4 C、m=6，n=4 D、m=6，n=﹣4

查看试题解析
6. 某学生某月有零花钱a元，其支出情况如图所示，那么下列说法不正确的是（）

A、该学生捐赠款为0.6a元 B、捐赠款所对应的圆心角为240° C、捐赠款是购书款的2倍 D、其他消费占10%

查看试题解析
7. 如图，四边形ABCD中，点E在AB延长线上，则下列条件中不能判断AB∥CD的是（）

A、∠3=∠4 B、∠1=∠2 C、∠5=∠C D、∠1+∠3+∠A=180°

查看试题解析
8.
如图，AB∥CD，∠1=58°，FG平分∠EFD，则∠FGB的度数等于（）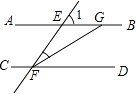

A、122° B、151° C、116° D、97°

查看试题解析
9. 如果二元一次方程ax+by+2=0有两个解 ${\begin{matrix} x = 1 \\ y = - 1 \end{matrix}$ 与 ${\begin{matrix} x = 2 \\ y = 2 \end{matrix}$ ，那么，下面四个选项中仍是这个方程的解的是（）

A、 ${\begin{matrix} x = 3 \\ y = 5 \end{matrix}$ B、 ${\begin{matrix} x = 5 \\ y = 3 \end{matrix}$ C、 ${\begin{matrix} x = 6 \\ y = 2 \end{matrix}$ D、 ${\begin{matrix} x = 4 \\ y = 4 \end{matrix}$

查看试题解析
10.
如图，矩形BCDE的各边分别平行于x轴与y轴，物体甲和物体乙由点A（2，0）同时出发，沿矩形BCDE的边作环绕运动，物体甲按逆时针方向以1个单位/秒匀速运动，物体乙按顺时针方向以2个单位/秒匀速运动，则两个物体运动后的第2018次相遇地点的坐标是（）

A、（1，﹣1） B、（2，0） C、（﹣1，1） D、（﹣1，﹣1）

查看试题解析

二、填空题

11. $\sqrt{5} - 2$ 的绝对值是．

查看试题解析
12. 如图，小章利用一张左、右两边已经破损的长方形纸片ABCD做折纸游戏，他将纸片沿EF折叠后，D、C两点分别落在D′、C′的位置，并利用量角器量得∠EFB=66°，则∠AED′等于度．

查看试题解析
13. 在平面直角坐标系中，对于点P（x，y），我们把点P′（﹣y+1，x+1）叫作点P的伴随点．已知点A₁的伴随点为A₂ ，点A₂的伴随点为A₃ ，点A₃的伴随点为A₄ ，这样依次得到点A₁ ， A₂ ， A₃ ， A₄…，若点A₁的坐标为（a，b），对于任意的正整数n，点A_n均在x轴上方，则a，b应满足的条件为．

查看试题解析
14. 若|x﹣2y+1|+|x+y﹣5|=0，则x= ， y= ．

查看试题解析
15. 小明统计了他家今年5月份打电话的次数及通话时间，并列出了频数分布表：
通话时间x/min
0＜x≤5
5＜x≤10
10＜x≤15
15＜x≤20
频数（通话次数）
20
16
9
5
则通话时间不超过10min的频率为．

查看试题解析
16. 若关于x的不等式组 ${\begin{matrix} x - a > 3 \\ 1 - 2 x > x - 2 \end{matrix}$ 无解，则a的取值范围是．

查看试题解析

三、解答题

17. 解方程组或不等式组：
① ${\begin{matrix} 2 - x > 0 \\ \frac{5 x + 1}{2} + 1 \geq \frac{2 x - 1}{3} \end{matrix}$
② ${\begin{matrix} \frac{x}{3} - \frac{y}{2} = 3 \\ \frac{x}{6} + \frac{y}{3} = 5 \end{matrix}$ ．

查看试题解析
18. 如图，A、B、C三点在同一直线上，∠1=∠2，∠3=∠D，试判断BD与CF的位置关系，并说明理由．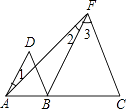

查看试题解析
19. 某校食堂的中餐与晚餐的资费标准如下：
种类
单价
米饭
0.5元/份
A类套餐菜
3.5元/份
B类套餐菜
2.5元/份
小杰同学某星期从周一到周五每天的中餐与晚餐均在学校选用A类或B类中的一份套餐菜与一份米饭用餐，这五天共消费36元．请问小杰在这五天内，A，B类套餐菜各选用了多少次？

查看试题解析
20. 为传播奥运知识，小刚就本班学生对奥运知识的了解程度进行了一次调查统计：A：熟悉，B：了解较多，C：一般了解．图1和图2是他采集数据后，绘制的两幅不完整的统计图，请你根据图中提供的信息解答以下问题：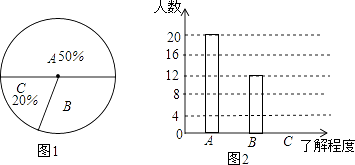

(1)、求该班共有多少名学生；

(2)、在条形图中，将表示“一般了解”的部分补充完整；

(3)、在扇形统计图中，计算出“了解较多”部分所对应的圆心角的度数；

(4)、如果全年级共1000名同学，请你估算全年级对奥运知识“了解较多”的学生人数．

查看试题解析
21.
如图，△ABC在直角坐标系中，

(1)、请写出△ABC各点的坐标．

(2)、求出△ABC的面积．

(3)、若把△ABC向上平移2个单位，再向右平移2个单位得到△A′B′C′，请在图中画出△A′B′C′，并写出点A′、B′、C′的坐标．

查看试题解析
22. 若关于x、y的二元一次方程组 ${\begin{matrix} 3 x - y = 2 a - 5 \\ x + 2 y = 3 a + 3 \end{matrix}$ 的解都为正数．

(1)、求a的取值范围；

(2)、化简|a+1|﹣|a﹣1|；

(3)、若上述二元一次方程组的解是一个等腰三角形的一条腰和一条底边的长，且这个等腰三角形的周长为9，求a的值．

查看试题解析
23. 如图1，直线MN与直线AB、CD分别交于点E、F，∠1与∠2互补．

(1)、试判断直线AB与直线CD的位置关系，并说明理由；

(2)、如图2，∠BEF与∠EFD的角平分线交于点P，EP与CD交于点G，点H是MN上一点，且GH⊥EG，求证：PF∥GH；

(3)、如图3，在（2）的条件下，连接PH，K是GH上一点使∠PHK=∠HPK，作PQ平分∠EPK，问∠HPQ的大小是否发生变化？若不变，请求出其值；若变化，说明理由．

查看试题解析
24. 我区注重城市绿化提高市民生活质量，新建林荫公园计划购买甲、乙两种树苗共800株，甲种树苗每株12元，乙种树苗每株15元．相关资料表明：甲、乙两种树苗的成活率分别为85%、90%．

(1)、若购买这两种树苗共用去10500元，则甲、乙两种树苗各购买多少株？

(2)、若要使这批树苗的总成活率不低于88%，则甲种树苗至多购买多少株？

(3)、在（2）的条件下，应如何选购树苗，使购买树苗的费用最低？并求出最低费用．

查看试题解析

通话时间x/min	0＜x≤5	5＜x≤10	10＜x≤15	15＜x≤20
频数（通话次数）	20	16	9	5

种类	单价
米饭	0.5元/份
A类套餐菜	3.5元/份
B类套餐菜	2.5元/份