云南省临沧市2016-2017学年八年级下学期数学期末考试试卷
试卷更新日期：2017-09-13 类型：期末考试
一、填空题
-
1. 据统计，全球每分钟约有8500000吨污水排入江河湖海，将8500000用科学记数法表示为吨．2. 甲、乙两人进行射击测试，每人20次射击成绩的平均数都是8.5环，方差分别是：S甲2=3，S乙2=2.5，则射击成绩较稳定的是（填“甲”或“乙”）．3. 已知，如图，直线AB与CD相交于点O，OE平分∠AOC，若∠EOC=25°，则∠BOD的度数为 ．
4. 计算： ÷（x﹣ ）= ．5. 菱形的两条对角线长分别为16和12，则菱形的周长为 ．6. （ +1）（ ﹣1）+ ﹣（ ﹣1）2= ．二、选择题
-
7. ﹣2的相反数是（ ）A、﹣ B、 C、﹣2 D、28. 要使分式 有意义，则实数x的取值范围是（ ）A、x≠6 B、x≠﹣6 C、x≥﹣6 D、x＞﹣69. 下列运算正确的是（ ）A、（a+b）（a﹣b）=a2﹣b2 B、（2a2）3=6a6 C、a6÷a2=a3 D、﹣1﹣1=010. 不等式组 的解集在数轴上表示为 （ ）A、
B、
C、
D、
11. 下列各组数中能作为直角三角形的三边长的是（ ）A、1，2，3 B、3，4，5 C、4，5，6 D、7，8，912. 下列说法错误的是（ ）A、对角线互相垂直的四边形是菱形 B、对角线互相垂直平分且相等的四边形是正方形 C、对角线相等的平行四边形是矩形 D、一组对边平行，一组对角相等的四边形是平行四边形13. 小王参加某企业招聘测试，他的笔试、面试、技能操作得分分别为85分、80分、90分，若依次按照2：3：5的比例确定成绩，则小王的成绩是（ ）A、255分 B、84分 C、84.5分 D、86分14. 一次函数y=（m﹣3）x﹣m的图象经过一、二、四象限，则m的取值范围是（ ）
A、m＜0 B、m＜3 C、0＜m＜3 D、m＞0三、解答题
-
15. 计算：（﹣1）2017﹣|﹣4|+（﹣ ）﹣2+（ ﹣3）0 ．16. 如图，AB∥CD，AB=CD，点E、F在直线BD上，BE=DF，求证：AF=CE．
17. 如图，△ABC中，∠B=90°，AB=3，BC=4，若CD=12，AD=13．求阴影部分的面积．
18.市政府决定对市直机关500户家庭的用水情况作一次调查，调查小组随机抽查了其中的100户家庭一年的月平均用水量（单位：吨），并将调查结果制成了如图所示的条形统计图．
(1)、请将条形统计图补充完整；(2)、求这100个样本数据的平均数，众数和中位数．19. 如图，正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A（m，2），一次函数图象经过点B（﹣2，﹣1），与y轴的交点为C，与x轴的交点为D．
(1)、求一次函数的解析式；(2)、求C点的坐标；(3)、求△AOD的面积；(4)、直接写出不等式kx+b＜0的解集 ．20. 已知：如图，D是△ABC的边AB上一点，CN∥AB，DN交AC于点M，若MA=MC，∠BAN=90°，求证：四边形ADCN是矩形．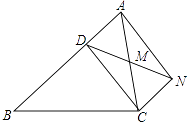
21. 甲开车从距离B市100千米的A市出发去B市，乙从同一路线上的C市出发也去往B市，二人离A市的距离与行驶时间的函数图象如图（y代表距离，x代表时间）．
(1)、C市离A市的距离是千米；(2)、甲的速度是千米∕小时，乙的速度是千米∕小时；(3)、小时，甲追上乙；(4)、试分别写出甲、乙离开A市的距离y（千米）与行驶时间x（时）之间的函数关系式．（注明自变量的范围）
