陕西省榆林市府谷县2016-2017学年八年级下学期数学期末考试试卷
试卷更新日期:2017-09-13 类型:期末考试
一、选择题
-
1. 若a>b,则下列各式中一定成立的是( )A、a+2<b+2 B、a﹣2<b﹣2 C、 > D、﹣2a>﹣2b2. 下列图案中既是中心对称图形,又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、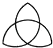 3. 把多项式x2﹣8x+16分解因式,结果正确的是( )
3. 把多项式x2﹣8x+16分解因式,结果正确的是( )
A、(x﹣4)2 B、(x﹣8)2 C、(x+4)(x﹣4) D、(x+8)(x﹣8)4. 不等式组 的解集在数轴上表示为( )A、 B、
B、 C、
C、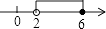 D、
D、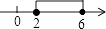 5. 如图,AD是△ABC角平分线,DE⊥AB,DF⊥AC,垂足分别为点E和点F,则下列结论正确的是( )
5. 如图,AD是△ABC角平分线,DE⊥AB,DF⊥AC,垂足分别为点E和点F,则下列结论正确的是( )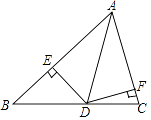 A、BD=CD B、AD=BD C、AD=CD D、DE=DF6. 小华早上从家里去离家5千米的学校,今天比昨天每小时快了1千米,结果比昨天早到了15分钟,设小华昨天每小时行x千米,可列方程( )A、 B、 C、 D、7. 在▱ABCD中,∠ACB=25°,现将▱ABCD沿EF折叠,使点C与点A重合,点D落在G处,则∠GFE的度数( )
A、BD=CD B、AD=BD C、AD=CD D、DE=DF6. 小华早上从家里去离家5千米的学校,今天比昨天每小时快了1千米,结果比昨天早到了15分钟,设小华昨天每小时行x千米,可列方程( )A、 B、 C、 D、7. 在▱ABCD中,∠ACB=25°,现将▱ABCD沿EF折叠,使点C与点A重合,点D落在G处,则∠GFE的度数( ) A、135° B、120° C、115° D、100°8. 一次函数y=kx+b(k≠0)的图象经过点B(2,0),C(0,6)两点,则kx+b≥2x的解集是( )A、x≤ B、x<2 C、x D、x≤29. 如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=( )
A、135° B、120° C、115° D、100°8. 一次函数y=kx+b(k≠0)的图象经过点B(2,0),C(0,6)两点,则kx+b≥2x的解集是( )A、x≤ B、x<2 C、x D、x≤29. 如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=( )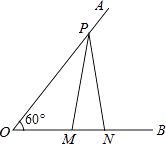 A、3 B、4 C、5 D、610. 如图,将△ABC沿直线AB翻折后得到△ABC1 , 再将△ABC绕点A旋转后得到△AB2C2 , 对于下列两个结论:
A、3 B、4 C、5 D、610. 如图,将△ABC沿直线AB翻折后得到△ABC1 , 再将△ABC绕点A旋转后得到△AB2C2 , 对于下列两个结论: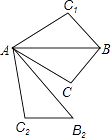
①“△ABC1能绕一点旋转后与△AB2C2重合”;
②“△ABC1能沿一直线翻折后与△AB2C2重合”的正确性是( )
A、结论①、②都正确 B、结论①、②都错误 C、结论①正确、②错误 D、结论①错误、②正确二、填空题
-
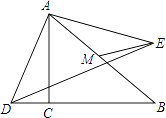
11. 分解因式:4a2﹣b2= .12. 化简: • = .13. 若关于x的不等式﹣2x+a≥2的解集是x≤﹣1,则a的值是 .14. 如图,在△ABC中,∠ACB=90°,BC=AC=4,M为AB中点,D是射线BC上的一动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接ED、ME,点D在运动过程中ME的最小值为 .
三、解答题
-
15. 计算:(1)、因式分解:2m2n﹣8mn+8n.(2)、解不等式组 .16. 解方程:1﹣ = .17.
如图,在小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,根据图形解答下列问题:

①将△ABC向左平移4个单位长度,再向下平移2个单位长度,画出平移后的△A1B1C1;
②将△DEF绕D点逆时针旋转90°,画出旋转后的△DE1F1 .
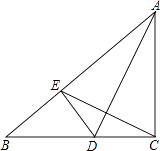
18.如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.
求证:直线AD是线段CE的垂直平分线.
 19. 潼南绿色无公害蔬菜基地有甲、乙两种植户,他们种植了A、B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
19. 潼南绿色无公害蔬菜基地有甲、乙两种植户,他们种植了A、B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:种植户
种植A类蔬菜面积
(单位:亩)
种植B类蔬菜面积
(单位:亩)
总收入
(单位:元)
甲
3
1
12500
乙
2
3
16500
说明:不同种植户种植的同类蔬菜每亩平均收入相等.
(1)、求A、B两类蔬菜每亩平均收入各是多少元?(2)、某种植户准备租20亩地用来种植A、B两类蔬菜,为了使总收入不低于63000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案.20. 综合:(1)、在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,试探究图1中线段BE、EF、FD之间的数量关系.小亮同学认为:延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,则可得到BE、EF、FD之间的数量关系.请你按照小亮的思路写出推理过程.
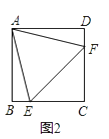
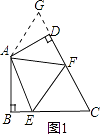 (2)、如图2,已知正方形ABCD,△AEF是正方形ABCD的内接等边三角形,请你找出S△ABE、S△ADF、S△CEF之间的数量关系,并说明理由.
(2)、如图2,已知正方形ABCD,△AEF是正方形ABCD的内接等边三角形,请你找出S△ABE、S△ADF、S△CEF之间的数量关系,并说明理由.