山东省临沂市蒙阴县2016-2017学年八年级下学期数学期末考试试卷

试卷更新日期：2017-09-13 类型：期末考试

进入出卷网下载

一、选择题

1. 下列计算错误的是（）

A、 $\sqrt{14} \times \sqrt{7} = 7 \sqrt{2}$ B、 $\sqrt{60} \div \sqrt{5} = 2 \sqrt{3}$ C、 $\sqrt{9 a} + \sqrt{25 a} = 8 \sqrt{a}$ D、 $3 \sqrt{2} - \sqrt{2} = 3$

查看试题解析
2. 下列四组线段中，可以构成直角三角形的是（　　）

A、4，5，6 B、1.5，2，2.5 C、2，3，4 D、1， $\sqrt{2}$ ， 3

查看试题解析
3. 实验学校九年级一班十名同学定点投篮测试，每人投篮六次，投中的次数统计如下：5，4，3，5，5，2，5，3，4，1，则这组数据的中位数，众数分别为（　　）

A、4，5 B、5，4 C、4，4 D、5，5

查看试题解析
4. 下列点不在正比例函数y=﹣2x的图象上的是（）

A、（5，﹣10） B、（2，﹣1） C、（0，0） D、（1，﹣2）

查看试题解析
5. 2022年将在北京﹣张家口举办冬季奥运会，很多学校开设了相关的课程．如表记录了某校4名同学短道速滑选拔赛成绩的平均数 $\bar{x}$ 与方差s²：
队员1
队员2
队员3
队员4
平均数 $\bar{x}$ （秒）
51
50
51
50
方差s²（秒²）
3.5
3.5
14.5
15.5
根据表中数据，要从中选择一名成绩好又发挥稳定的运动员参加比赛，应该选择（）

A、队员1 B、队员2 C、队员3 D、队员4

查看试题解析
6.
如图，平行四边形ABCD的对角线AC、BD相交于点O，若AC+BD=10，BC=4，则△BOC的周长为（）

A、8 B、9 C、10 D、14

查看试题解析
7.
如图是一次函数y=kx+b的图象，则k、b的符号是（）

A、k＞0，b＜0 B、k＜0，b＞0 C、k＜0，b＜0 D、k＞0，b＞0

查看试题解析
8. 若x≤0，则化简|1﹣x|﹣ $\sqrt{x^{2}}$ 的结果是（）

A、1﹣2x B、2x﹣1 C、﹣1 D、1

查看试题解析
9. 如图，在平行四边形ABCD中，∠BAD的平分线交BC于点E，∠ABC的平分线交AD于点F．若BF=12，AB=10，则AE的长为（）

A、10 B、12 C、16 D、18

查看试题解析
10. 一个有进水管与出水管的容器，从某时刻开始4min内只进水不出水，在随后的8min内既进水又出水，每分钟的进水量和出水量是两个常数，容器内的水量y（单位：L）与时间x（单位：min）之间的关系如图所示．则8min时容器内的水量为（）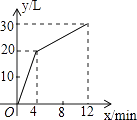

A、20 L B、25 L C、27L D、30 L

查看试题解析
11. 直线y=﹣2x+m与直线y=2x﹣1的交点在第四象限，则m的取值范围是（）

A、m＞﹣1 B、m＜1 C、﹣1＜m＜1 D、﹣1≤m≤1

查看试题解析
12.
如图，在△ABC中，AC=BC，有一动点P从点A出发，沿A→C→B→A匀速运动．则CP的长度s与时间t之间的函数关系用图象描述大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

13. 函数y= $\frac{\sqrt{x + 2}}{x - 1}$ 中自变量x的取值范围是．

查看试题解析
14. 将直线y=2x向下平移2个单位，所得直线的函数表达式是．

查看试题解析
15. 计算： $2 \sqrt{75} - 3 \sqrt{27} + \sqrt{3}$ = ．

查看试题解析
16. 数据x₁ ， x₂ ， x₃ ， x₄的平均数是4，方差是3，则数据x₁+1，x₂+1，x₃+1，x₄+1的平均数和方差分别是．

查看试题解析
17.
如图，在平面直角坐标系中，矩形ABCO的边CO、OA分别在x轴、y轴上，点E在边BC上，将该矩形沿AE折叠，点B恰好落在边OC上的F处．若OA=8，CF=4，则点E的坐标是．

查看试题解析
18. 两条平行线间的距离公式
一般地；两条平行线l₁：Ax+By+C₁=0和l₂：Ax+By+C₂=0间的距离公式是d= $\frac{| C_{1} - C_{2} |}{\sqrt{A^{2} + B^{2}}}$ 如：求：两条平行线x+3y﹣4=0和2x+6y﹣9=0的距离．
解：将两方程中x，y的系数化成对应相等的形式，得2x+6y﹣8=0和2x+6y﹣9=0，因此，d= $\frac{| - 8 + 9 |}{\sqrt{2^{2} + 6^{2}}} = \frac{\sqrt{10}}{20}$ 两条平行线l₁：3x+4y=10和l₂：6x+8y﹣10=0的距离是．

查看试题解析

三、解答题

19. 计算：| $\sqrt{2}$ ﹣3|﹣ $\sqrt{16}$ +（ $\frac{1}{3}$ ）⁰ ．

查看试题解析
20. 如图，在▱ABCD中，E、F分别是AB、DC边上的点，且AE=CF，

(1)、求证：△ADE≌△CBF．

(2)、若∠DEB=90°，求证：四边形DEBF是矩形．

查看试题解析
21.
某商场服装部为了解服装的销售情况，统计了每位营业员在某月的销售额（单位：万元），并根据统计的这组数据，绘制出如下的统计图①和图②．请根据相关信息，解答下列问题．

(1)、该商场服装部营业员的人数为，图①中m的值为

(2)、求统计的这组销售额额数据的平均数、众数和中位数．

查看试题解析
22. 某工厂现有甲种原料360千克，乙种原料290千克，计划利用这两种原料生产A、B两种产品共50件．已知生产一件A种产品，需用甲种原料9千克、乙种原料3千克，可获利润700元；生产一件B种产品，需用甲种原料4千克、乙种原料10千克，可获利润1200元．设生产A种产品的生产件数为x，A、B两种产品所获总利润为y（元）．

(1)、试写出y与x之间的函数关系式；

(2)、求出自变量x的取值范围；

(3)、利用函数的性质说明哪种生产方案获总利润最大？最大利润是多少？

查看试题解析
23. 如图，在矩形ABCD中，点E在边CD上，将该矩形沿AE折叠，使点D落在边BC上的点F处，过点F作分、FG∥CD，交AE于点G连接DG．

(1)、求证：四边形DEFG为菱形；

(2)、若CD=8，CF=4，求 $\frac{C E}{D E}$ 的值．

查看试题解析
24. 如图，在平面直角坐标系xOy中，直线y=﹣2x+a与y轴交于点C （0，6），与x轴交于点B．

(1)、求这条直线的解析式；

(2)、直线AD与（1）中所求的直线相交于点D（﹣1，n），点A的坐标为（﹣3，0）．
①求n的值及直线AD的解析式；
②求△ABD的面积；
③点M是直线y=﹣2x+a上的一点（不与点B重合），且点M的横坐标为m，求△ABM的面积S与m之间的关系式．

查看试题解析
25. 综合：

(1)、
如图1，纸片▱ABCD中，AD=5，S_▱_ABCD=15，过点A作AE⊥BC，垂足为E，沿AE剪下△ABE，将它平移至△DCE'的位置，拼成四边形AEE'D，则四边形AEE'D的形状为

A、平行四边形 B、菱形 C、矩形 D、正方形

(2)、
如图2，在（1）中的四边形纸片AEE'D中，在EE'上取一点F，使EF=4，剪下△AEF，剪下△AEF，将它平移至△DE'F'的位置，拼成四边形AFF'D．
①求证：四边形AFF'D是菱形；
②求四边形AFF'D的两条对角线的长．

查看试题解析

	队员1	队员2	队员3	队员4
平均数 $\bar{x}$ （秒）	51	50	51	50
方差s²（秒²）	3.5	3.5	14.5	15.5