内蒙古通辽市2016-2017学年八年级下学期数学期末考试试卷
试卷更新日期:2017-09-13 类型:期末考试
一、选择题
-
1. 化简: =( )A、8 B、﹣8 C、﹣4 D、42. 在下列命题中,正确的是( )A、一组对边平行的四边形是平行四边形 B、有一个角是直角的四边形是矩形 C、有一组邻边相等的平行四边形是菱形 D、对角线互相垂直平分的四边形是正方形3. 已知一次函数y=x+b的图象经过第一、三、四象限,则b的值可以是( )A、﹣1 B、0 C、1 D、24. 某个公司有15名工作人员,他们的月工资情况如表.则该公司所有工作人员的月工资的平均数、中位数和众数分别是( )
职务
经理
副经理
职员
人数
1
2
12
月工资(元)
5 000
2 000
800
A、520,2 000,2 000 B、2 600,800,800 C、1 240,2 000,800 D、1 240,800,8005. 若菱形的周长为8,高为1,则菱形两邻角的度数比为( )A、3:1 B、4:1 C、5:1 D、6:16. 一次函数y=(k﹣3)x+2,若y随x的增大而增大,则k的值可以是( )A、1 B、2 C、3 D、47. 若 在实数范围内有意义,则x的取值范围是( )A、x<3 B、x≤3 C、x>3 D、x≥38. 下列计算结果正确的是( )A、 + = B、3 ﹣ =3 C、 × = D、 =59. 如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )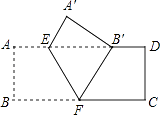 A、12 B、24 C、12 D、1610. 爷爷每天坚持体育锻炼,某天他慢跑离家到中山公园,打了一会儿太极拳后搭公交车回家.下面能反映当天小华的爷爷离家的距离y与时间x的函数关系的大致图象是( )A、
A、12 B、24 C、12 D、1610. 爷爷每天坚持体育锻炼,某天他慢跑离家到中山公园,打了一会儿太极拳后搭公交车回家.下面能反映当天小华的爷爷离家的距离y与时间x的函数关系的大致图象是( )A、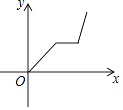 B、
B、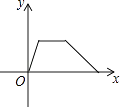 C、
C、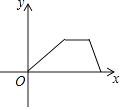 D、
D、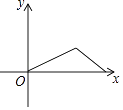
二、填空题:
-
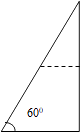
11. 若 是整数,则正整数n的最小值为 .12. 一次函数y=2x+3的图象沿y轴向下平移2个单位,所得图象的函数解析式是 .13. 随机从甲、乙两块试验田中各抽取100株麦苗测量高度,计算平均数和方差的结果为: =13, =13,S甲2=7.5,S乙2=21.6,则小麦长势比较整齐的试验田是(填“甲”或“乙”).14. 如图所示,有一张一个角为60°的直角三角形纸片,沿其一条中位线剪开后,不能拼成的四边形是 .
 15. 点(﹣2,y1),(﹣1,y2),(1,y3)都在直线y=﹣3x+b上,则y1 , y2 , y3的大小关系是 .
15. 点(﹣2,y1),(﹣1,y2),(1,y3)都在直线y=﹣3x+b上,则y1 , y2 , y3的大小关系是 .
16. 如图,一棵大树在离地面9米高的B处断裂,树顶A落在离树底BC的12米处,则大树断裂之前的高度为米. 17. 我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1 , S2 , S3 , 若S1+S2+S3=10,则S2的值是 .
17. 我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1 , S2 , S3 , 若S1+S2+S3=10,则S2的值是 .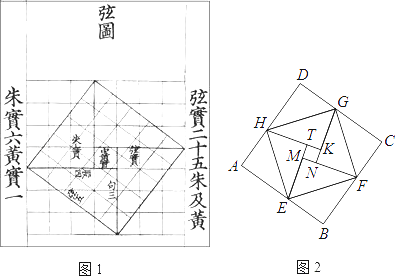
三、解答题:
-
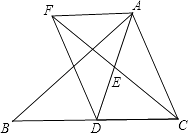
18. 计算.(1)、4 ﹣ ;(2)、(3 ﹣2 + )÷2 .19. 我们学习了四边形和一些特殊的四边形,如图表示了在某种条件下它们之间的关系.如果①,②两个条件分别是:①两组对边分别平行;②有且只有一组对边平行.那么请你对标上的其他6个数字序号写出相对应的条件.
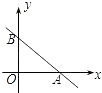
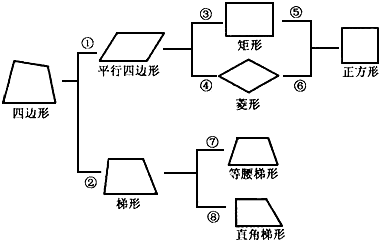 20. 如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).
20. 如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).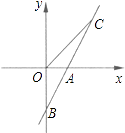 (1)、求直线AB的解析式;(2)、若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.21. 如图,某游泳池长48米,小方和小杨进行游泳比赛,从同一处(A点)出发,小方平均速度为3米/秒,小杨为3.1米/秒.但小杨一心想快,不看方向沿斜线(AC方向)游,而小方直游(AB方向),两人到达终点的位置相距14米.按各人的平均速度计算,谁先到达终点,为什么?
(1)、求直线AB的解析式;(2)、若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.21. 如图,某游泳池长48米,小方和小杨进行游泳比赛,从同一处(A点)出发,小方平均速度为3米/秒,小杨为3.1米/秒.但小杨一心想快,不看方向沿斜线(AC方向)游,而小方直游(AB方向),两人到达终点的位置相距14米.按各人的平均速度计算,谁先到达终点,为什么?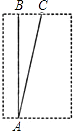 22. 如图,矩形ABCD中,O是AC与BD的交点,过O点的直线EF与AB,CD的延长线分别交于E,F.
22. 如图,矩形ABCD中,O是AC与BD的交点,过O点的直线EF与AB,CD的延长线分别交于E,F.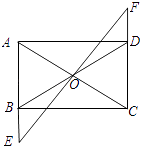 (1)、求证:△BOE≌△DOF;(2)、当EF与AC满足什么关系时,以A,E,C,F为顶点的四边形是菱形?证明你的结论.23. 甲、乙两校参加区教育局举办的学生英语口语竞赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表.
(1)、求证:△BOE≌△DOF;(2)、当EF与AC满足什么关系时,以A,E,C,F为顶点的四边形是菱形?证明你的结论.23. 甲、乙两校参加区教育局举办的学生英语口语竞赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表.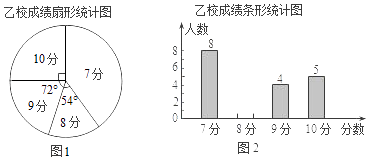
甲校成绩统计表
分数
7分
8分
9分
10分
人数
11
0
8
(1)、在图1中,“7分”所在扇形的圆心角等于°.(2)、请你将图2的统计图补充完整;(3)、经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好.(4)、如果该教育局要组织8人的代表队参加市级团体赛,为便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?