辽宁省鞍山市2016-2017学年八年级下学期数学期末考试试卷
试卷更新日期:2017-09-13 类型:期末考试
一、选择题
-
1. 在函数y=2x图象上的点是( )
A、(2,1) B、(﹣2,1) C、(1,﹣2) D、(﹣1,﹣2)2. 下列二次根式可以与 合并的是( )A、 B、 C、 D、3. 直角三角形的两条直角边长分别为4和6,那么斜边长是( )A、2 B、2 C、52 D、4. 正方形具有而矩形没有的性质是( )A、对角线互相平分 B、对边相等 C、对角线相等 D、每条对角线平分一组对角5. 如果直线y=kx+b经过一、二、四象限,则k,b的取值分别是( )A、k>0,b>0 B、k>0,b<0 C、k<0,b>0 D、k<0,b<06. 如图,菱形ABCD的对角线AC=5,BD=10,则该菱形的面积为( )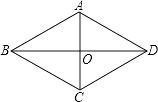 A、50 B、25 C、 D、12.57. 在数学竞赛的选拔活动中,对甲、乙两名同学的成绩经过统计分析可得: =94(分), =94(分);S =1.02,S =0.85,下列结论正确的是( )A、甲的成绩比乙的成绩好 B、甲的成绩比乙的成绩稳定 C、应该选择乙同学参加竞赛 D、不能衡量两名同学的成绩优劣8. 如图,函数y=2x和y=ax+4的图象相交于点A( ,3),则不等式2x<ax+4的解集为( )
A、50 B、25 C、 D、12.57. 在数学竞赛的选拔活动中,对甲、乙两名同学的成绩经过统计分析可得: =94(分), =94(分);S =1.02,S =0.85,下列结论正确的是( )A、甲的成绩比乙的成绩好 B、甲的成绩比乙的成绩稳定 C、应该选择乙同学参加竞赛 D、不能衡量两名同学的成绩优劣8. 如图,函数y=2x和y=ax+4的图象相交于点A( ,3),则不等式2x<ax+4的解集为( ) A、x< B、x<3 C、x> D、x>39. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点,则下列结论不正确的是( )
A、x< B、x<3 C、x> D、x>39. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点,则下列结论不正确的是( ) A、AE=CE B、CD=DE C、∠DCA=60° D、∠DEC=45°10.
A、AE=CE B、CD=DE C、∠DCA=60° D、∠DEC=45°10.如图,在矩形ABCD中,动点P从点A开始沿A→B→C→D的路径匀速运动到点D为止,在这个过程中,下列图象可以大致表示△APD的面积S随点P的运动时间t的变化关系的是( )
 A、
A、 B、
B、 C、
C、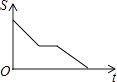 D、
D、
二、填空题
-
11. 化简:( +2)( ﹣2)= .12. 如图,在▱ABCD中,AC,BD相交于点O,点E是BC边上的中点,且OE=2cm,则边CD的长是 cm.
 13. 在△ABC中,AB=12,AC=20,BC=16,则△ABC的面积是 .14. 某公司销售一组共有10名员工,每月所创利润如下表所示:
13. 在△ABC中,AB=12,AC=20,BC=16,则△ABC的面积是 .14. 某公司销售一组共有10名员工,每月所创利润如下表所示:月利润(万元)
1
2
3
4
人数
2
4
3
1
则这个销售小组每人所创月利润平均是万元.
15. 如图,是一个正比例函数的图象,把该图象向左平移一个单位长度,得到的函数图象的解析式为 . 16. 已知x+y=﹣2,xy=3,则代数式 + 的值是 .17. 某农户种植一种经济作物,总用水量y(米3)与种植时间x(天)之间的函数关系如图所示,当总用水量为2500米3时,该经济作物种植时间是天.
16. 已知x+y=﹣2,xy=3,则代数式 + 的值是 .17. 某农户种植一种经济作物,总用水量y(米3)与种植时间x(天)之间的函数关系如图所示,当总用水量为2500米3时,该经济作物种植时间是天. 18. 如图,四边形ABCD是矩形纸片,AB=2,对折矩形纸片ABCD,使AD与BC重合,折痕为MN,展平后再过点B折叠矩形纸片,使点A落在MN上的点G处,折痕BE与MN相交于点H;再次展平,连接BG,EG,延长EG交BC于点F.有如下结论:
18. 如图,四边形ABCD是矩形纸片,AB=2,对折矩形纸片ABCD,使AD与BC重合,折痕为MN,展平后再过点B折叠矩形纸片,使点A落在MN上的点G处,折痕BE与MN相交于点H;再次展平,连接BG,EG,延长EG交BC于点F.有如下结论:①EG=FG;②∠ABG=60°;③AE=1;④△BEF是等边三角形;其中正确结论的序号是 .

三、解答题
-
19. 计算:( + )÷ +(2﹣ )2 .20. 如图,矩形ABCD的对角线AC,BD相交于点O,∠ACB=30°,BC=3,分别过点B,C作BE∥AC,CE∥BD,且BE,CE相交于点E.
 (1)、求AB,AC的长;(2)、判断四边形BOCE的形状.21. 如图,在平面直角坐标系中,点M(14,0)是x轴上的点,点P的坐标是(9,12),连接OP,PM.
(1)、求AB,AC的长;(2)、判断四边形BOCE的形状.21. 如图,在平面直角坐标系中,点M(14,0)是x轴上的点,点P的坐标是(9,12),连接OP,PM. (1)、求线段PM的长;(2)、在第一象限内找一点N,使四边形OPNM是平行四边形,画出图形并求出点N的坐标(保留作图痕迹)22.
(1)、求线段PM的长;(2)、在第一象限内找一点N,使四边形OPNM是平行四边形,画出图形并求出点N的坐标(保留作图痕迹)22.某中学七、八年级各选派10名选手参加学校举办的知识竞赛,竞赛计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下所示.
队别
平均分
众数
中位数
方差
合格率
优秀率
七年级
6.7
a
m
3.41
90%
20%
八年级
7.1
p
q
1.69
80%
10%
 (1)、请依据图表中的数据,求出a的值;并直接写出表格中m,p,q的值;(2)、有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由、23. “五四”青年节期间,校团委对团员参加活动情况进行表彰,计划分为优秀奖和贡献奖,为此联系印刷公司设计了两种奖状,A,B两家公司都为学校提出了相同规格和单价的两种奖状,其中优秀奖的奖状6元/张,贡献奖的奖状5元/张,经过协商,A公司的优惠条件是:两种奖状都打八折,但要收制版费50元;B公司的优惠条件是:两种奖状都打九折;根据学校要求,优秀奖的个数是贡献奖的2倍还多10个,如果设贡献奖的个数是x个.(1)、分别写出校团委购买A,B两家印刷厂所需要的总费用y1(元)和y2(元)与贡献奖个数x之间的函数关系式;(2)、校团委选择哪家印刷公司比较合算?请说明理由.
(1)、请依据图表中的数据,求出a的值;并直接写出表格中m,p,q的值;(2)、有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由、23. “五四”青年节期间,校团委对团员参加活动情况进行表彰,计划分为优秀奖和贡献奖,为此联系印刷公司设计了两种奖状,A,B两家公司都为学校提出了相同规格和单价的两种奖状,其中优秀奖的奖状6元/张,贡献奖的奖状5元/张,经过协商,A公司的优惠条件是:两种奖状都打八折,但要收制版费50元;B公司的优惠条件是:两种奖状都打九折;根据学校要求,优秀奖的个数是贡献奖的2倍还多10个,如果设贡献奖的个数是x个.(1)、分别写出校团委购买A,B两家印刷厂所需要的总费用y1(元)和y2(元)与贡献奖个数x之间的函数关系式;(2)、校团委选择哪家印刷公司比较合算?请说明理由.四、解答题
-
24. 探索函数y=x+ 的图象和性质:(1)、它的自变量取值范围是;(2)、
当x>0时,我们利用列表法画出函数图象
①填写下表,画出函数的图象:
x
…
1
2
3
4
…
y
…
…

②观察图象,我们发现函数图象有一个最低点,它的坐标是 ,这说明当x= ,函数y有最小值是 ;并且,在该点的左边,y随x的增大而 ,在该点的右边,y随x的增大而 .
③利用上述结论,解决问题:矩形ABCD的面积等于1,当它的长和宽分别为多少时,它的周长最小?
25. 综合:(1)、如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求∠EAF的度数;
 (2)、
(2)、如图②,在Rt△ABD中,∠BAD=90°,AB=AD,点M,N是BD边上的任意两点,且∠MAN=45°,将△ABM绕点A逆时针旋转90°至△ADH位置,连接NH,试判断MN,ND,BM之间的数量关系,并说明理由.
 (3)、在图①中,连接BD分别交AE,AF于点M,N,若DN=3 ,BM=3 ,求MN的长.
(3)、在图①中,连接BD分别交AE,AF于点M,N,若DN=3 ,BM=3 ,求MN的长.