吉林省长春市汽开区2016-2017学年八年级下学期数学期末考试试卷

试卷更新日期：2017-09-13 类型：期末考试

进入出卷网下载

一、选择题

1. 若代数式 $\sqrt{2 x - 4}$ 在实数范围内有意义，则x的取值范围是（）

A、x≥2 B、x＞2 C、x≠2 D、 $x \geq \frac{1}{2}$

查看试题解析
2. 在平面直角坐标系中，将点P（3，6）向下平移8个单位后，得到的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 若双曲线y= $\frac{k}{x}$ 与直线y=2x+1的一个交点的横坐标为﹣1，则k的值为（）

A、﹣1 B、1 C、﹣2 D、2

查看试题解析
4. 如图，在平行四边形ABCD中，∠ABC的平分线交AD于E，∠BED=150°，则∠A的大小为（）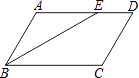

A、150° B、130° C、120° D、100°

查看试题解析
5. 如图，直线l过正方形ABCD的顶点A，BE⊥l于点E，DF⊥l于点F，若BE=2，DF=4，则EF的长为（）

A、2 $\sqrt{2}$ B、2 $\sqrt{5}$ C、6 D、8

查看试题解析
6. 如图，延长矩形ABCD的边BC至点E，使CE=BD，连结AE，如果∠ADB=30°，则∠E的度数是（）

A、45° B、30° C、20° D、15°

查看试题解析
7. 如图，在平面直角坐标系中，菱形OABC的顶点O是原点，顶点B在y轴正半轴上，顶点A在第一象限，菱形的两条对角线长分别是6和4，函数y= $\frac{k}{x}$ （x＜0）的图象经过点C，则k的值为（）

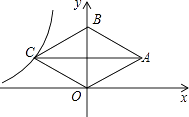A、6 B、﹣6 C、12 D、﹣12

查看试题解析

二、填空题

8. 有一组数据：3，5，5，6，8，这组数据的众数为．

查看试题解析
9. 如果 $\sqrt{x - 3} + \sqrt{y + 2}$ =0，那么xy的值为．

查看试题解析
10. 如果一次函数y=kx+b的图象经过第一、二、四象限，则k的取值范围是， b的取值范围是．

查看试题解析
11. 如图，在四边形ABCD中，AB=BC=CD=DA，对角线AC与BD相交于点O，若不增加任何字母与辅助线，要使四边形ABCD是正方形，则还需增加一个条件是．

查看试题解析
12. 如图，在矩形ABCD中，点E，F分别是AB，CD的中点，连结DE，BF，分别取DE，BF的中点M，N，连结AM，CN，MN，若AB=2 $\sqrt{3}$ ，BC=2 $\sqrt{5}$ ，则图中阴影部分图形的面积和为．

查看试题解析
13. 某通讯公司的4G上网套餐每月上网费用y（单位：元）与上网流量x（单位：兆）的函数关系的图象如图所示．若该公司用户月上网流量超过500兆以后，每兆流量的费用为0.29元，则图中a的值为．

查看试题解析

三、解答题

14. 计算：

(1)、 $\sqrt{27}$ ﹣ $\sqrt{12}$ + $\sqrt{3}$

(2)、 $\frac{\sqrt{12}}{\sqrt{3}}$

(3)、（ $\sqrt{8}$ +5 $\sqrt{6}$ ）× $\sqrt{2}$ ．

查看试题解析
15. 一次函数的图象经过点（4，4）和（2，﹣1），求这个函数的表达式．

查看试题解析
16.
在边长为1个单位长度的小正方形组成的3×3的正方形网格图①、图②中，各画一个顶点在格点上的平行四边形，要求：每个平行四边形均为轴对称图形，每个平行四边形至少有一条边长为 $\sqrt{5}$ ，所画的两个四边形不全等．

查看试题解析
17.
为了让同学们了解自己的体育水平，初二1班的体育刘老师对全班45名学生进行了一次体育模拟测试（得分均为整数），成绩满分为10分，1班的体育委员根据这次测试成绩，制作了统计图和分析表如下：
初二1班体育模拟测试成绩分析表

平均分
方差
中位数
众数
男生

2
8
7
女生
7.92
1.99
8

根据以上信息，解答下列问题：

(1)、这个班共有男生人，共有女生人；

(2)、补全初二1班体育模拟测试成绩分析表；

(3)、你认为在这次体育测试中，1班的男生队、女生队哪个表现更突出一些？并写出一条支持你的看法的理由．

查看试题解析
18. 如图，在平行四边形ABCD中，点E、F分别是AD、BC的中点．求证：AF=CE．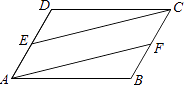

查看试题解析
19. 为了解某小区家庭用电情况，小明随机调查了该小区n户家庭2017年4月的用电量（用电量的数据都是整数），并将所得整数绘制成频数分布直方图如图①所示．

(1)、求n的值，

(2)、小明将所得数据按每户用电量x（度）大小分为三档，①低档：121≤x≤160，②中档：161≤x≤200，③高档：201≤x≤240，并绘制成扇形统计图如图②所示，请帮助他将扇形统计图补充完整．

(3)、该地区对居民用电实行“阶梯收费”，规定：用电量不超过200度按第一阶梯电价收费，超过200度的部分按第二阶梯电价收费，根据以上调查结果，估计2017年4月该小区300户家庭仅按第一阶梯电价收费额户数．

查看试题解析
20. 如图，在△ABC中，AB=AC，AD平分∠BAC交BC于点D，分别过点A，D作AE∥BC，DE∥AB，AE与DE相交于点E，连结CE．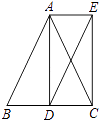

(1)、求证：AE=BD；

(2)、求证：四边形ADCE是矩形．

查看试题解析
21. 甲、乙两个工程队同时开始维修某一段路面，一段时间后，甲队被调往别处，乙队又用了2小时完成了剩余的维修任务．已知乙队每小时维修路面的长度保持不变，甲队每小时维修路面30米．甲、乙两队在此路段维修路面的总长度y（米）与维修时间x（时）之间的函数图象如图所示．

(1)、甲队调离时，甲、乙两队已维修路面的总长度为

(2)、求此次维修路面的总长度a．

(3)、求甲队调离后y与x之间的函数关系式．

查看试题解析
22. 【感知】如图①，四边形ABCD、CEFG均为正方形．可知BE=DG．
【拓展】如图②，四边形ABCD、CEFG均为菱形，且∠A=∠F．求证：BE=DG．
【应用】如图③，四边形ABCD、CEFG均为菱形，点E在边AD上，点G在AD延长线上．若AE=2ED，∠A=∠F，△EBC的面积为8，则菱形CEFG的面积为

查看试题解析
23. 小东根据学习函数的经验，对函数y= $\frac{4}{{(x - 1)}^{2} + 1}$ 的图象与性质进行了探究．下面是小东的探究过程，请补充完整，并解决相关问题：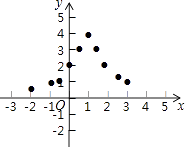

(1)、函数y= $\frac{4}{{(x - 1)}^{2} + 1}$ 的自变量x的取值范围是

(2)、表格是y与x的几组对应值．
x
…
﹣2
﹣1
﹣ $\frac{1}{2}$
0
$\frac{1}{2}$
1
$\frac{3}{2}$
2
$\frac{5}{2}$
3
4
…
y
…
$\frac{2}{5}$
$\frac{4}{5}$
$\frac{16}{13}$
2
$\frac{16}{5}$
4
$\frac{16}{5}$
2
$\frac{16}{13}$
$\frac{4}{3}$
m
…
表中m的值为

(3)、如图，在平面直角坐标系中，描出了以上表中各对对应值为坐标的点．
根据描出的点，画出函数y= $\frac{4}{{(x - 1)}^{2} + 1}$ 的大致图象；

(4)、结合函数图象，请写出函数y= $\frac{4}{{(x - 1)}^{2} + 1}$ 的一条性质：

(5)、如果方程 $\frac{4}{{(x - 1)}^{2} + 1}$ =a有2个解，那么a的取值范围是

查看试题解析

	平均分	方差	中位数	众数
男生		2	8	7
女生	7.92	1.99	8