河南省南阳市南召县2016-2017学年八年级下学期数学期末考试试卷
试卷更新日期:2017-09-13 类型:期末考试
一、选择题
-
1. 化简 的结果为( )A、﹣1 B、1 C、 D、2. 平行四边形、矩形、菱形、正方形都具有的是( )A、对角线互相平分 B、对角线互相垂直 C、对角线相等 D、对角线互相垂直且相等3. PM2.5是指大气中直径小于或等于2.5微米的颗粒物,2.5微米等于0.000 0025米,把0.000 0025用科学记数法表示为( )A、2.5×106 B、0.25×10﹣5 C、25×10﹣7 D、2.5×10﹣64. 已知变量y与x成反比例,当x=3时,y=﹣6,则该反比例函数的解析式为( )A、y= B、y=﹣ C、y= D、y=﹣5. 如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲
乙
丙
丁
平均数(cm)
185
180
185
180
方差
3.6
3.6
7.4
8.1
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A、甲 B、乙 C、丙 D、丁6. 如图,矩形ABCD沿AE折叠,使D点落在BC边上点F处,如果∠BAF=60°,则∠EAF等于( )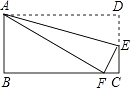 A、15° B、30° C、45° D、60°7. 如图,菱形ABCD的周长是20,对角线AC,BD相交于点O,若BD=6,则菱形ABCD的面积是( )
A、15° B、30° C、45° D、60°7. 如图,菱形ABCD的周长是20,对角线AC,BD相交于点O,若BD=6,则菱形ABCD的面积是( )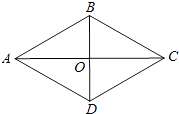 A、6 B、12 C、24 D、488. 如图是交警在一个路口统计的某个时段来往车辆的车速(单位:千米/时)情况.则这些车的车速的众数、中位数分别是( )
A、6 B、12 C、24 D、488. 如图是交警在一个路口统计的某个时段来往车辆的车速(单位:千米/时)情况.则这些车的车速的众数、中位数分别是( ) A、8,6 B、8,5 C、52,53 D、52,529. 如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A、8,6 B、8,5 C、52,53 D、52,529. 如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )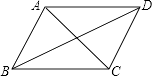 A、当AB=BC时,四边形ABCD是菱形 B、当AC⊥BD时,四边形ABCD是菱形 C、当∠ABC=90°时,四边形ABCD是矩形 D、当AC=BD时,四边形ABCD是正方形10.
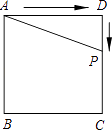
A、当AB=BC时,四边形ABCD是菱形 B、当AC⊥BD时,四边形ABCD是菱形 C、当∠ABC=90°时,四边形ABCD是矩形 D、当AC=BD时,四边形ABCD是正方形10.如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→D→C→B→A,设P点经过的路程为x,以点A、P、D为顶点的三角形的面积是y,则下列图象能大致反映y与x的函数关系的是( )
 A、
A、 B、
B、 C、
C、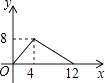 D、
D、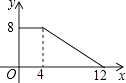
二、填空题
-
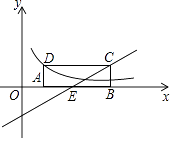
11. (﹣ )﹣1+(1﹣ )0= .12. 学校制定成绩的评价方案:期中成绩占30%,期末成绩占70%,小李期中与期末成绩分别为80分和90分,则本学期他的成绩为分.13. 分式方程 = 的解为 .14. 如图,在平面直角坐标系中,有一矩形ABCD,边AB在x轴的正半轴上,AB=3,BC=1,直线y= ﹣1经过点C交x轴于点E,若反比例函数y= 的图象经过点D,则k的值为 .
 15. 如图,在矩形ABCD中,AD=5,AB=8,点E为DC边上的一个动点,把△ADE沿AE折叠,当点D的对应点刚好D落在矩形ABCD的对称轴上时,则DE的长为 .
15. 如图,在矩形ABCD中,AD=5,AB=8,点E为DC边上的一个动点,把△ADE沿AE折叠,当点D的对应点刚好D落在矩形ABCD的对称轴上时,则DE的长为 .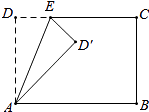
三、解答题
-
16. 先化简,再求值:(1﹣ )÷ (从﹣1、2、3中选择一个适当的数作为x值代入).17. 学校举行了主题为“让历史照亮未来”的演讲比赛,其中代表七、八年级参赛的两队各10人的比赛成绩如下表(10分制):
七年级队
7
8
9
7
10
10
9
10
10
10
八年级队
10
8
7
9
8
10
10
9
10
9
(1)、请直接写出七年级队成绩的中位数为 , 八年级队成绩的众数为;(2)、若七、八年级队的平均成绩均为9分,请分别计算七、八年级队的方差.18. 如图,矩形ABCD中,对角线AC的垂直平分线交AD、BC于点E、F,AC与EF交于点O,连结AF、CE. (1)、求证:四边形AFCE是菱形;(2)、若AB=3,AD=4,求菱形AFCE的边长.19. 随着互联网进入成熟发展阶段,手机已成为我们生活中必不可少的信息交流工具,某商场计划购进A、B两种不同品牌的手机共50部,A、B两种品牌的手机的进价和售价如表所示:
(1)、求证:四边形AFCE是菱形;(2)、若AB=3,AD=4,求菱形AFCE的边长.19. 随着互联网进入成熟发展阶段,手机已成为我们生活中必不可少的信息交流工具,某商场计划购进A、B两种不同品牌的手机共50部,A、B两种品牌的手机的进价和售价如表所示:品牌
价格
A品牌
B品牌
进价(元/部)
3800
3000
售价(元/部)
4500
3500
设该商场计划购进A品牌手机x台,两种品牌的手机全部销售完后可获得利润为y元.
(1)、求y与x之间的函数关系式;(2)、若商场购进B品牌手机的数量为20部,两种品牌的手机全部销售完后可获利多少?20. 如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2)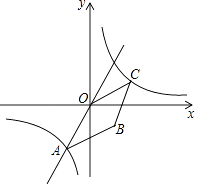 (1)、求反比例函数的解析式;(2)、若双曲线上一点C(2,n)沿OA方向平移 个单位长度到达点B(如图),连接AB、OC,则线段AB与OC的关系是 .21. 小明根据华师版八年级下册教材P37学习内容,对函数y= x2的图象和性质进行了探究,试将如下尚不完整的过程补充完整.
(1)、求反比例函数的解析式;(2)、若双曲线上一点C(2,n)沿OA方向平移 个单位长度到达点B(如图),连接AB、OC,则线段AB与OC的关系是 .21. 小明根据华师版八年级下册教材P37学习内容,对函数y= x2的图象和性质进行了探究,试将如下尚不完整的过程补充完整.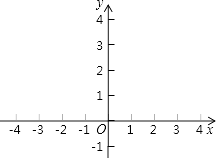 (1)、自变量x的取值范围是全体实数,x与y的几组对应数值如表:
(1)、自变量x的取值范围是全体实数,x与y的几组对应数值如表:x
…
﹣4
n
﹣2
﹣1
0
1
2
3
4
…
y
…
8
4.5
2
0.5
0
0.5
2
4.5
8
…
其中n=;
(2)、如图,在平面直角三角形坐标系xOy中,已描出了以上表中的部分数值为坐标的点,根据描出的点,画出该函数的大致图象.(3)、根据画出的函数图象,小明观察发现:该函数有最小值,没有最大值;当函数值取最小时,自变量x的值为 .(4)、进一步探究函数的图象发现:①若点A(xa , ya),点B(xb , yb)在函数y= 的图象上;
当xa<xb<0时,ya与yb的大小关系是;
当0<xa<xb时,ya与yb的大小关系是;
②直线y1恰好经过函数的图象上的点(﹣2,2)与(1,0.5);当y<y1时,x的取值范围是 .
22. 在平行四边形ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连接EG、GF、FH、HE.(1)、如图1,试判断四边形EGFH的形状,并说明理由;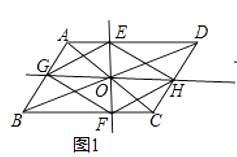 (2)、如图2,当EF⊥GH,AC=BD时,四边形EGFH的形状是;
(2)、如图2,当EF⊥GH,AC=BD时,四边形EGFH的形状是;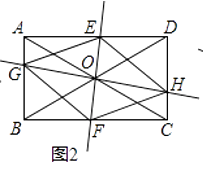 (3)、在(2)的条件下,若AC⊥BD(如图3),四边形EGFH的形状是 .
(3)、在(2)的条件下,若AC⊥BD(如图3),四边形EGFH的形状是 .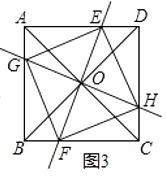 23.
23.如图,已知函数y=﹣ x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2.
 (1)、求点A的坐标;(2)、在x轴上有一动点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=﹣ +b和y=x的图象于点C、D.
(1)、求点A的坐标;(2)、在x轴上有一动点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=﹣ +b和y=x的图象于点C、D.①若OB=2CD,求a的值;
②是否存在这样的点P,使以B、O、C、D为顶点的四边形是平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.