2015年广东省广州市中考数学试卷
试卷更新日期：2016-04-22 类型：中考真卷
一、单选题
-
1. 已知2是关于x的方程x2﹣2mx+3m=0的一个根， 并且这个方程的两个根恰好是等腰三角形ABC的两条边长， 则三角形ABC的周长为（ ）
A、10 B、14 C、10或14 D、8或102. 已知圆的半径是2 ， 则该圆的内接正六边形的面积是（ ）A、3 B、9 C、18 D、363. 下列命题中，真命题的个数有（ ）①对角线互相平分的四边形是平行四边形；②两组对角分别相等的四边形是平行四边形；③一组对边平行，另一组对边相等的四边形是平行四边形．
A、3个 B、2个 C、1个 D、0个4. 已知a，b满足方程组 ， 则a+b的值为（ ）
A、-4 B、4 C、-2 D、25.如图是一个几何体的三视图，则该几何体的展开图可以是（ ）
A、
B、
C、
D、
6. 下列计算正确的是（ ）A、ab•ab=2ab B、（2a）3=2a3 C、3﹣=3（a≥0） D、•=（a≥0，b≥0）7. 两名同学进行了10次三级蛙跳测试，经计算，他们的平均成绩相同，若要比较这两名同学的成绩哪一位更稳定，通常还需要比较他们成绩的（ ）A、众数 B、中位数 C、方差 D、以上都不对8. 已知⊙O的半径为5，直线l是⊙O的切线，则点O到直线l的距离是（ ）A、2.5 B、3 C、5 D、109.将图中所示的图案以圆心为中心，旋转180°后得到的图案是（ ）
A、
B、
C、
D、
10. 四个数﹣3.14，0，1，2中为负数的是（ ）A、﹣3.14 B、0 C、1 D、2二、填空题
-
11.
如图，四边形ABCD中，∠A=90°，AB=3 ， AD=3，点M，N分别为线段BC，AB上的动点（含端点，但点M不与点B重合），点E，F分别为DM，MN的中点，则EF长度的最大值为 ．
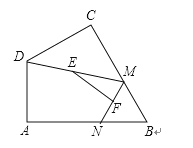12.如图，△ABC中，DE是BC的垂直平分线，DE交AC于点E，连接BE．若BE=9，BC=12，则cosC= ．
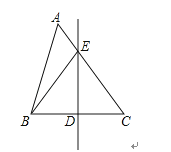13. 某水库的水位在5小时内持续上涨，初始水位高度为6米，水位以每小时0.3米的速度匀速上升，则水库的水位高度y（米）与时间x（小时）（0≤x≤5）的函数关系式为 ．
14. 分解因式：2mx﹣6my= ．15.根据环保局公布的广州市2013年至2014年PM2.5的主要来源的数据，制成扇形统计图，其中所占百分比最大的主要来源是 （填主要来源的名称）.
16.如图，AB∥CD，直线l分别与AB，CD相交，若∠1=50°，则∠2的度数为 ．
三、计算题
-
17. 解方程：5x=3（x﹣4）
四、解答题
-
18.
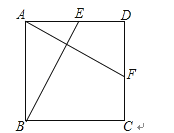
如图，正方形ABCD中，点E，F分别在AD，CD上，且AE=DF，连接BE，AF．求证：BE=AF．
五、综合题
-
19.
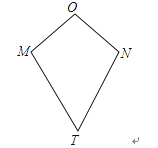
如图，四边形OMTN中，OM=ON，TM=TN，我们把这种两组邻边分别相等的四边形叫做筝形．
(1)、试探究筝形对角线之间的位置关系，并证明你的结论；
(2)、在筝形ABCD中，已知AB=AD=5，BC=CD，BC＞AB，BD、AC为对角线，BD=8，①是否存在一个圆使得A，B，C，D四个点都在这个圆上？若存在，求出圆的半径；若不存在，请说明理由；
②过点B作BF⊥CD，垂足为F，BF交AC于点E，连接DE，当四边形ABED为菱形时，求点F到AB的距离．
20. 已知O为坐标原点，抛物线y1=ax2+bx+c（a≠0）与x轴相交于点A（x1 ， 0），B（x2 ， 0），与y轴交于点C，且O，C两点间的距离为3，x1•x2＜0，|x1|+|x2|=4，点A，C在直线y2=﹣3x+t上．(1)、求点C的坐标(2)、当y1随着x的增大而增大时，求自变量x的取值范围；(3)、将抛物线y1向左平移n（n＞0）个单位，记平移后y随着x的增大而增大的部分为P，直线y2向下平移n个单位，当平移后的直线与P有公共点时，求2n2﹣5n的最小值．21.2015•广州）如图，AC是⊙O的直径，点B在⊙O上，∠ACB=30°
(1)、利用尺规作∠ABC的平分线BD，交AC于点E，交⊙O于点D，连接CD（保留作图痕迹，不写作法）(2)、在（1）所作的图形中，求△ABE与△CDE的面积之比．22. 4件同型号的产品中，有1件不合格品和3件合格品．(1)、从这4件产品中随机抽取1件进行检测，求抽到的是不合格品的概率；(2)、从这4件产品中随机抽取2件进行检测，求抽到的都是合格品的概率；(3)、在这4件产品中加入x件合格品后，进行如下试验：随机抽取1件进行检测，然后放回，多次重复这个试验，通过大量重复试验后发现，抽到合格品的频率稳定在0.95，则可以推算出x的值大约是多少？23. 某地区2013年投入教育经费2500万元，2015年投入教育经费3025万元．(1)、求2013年至2015年该地区投入教育经费的年平均增长率(2)、根据（1）所得的年平均增长率，预计2016年该地区将投入教育经费多少万元
-
-
