陕西省榆林市2020届高三下学期理数3月线上高考模拟测试试卷

试卷更新日期：2020-04-27 类型：高考模拟

进入出卷网下载

一、单选题

1. 设集合 $A = {x | - 2 < x ⩽ 2 ， x \in Z} ， B = {x | \log_{2} x < 1}$ ，则 $A \cap B =$ （）

A、 $(0 ， 2)$ B、 $(- 2 ， 2]$ C、 ${1}$ D、 ${- 1 ， 0 ， 1 ， 2}$

查看试题解析
2. 在复平面内，复数 $z = a + b i$ （ $a$ ， $b \in R$ ）对应向量 $\vec{O Z}$ （O为坐标原点），设 $| \vec{O Z} | = r$ ，以射线Ox为始边，OZ为终边旋转的角为 $θ$ ，则 $z = r (\cos θ + i \sin θ)$ ，法国数学家棣莫弗发现了棣莫弗定理： $z_{1} = r_{1} (\cos θ_{1} + i \sin θ_{1})$ ， $z_{2} = r_{2} (\cos θ_{2} + i \sin θ_{2})$ ，则 $z_{1} z_{2} = r_{1} r_{2} [\cos (θ_{1} + θ_{2}) + i \sin (θ_{1} + θ_{2})]$ ，由棣莫弗定理可以导出复数乘方公式： ${[r (\cos θ + i \sin θ)]}^{n} = r^{n} (\cos n θ + i \sin n θ)$ ，已知 $z = {(\sqrt{3} + i)}^{4}$ ，则 $| \bar{z} | =$ （）

A、 $2 \sqrt{3}$ B、4 C、 $8 \sqrt{3}$ D、16

查看试题解析
3. 为比较甲、乙两名高中学生的数学素养，对课程标准中规定的数学六大素养进行指标测验（指标值满分为100分，分值高者为优），根据测验情况绘制了如图所示的六大素养指标雷达图，则下面叙述不正确的是（）

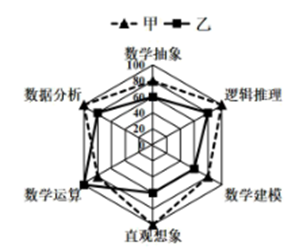A、甲的数据分析素养优于乙 B、乙的数据分析素养优于数学建模素养 C、甲的六大素养整体水平优于乙 D、甲的六大素养中数学运算最强

查看试题解析
4. 已知 $\sin α - 2 \cos α = 1 ， α \in (π ， \frac{3 π}{2})$ ，则 $\frac{1 - \tan \frac{α}{2}}{1 + \tan \frac{α}{2}} =$ （）

A、 $- \frac{1}{2}$ B、 $- 2$ C、 $\frac{1}{2}$ D、2

查看试题解析
5. 在 $Δ A B C$ 中，点D是线段BC上任意一点， $2 \vec{A M} = \vec{A D}$ ， $\vec{B M} = λ \vec{A B} + μ \vec{A C}$ ，则 $λ + μ =$ （）

A、 $- \frac{1}{2}$ B、-2 C、 $\frac{1}{2}$ D、2

查看试题解析
6. 设椭圆 $E$ ： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的右顶点为A ，右焦点为F ， B、C为椭圆上关于原点对称的两点，直线BF交直线AC于M ，且M为AC的中点，则椭圆E的离心率是（）

A、 $\frac{2}{3}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

查看试题解析
7. 《九章算术》“少广”算法中有这样一个数的序列：列出“全步”（整数部分）及诸分子分母，以最下面的分母遍乘各分子和“全步”，各自以分母去约其分子，将所得能通分之分数进行通分约简，又用最下面的分母去遍乘诸（未通者）分子和以通之数，逐个照此同样方法，直至全部为整数，例如： $n = 2$ 及 $n = 3$ 时，如图：

记 $S_{n}$ 为每个序列中最后一列数之和，则 $S_{6}$ 为（）

A、147 B、294 C、882 D、1764

查看试题解析
8. 已知函数 $f (x) = \frac{x^{3} + \sin x}{(1 + x) (m - x) + e^{x} + e^{- x}}$ 为奇函数，则 $m =$ （）

A、 $\frac{1}{2}$ B、1 C、2 D、3

查看试题解析
9. 已知正四面体的内切球体积为v ，外接球的体积为V ，则 $\frac{V}{v} =$ （）

A、4 B、8 C、9 D、27

查看试题解析
10. 要得到函数 $f^{'} (x) = \sin (3 x + \frac{π}{3})$ 的导函数 $f^{'} (x)$ 的图像，只需将 $f (x)$ 的图像（）

A、向右平移 $\frac{π}{3}$ 个单位长度，再把各点的纵坐标伸长到原来的3倍 B、向右平移 $\frac{π}{6}$ 个单位长度，再把各点的纵坐标缩短到原来的 $\frac{1}{3}$ 倍 C、向左平移 $\frac{π}{3}$ 个单位长度，再把各点的纵坐标缩短到原来的 $\frac{1}{3}$ 倍 D、向左平移 $\frac{π}{6}$ 个单位长度，再把各点的纵坐标伸长到原来的3倍

查看试题解析
11. 已知平面 $A B C D ⊥$ 平面 $A D E F ， A B ⊥ A D ， C D ⊥ A D$ ，且 $A B = 3 ， A D = C D = 6 ， A D E F$ 是正方形，在正方形 $A D E F$ 内部有一点 $M$ ，满足 $M B ， M C$ 与平面 $A D E F$ 所成的角相等，则点 $M$ 的轨迹长度为（）

A、 $\frac{4}{3}$ B、16 C、 $\frac{4}{3} π$ D、 $8 π$

查看试题解析
12. 已知 $y = a x + b$ 与函数 $f (x) = 2 \ln x + 5$ 和 $g (x) = x^{2} + 4$ 都相切，则不等式组 ${\begin{array}{l} x - a y + 3 \geq 0 \\ x + b y - 2 \geq 0 \end{array}$ 所确定的平面区域在 $x^{2} + y^{2} + 2 x - 2 y - 22 = 0$ 内的面积为（）

A、 $2 π$ B、 $3 π$ C、 $6 π$ D、 $12 π$

查看试题解析

二、填空题

13. 设

x_{1} 、 x_{2} 、 x_{3} 、 x_{4}

为互不相等的正实数，随机变量

X

和

Y

的分布列如下表，若记

D X

，

D Y

分别为

X ， Y

的方差，则

D X

D Y

．（填>，<，=）

$X$	$x_{1}$	$x_{2}$	$x_{3}$	$x_{4}$
$Y$	$\frac{x_{1} + x_{2}}{2}$	$\frac{x_{2} + x_{3}}{2}$	$\frac{x_{3} + x_{4}}{2}$	$\frac{x_{4} + x_{1}}{2}$
$P$	$\frac{1}{4}$	$\frac{1}{4}$	$\frac{1}{4}$	$\frac{1}{4}$

查看试题解析

14. $Δ A B C$ 的三个内角A ， B ， C所对应的边分别为a ， b ， c ，已知 $2 b \cos A = 2 c + \sqrt{3} a$ ，则 $∠ B =$ .

查看试题解析
15. 若双曲线C： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ （ $a > 0$ ， $b > 0$ ）的顶点到渐近线的距离为 $\frac{b}{2}$ ，则 $\frac{b^{2} + 1}{\sqrt{3} a}$ 的最小值.

查看试题解析
16. 若奇函数 $f (x)$ 满足 $f (x + 2) = - f (x)$ ， $g (x)$ 为R上的单调函数，对任意实数 $x \in R$ 都有 $g [g (x) - 2^{x} + 2] = 1$ ，当 $x \in [0 ， 1]$ 时， $f (x) = g (x)$ ，则 $f (\log_{2} 12) =$ .

查看试题解析

三、解答题

17. 已知数列 ${a_{n}}$ 为公差为d的等差数列， $d > 0$ ， $a_{4} = 4$ ，且 $a_{1}$ ， $a_{3}$ ， $a_{9}$ 依次成等比数列， $b_{n} = 2^{a_{n}}$ .

(1)、求数列 ${b_{n}}$ 的前n项和 $S_{n}$ ；

(2)、若 $c_{n} = \frac{2 b_{n}}{S_{n} \cdot S_{n + 1}}$ ，求数列 ${c_{n}}$ 的前n项和为 $T_{n}$ .

查看试题解析
18. 在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 是平行四边形， $P D ⊥$ 底面 $A B C D ， P D = A D = 1 ， A B = \sqrt{5} ， \sin ∠ A B D = \frac{\sqrt{5}}{5}$ ．

(1)、证明： $P A ⊥ B D$ ；

(2)、求二面角 $A - P B - C$ 的正弦值．

查看试题解析
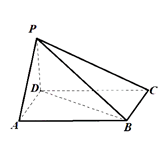19. 已知动圆过定点 $F (0 ， 1)$ ，且与直线 $l ： y = - 1$ 相切，动圆圆心的轨迹为 $C$ ，过 $F$ 作斜率为 $k (k \neq 0)$ 的直线 $m$ 与 $C$ 交于两点 $A ， B$ ，过 $A ， B$ 分别作 $C$ 的切线，两切线的交点为 $P$ ，直线 $P F$ 与 $C$ 交于两点 $M ， N$ ．

(1)、证明：点 $P$ 始终在直线 $l$ 上且 $P F ⊥ A B$ ；

(2)、求四边形 $A M B N$ 的面积的最小值．

查看试题解析

20. 2019年12月以来，湖北省武汉市持续开展流感及相关疾病监测，发现多起病毒性肺炎病例，均诊断为病毒性肺炎/肺部感染，后被命名为新型冠状病毒肺炎（CoronaVirusDisease2019，COVID—19），简称“新冠肺炎”.下图是2020年1月15日至1月24日累计确诊人数随时间变化的散点图.

为了预测在未釆取强力措施下，后期的累计确诊人数，建立了累计确诊人数y与时间变量t的两个回归模型，根据1月15日至1月24日的数据（时间变量t的值依次1，2，…，10）建立模型 $\hat{y} = c + d t$ 和 $\hat{y} = a + b \cdot {1.5}^{t}$ .

附：对于一组数据（ $(u_{1} ， v_{1})$ ， $(u_{2} ， v_{2})$ ，……， $(u_{n} ， v_{n})$ ，其回归直线 $v = a + β u$ 的斜率和截距的最小二乘估计分别为 $\hat{β} = \frac{\sum_{i = 1}^{n} (u_{i} - \bar{u}) (v_{i} - \bar{v})}{\sum_{i = 1}^{n} {(u_{i} - \bar{u})}^{2}}$ ， $\hat{α} = \bar{v} - \hat{β} \bar{u}$ .

参考数据：其中 $ω_{i} = {1.5}^{t_{i}}$ ， $\bar{ω} = \frac{1}{10} \sum_{i = 1}^{10} ω_{i}$ .

$\bar{t}$	$\bar{y}$	$\bar{ω}$	$\sum_{i = 1}^{10} t_{i}^{2}$	$\sum_{i = 1}^{10} ω_{i}^{2}$	$\sum_{i = 1}^{10} t_{i} y_{i}$	$\sum_{i = 1}^{10} ω_{i} y_{i}$	${1.5}^{11}$	${1.5}^{12}$	${1.5}^{13}$	${1.5}^{14}$	${1.5}^{15}$
5.5	390	19	385	7640	31525	154700	100	150	225	338	507

(1)、根据散点图判断，

\hat{y} = c + d t

与

\hat{y} = a + b \cdot {1.5}^{t}

哪一个适宜作为累计确诊人数y与时间变量t的回归方程类型？（给出判断即可，不必说明理由）

(2)、以下是1月25日至1月29日累计确诊人数的真实数据，根据（2）的结果回答下列问题：

时间	1月25日	1月26日	1月27日	1月28日	1月29日
累计确诊人数的真实数据	1975	2744	4515	5974	7111

（ⅰ）当1月25日至1月27日这3天的误差（模型预测数据与真实数据差值的绝对值与真实数据的比值）都小于0.1则认为模型可靠，请判断（2）的回归方程是否可靠？

（ⅱ）2020年1月24日在人民政府的强力领导下，全国人民共同采取了强力的预防“新冠肺炎”的措施，若采取措施5天后，真实数据明显低于预测数据，则认为防护措施有效，请判断预防措施是否有效？

查看试题解析

21. 已知函数 $f (x) = \ln x - a x + a$ ，其中 $a > 0$ ．

(1)、讨论函数 $f (x)$ 的零点个数；

(2)、求证： $e^{x} + \sin x > x \ln x + 1$ ．

查看试题解析
22. 在直角坐标系xOy中，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，已知 $C_{1}$ ： $x^{2} + y^{2} - 2 y = 0$ ， $C_{2}$ ： $\sqrt{3} x + y = 6$ ， $C_{3}$ ： $k x - y = 0 (k > 0)$ .

(1)、求 $C_{1}$ 与 $C_{2}$ 的极坐标方程

(2)、若 $C_{1}$ 与 $C_{3}$ 交于点A ， $C_{2}$ 与 $C_{3}$ 交于点B ， $| O A | = λ | O B |$ ，求 $λ$ 的最大值.

查看试题解析
23. 已知函数 $f (x) = 2 | x | + | x - 4 |$ ，设 $f (x)$ 的最小值为m.

(1)、求m的值；

(2)、是否存在实数a ， b ，使得 $a + 2 b = 2$ ， $\frac{1}{a} + \frac{2}{b} = m$ ？并说明理由.

查看试题解析