广西玉林市陆川县2016-2017学年八年级下学期数学期末考试试卷
试卷更新日期:2017-09-13 类型:期末考试
一、选择题
-
1. 下列根式中不是最简二次根式的是( )A、 B、 C、 D、2. 顺次连接四边形ABCD的各边中点所得的四边形是( )A、矩形 B、菱形 C、平行四边形 D、正方形3. 在下列各图象中,y不是x函数的是( )A、
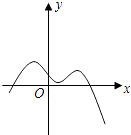 B、
B、 C、
C、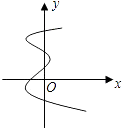 D、
D、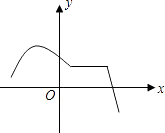 4. 下列给出的条件中,不能判断四边形ABCD是平行四边形的是( )A、AB∥CD,AD=BC B、∠A=∠C,∠B=∠D C、AB∥CD,AD∥BC D、AB=CD,AD=BC5. 下列计算中:① =2 ;② =4 ;③ ﹣ = ;④ =﹣2;⑤ = ﹣ =1,其中正确的有( )A、1个 B、2个 C、3个 D、4个6. 商厦信誉楼女鞋专柜试销一种新款女鞋,一个月内销售情况如表所示:
4. 下列给出的条件中,不能判断四边形ABCD是平行四边形的是( )A、AB∥CD,AD=BC B、∠A=∠C,∠B=∠D C、AB∥CD,AD∥BC D、AB=CD,AD=BC5. 下列计算中:① =2 ;② =4 ;③ ﹣ = ;④ =﹣2;⑤ = ﹣ =1,其中正确的有( )A、1个 B、2个 C、3个 D、4个6. 商厦信誉楼女鞋专柜试销一种新款女鞋,一个月内销售情况如表所示:型号
22
22.5
23
23.5
24
24.5
25
数量(双)
2
6
11
15
7
3
4
经理最关心的是,哪种型号的鞋销量最大.对他来说,下列统计量中最重要的是( )
A、平均数 B、众数 C、中位数 D、方差7. 假设汽车匀速行驶在高速公路上,那么在下列各量中,变量的个数是( )①行驶速度;②行驶时间;③行驶路程;④汽车油箱中的剩余油量.
A、1个 B、2个 C、3个 D、4个8. 学校组织才艺表演比赛,前6名获奖.有13位同学参加比赛且他们所得的分数互不相同.某同学知道自己的比赛分数后,要判断自己能否获奖,在这13名同学成绩的统计量中只需知道一个量,它是( )A、众数 B、方差 C、中位数 D、平均数9. 甲、乙、丙、丁四位同学五次数学测验成绩统计如表.如果从这四位同学中,选出一位成绩较好且状态稳定的同学参加全国数学联赛,那么应选( )甲
乙
丙
丁
平均数
80
85
85
80
方 差
42
42
54
59
A、甲 B、乙 C、丙 D、丁10. 如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD= ,则BC的长为( ) A、 ﹣1 B、 +1 C、 ﹣1 D、 +111. 两条直线y=ax+b与y=bx+a在同一直角坐标系中的图象位置可能是( )
A、 ﹣1 B、 +1 C、 ﹣1 D、 +111. 两条直线y=ax+b与y=bx+a在同一直角坐标系中的图象位置可能是( )
A、 B、
B、 C、
C、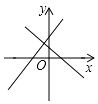 D、
D、 12. 如图,在矩形ABCD中,AB=2,AD=3,点E是BC边上靠近点B的三等分点,动点P从点A出发,沿路径A→D→C→E运动,则△APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是( )
12. 如图,在矩形ABCD中,AB=2,AD=3,点E是BC边上靠近点B的三等分点,动点P从点A出发,沿路径A→D→C→E运动,则△APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
13. 一条直线与已知直线y=﹣3x+1平行,这条直线可以为 .14. 数据﹣4,﹣2,0,2,4的方差是 .15. 计算:( ﹣2)2016×( +2)2017= .16. 如图,一次函数y1=k1+b1与y2=k2+b2的图象相交于A(3,2),则不等式(k2﹣k1)x+b2﹣b1>0的解集为 .
 17. 如图,P是矩形ABCD的边AD上一个动点,矩形的两条边AB、BC的长分别为6和8,那么点P到矩形的两条对角线AC和BD的距离之和是 .
17. 如图,P是矩形ABCD的边AD上一个动点,矩形的两条边AB、BC的长分别为6和8,那么点P到矩形的两条对角线AC和BD的距离之和是 . 18.
18.如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x﹣6上时,线段BC扫过的面积为 cm2 .

三、解答题
-
19. |2 ﹣3|﹣(﹣ )﹣2+ +( ﹣ )0 .20. 已知y与x﹣2成正比例,当x=3时,y=2.(1)、求y与x之间的函数关系式;(2)、证明:△ABC是直角三角形.(3)、当﹣2<x<3时,求y的范围.(4)、请求图中阴影部分的面积.21. 如图,已知正方形ABCD,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB.
 (1)、求证:四边形PMAN是正方形;(2)、求证:EM=BN.22. 如图,平面直角坐标系中,一次函数y=﹣2x+1的图象与y轴交于点A.
(1)、求证:四边形PMAN是正方形;(2)、求证:EM=BN.22. 如图,平面直角坐标系中,一次函数y=﹣2x+1的图象与y轴交于点A. (1)、若点A关于x轴的对称点B在一次函数y= x+b的图象上,求b的值,并在同一坐标系中画出该一次函数的图象;(2)、求这两个一次函数的图象与y轴围成的三角形的面积.23. 为了倡导“节约用水,从我做起”,黄冈市政府决定对市直机关500户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中100户家庭一年的月平均用水量(单位:吨).并将调查结果制成了如图所示的条形统计图.
(1)、若点A关于x轴的对称点B在一次函数y= x+b的图象上,求b的值,并在同一坐标系中画出该一次函数的图象;(2)、求这两个一次函数的图象与y轴围成的三角形的面积.23. 为了倡导“节约用水,从我做起”,黄冈市政府决定对市直机关500户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中100户家庭一年的月平均用水量(单位:吨).并将调查结果制成了如图所示的条形统计图. (1)、请将条形统计图补充完整;(2)、求这100个样本数据的平均数,众数和中位数;(3)、根据样本数据,估计黄冈市直机关500户家庭中月平均用水量不超过12吨的约有多少户?24. 某土特产公司组织20辆汽车装运甲、乙、丙三种土特产共120吨去外地销售.按计划20辆车都要装运,每辆汽车只能装运同一种土特产,且必须装满,根据下表提供的信息,解答以下问题:
(1)、请将条形统计图补充完整;(2)、求这100个样本数据的平均数,众数和中位数;(3)、根据样本数据,估计黄冈市直机关500户家庭中月平均用水量不超过12吨的约有多少户?24. 某土特产公司组织20辆汽车装运甲、乙、丙三种土特产共120吨去外地销售.按计划20辆车都要装运,每辆汽车只能装运同一种土特产,且必须装满,根据下表提供的信息,解答以下问题:土特产品种
甲
乙
丙
每辆汽车运载量(吨)
8
6
5
每吨土特产获利(百元)
12
16
10
(1)、设装运甲种土特产的车辆数为x,装运乙种土特产的车辆数为y,求y与x之间的函数关系式.(2)、如果装运每种土特产的车辆都不少于3辆,那么车辆的安排方案有几种并写出每种安排方案.(3)、若要使此次销售获利最大,应采用(2)中哪种安排方案?并求出最大利润的值.25. 如图,在平面直角坐标系中,已知直线y=kx+6与x轴、y轴分别交于A、B两点,且△ABO的面积为12. (1)、求k的值;(2)、若点P为直线AB的一动点,P点运动到什么位置时,△PAO使以OA为底的等腰三角形?求出此时点P的坐标;(3)、在(2)的条件下,坐标平面内是否存在点M,使以P、B、O、M为顶点组成的平行四边形为菱形?若存在,求出点M坐标;若不存在,试说明理由.
(1)、求k的值;(2)、若点P为直线AB的一动点,P点运动到什么位置时,△PAO使以OA为底的等腰三角形?求出此时点P的坐标;(3)、在(2)的条件下,坐标平面内是否存在点M,使以P、B、O、M为顶点组成的平行四边形为菱形?若存在,求出点M坐标;若不存在,试说明理由.