备考2020年中考数学二轮复习拔高训练卷 专题9 锐角三角函数
试卷更新日期：2020-04-27 类型：二轮复习
一、单选题
-
1. 如图，在△ABC中，∠A＝90°，AB＝3，BC＝5，则cosB等于（ ）
A、 B、 C、 D、2. 如图，在四边形ABCD中，E，F分别是AB，AD中点，若EF=6，BC=13，CD=5，则tanC=（ ）
A、 B、 C、 D、3. 如图，在Rt△ABC中，∠C=90°，BC=a，则AB的长是（ ）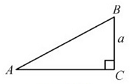
A、 B、 C、asinA D、acosA4. 在直角三角形中各边都扩大2倍，则锐角A的正弦值与余弦值都（ ）A、缩小2倍 B、扩大2倍 C、不变 D、不能确定5. 若∠A是锐角，且sinA= ，则（ ）A、0°<∠A<30° B、30°<∠A<45° C、45°<∠A<60° D、60°<∠A<90°6. 在Rt△ABC中，∠C=90°，CD是高，如果AD=m，∠A=α，那么BC的长为（ ）A、m·tanα·cosα B、m·cotα·cosα C、 D、7. 在Rt△ABC中，∠C=90° ， 则下列式子成立的是（ ）A、sinA=sinB B、sinA=cosB C、tanA=tanB D、cosA=tanB8. 点（-sin60°，cos60°）关于y轴对称的点的坐标是（ ）A、（ ， ） B、（- ， ） C、（- ，- ） D、（- ，- ）9. 如图，一块矩形木板ABCD斜靠在墙边（OC⊥OB，点A，B，C，D，O在同一平面内） 。已知AB=a，AD=b，∠BCO=θ，则点A到OC的距离等于（ ）
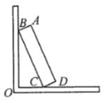A、asinθ+bsinθ B、acosθ+bcosθ C、asinθ+bcosθ D、acosθ+bsinθ10. 如图，在坡度为 的山坡上种树，要求相邻两棵树的水平距离是6m，则斜坡上相邻两棵树的坡面距离是（ ）
A、3m B、3 m C、12m D、6m11. 一艘轮船从港口O出发，以15海里/时的速度沿北偏东60°的方向航行4小时后到达A处，此时观测到其正西方向50海里处有一座小岛B．若以港口O为坐标原点，正东方向为x轴的正方向，正北方向为y轴的正方向，1海里为1个单位长度建立平面直角坐标系（如图），则小岛B所在位置的坐标是（ ）
A、（30 -50，30） B、（30，30 -50） C、（30 ，30） D、（30，30 ）12. 如图，AB是圆锥的母线，BC为底面直径，已知BC＝6 cm，圆锥的侧面积为15π cm2 ， 则sin∠ABC的值为（ ）
A、 B、 C、 D、二、填空题
-
13. 若tan（α–15°）= ，则锐角α的度数是 ．14. 如图，将一张矩形纸片ABCD沿CE折叠，B点恰好落在AD边上，设此点为F，若AB：BC＝4：5，则tan∠CFD＝.
15. 如图，O是坐标原点，边长为2的菱形OABC的顶点C在x轴的负半轴上，cos∠AOC＝ ，函数 的图象经过顶点B，则k的值为.
16. 一个长方体木箱沿斜面下滑，当木箱滑至如图位置时，AB=3m，已知木箱高BE= m，斜面坡脚为30°，则木箱顶端E距离地面AC的高度EF为m。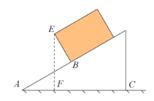
17. 无人机于空中A处测得某建筑顶部B处的仰角为45°，测得该建筑底部C处的俯角为17°．若无人机的飞行高度AD为62m，则该建筑的高度BC为m．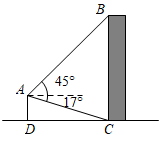
（参考数据：sin17°≈0.29，cos17°≈0.96，tan17°≈0.31）
18. 如图，小明为了测量小河对岸大树BC的高度，他在点A测得大树顶端B的仰角是 ，沿斜坡走 米到达斜坡上点D ，在此处测得树顶端点B的仰角为 ，且斜坡AF的坡比为1：2.则小明从点A走到点D的过程中，他上升的高度为米；大树BC的高度为米（结果保留根号）.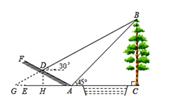
三、解答题
-
19. 某煤矿发生瓦斯爆炸，该地救援队立即赶赴现场进行救援，救援队利用生命探测仪在地面A，B两个探测点探测到C处有生命迹象.已知A，B两点相距6米，探测线与地面的夹角分别是30°和45°，试确定生命所在点C的深度.(精确到0.1米，参考数据： ≈1.41， ≈1.73)
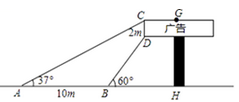
20. 如图，直升飞机在隧道BD上方A点处测得B、D两点的俯角分别为45°和31°。若飞机此时飞行高度AC为1208m，且点C、B、D在同一条直线上，求隧道BD的长（精确到1m）（参考数据：sin31°≈0.52，cos31°≈0.86，tan31°≈0.60）
21. 如图，长方形广告牌架在楼房顶部，边长CD=2m，经测量∠CAH=37°，∠DBH=60°，AB=10m，求GH的长．（参考数据：tan37°≈0.75， ≈1.732，结果精确到0.1m）
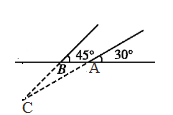
22.如图，某船向正东航行，在A处望见海岛C在北偏东60°，前进6海里到B点，此时测得海岛C在北偏东45°，已知在该岛周围6海里内有暗礁，问船继续向正东航行，有触礁的危险吗?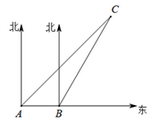
23. 如图，一艘海轮位于灯塔P的北偏东64°方向，距离灯塔120海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，求BP和BA的长(结果取整数). (参考数据： sin64°≈0.90，cos64°≈0.44，tan64°≈2.05， 取1.414)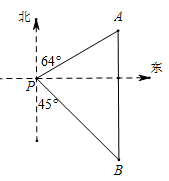
24. 小明学校门前有座山，山上有一电线杆PQ，他很想知道电线杆PQ的高度.于是，有一天，小明和他的同学小亮带着测角器和皮尺来到山下进行测量，测量方案如下：如图，首先，小明站在地面上的点A处，测得电线杆顶端点P的仰角是45°；然后小明向前走6米到达点B处，测得电线杆顶端点P和电线杆底端点Q的仰角分则是60°和30°，设小明的眼睛到地面的距离为1.6米，请根据以上测量的数据，计算电线杆PQ的高度(结果精确到1米，参考数据 =1.7， = 1.4).
25. 被誉为“中原第一高楼”的郑州会展宾馆(俗称“大玉米”)坐落在风景如画的如意湖畔，是来郑州观光的游客留影的最佳景点，学完了三角函数知识后，刘明和王华同学决定用自己学到的知识测量“大玉米”的高度他们制订了测量方案，并利用课余时间完成了实地测量，测量项目及结果如下表
请你帮助该小组根据上表中的测量数据，求出郑州会展宾馆的高度.
(参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，结果保留整数)