广东省广州市南沙区2016-2017学年八年级下学期数学期末考试试卷
试卷更新日期:2017-09-13 类型:期末考试
一、选择题
-
1. 若 有意义,则x的取值范围是( )A、x>1 B、x≥1 C、x>﹣1 D、x≥﹣12. 下列计算正确的是( )A、2 ×3 =6 B、 + = C、3 ﹣ =3 D、 =3. 以下列各组数为边长首尾相连,能构成直角三角形的一组是( )A、2,3,4 B、1,2, C、5,12,17 D、6,8,124. 直角三角形中,两直角边长分别是9和12,则斜边上的中线是( )A、30 B、15 C、 D、5. 如图,在平面直角坐标系中,A(0,0)、B(4,0)、D(1,2)为平行四边形的三个顶点,则第四个顶点C的坐标是( )
 A、(2,5) B、(4,2) C、(5,2) D、(6,2)6. 一次函数y=﹣x+1的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 甲、乙两名同学在参加今年体育中考前各作了5次1分钟跳绳测试,两人的平均成绩相同,所测得成绩的方差分别是S甲2=2.4,S乙2=5.2,那么( )A、甲的成绩更稳定 B、乙的成绩更稳定 C、甲、乙的成绩一样稳定 D、不能确定谁的成绩更稳定8. 如图,菱形ABCD的边长为5,∠ABC=120°,则此菱形ABCD的面积是( )
A、(2,5) B、(4,2) C、(5,2) D、(6,2)6. 一次函数y=﹣x+1的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 甲、乙两名同学在参加今年体育中考前各作了5次1分钟跳绳测试,两人的平均成绩相同,所测得成绩的方差分别是S甲2=2.4,S乙2=5.2,那么( )A、甲的成绩更稳定 B、乙的成绩更稳定 C、甲、乙的成绩一样稳定 D、不能确定谁的成绩更稳定8. 如图,菱形ABCD的边长为5,∠ABC=120°,则此菱形ABCD的面积是( ) A、20 B、25 C、 D、259. 如图,正方形ABCD的边长为4,现有一动点P从点A出发,沿A→B→C→D→A的路径以每秒1个单位长度的速度匀速运动,设点P运动的时间为t,△APB的面积为S,则下列图象能大致反映S与t的函数关系的是( )
A、20 B、25 C、 D、259. 如图,正方形ABCD的边长为4,现有一动点P从点A出发,沿A→B→C→D→A的路径以每秒1个单位长度的速度匀速运动,设点P运动的时间为t,△APB的面积为S,则下列图象能大致反映S与t的函数关系的是( )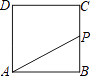 A、
A、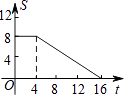 B、
B、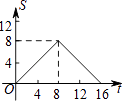 C、
C、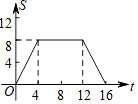 D、
D、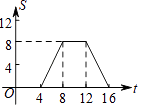 10. 如图,直线y= x﹣4分别与x轴、y轴交于点A和点B,点C、D分别是线段OA、AB的中点,点P为OB上一动点,当PC+PD取最小值时点P的坐标是( )
10. 如图,直线y= x﹣4分别与x轴、y轴交于点A和点B,点C、D分别是线段OA、AB的中点,点P为OB上一动点,当PC+PD取最小值时点P的坐标是( ) A、(0,﹣1) B、(0,﹣2) C、(0,﹣3) D、(0,﹣4)
A、(0,﹣1) B、(0,﹣2) C、(0,﹣3) D、(0,﹣4)二、填空题
-
11. 将直线y=2x向下平移3个单位,得到的直线应为 .12. 实数a在数轴上的位置如图所示,则 = .
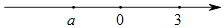 13. 某校规定学生期末综合成绩由三部分组成:期末考成绩占50%,期中考成绩占20%,平时成绩占30%,甲同学某学期的期末考成绩为96分,期中考成绩为85分,平时成绩为90分,则甲同学该学期的期末综合成绩为分.14. 已知点M(1,a)和点N(2,b)是一次函数y=﹣ x﹣1的图象上的两点,则ab(填“>”或“=”或“<”).15. 如图,在矩形ABCD中,对角线AC、BD相交于点O,点E在OC边上,且AB=BE,若∠CBE=20°,则∠COD= .
13. 某校规定学生期末综合成绩由三部分组成:期末考成绩占50%,期中考成绩占20%,平时成绩占30%,甲同学某学期的期末考成绩为96分,期中考成绩为85分,平时成绩为90分,则甲同学该学期的期末综合成绩为分.14. 已知点M(1,a)和点N(2,b)是一次函数y=﹣ x﹣1的图象上的两点,则ab(填“>”或“=”或“<”).15. 如图,在矩形ABCD中,对角线AC、BD相交于点O,点E在OC边上,且AB=BE,若∠CBE=20°,则∠COD= . 16. 如图,已知在正方形ABCD外取一点E,连接CE、BE、DE.过点C作CE的垂线交BE于点F.CE=CF=1,DF= .下列结论:①△BCF≌△DCE;②EB⊥ED;③点D到直线CE的距离为2;④S四边形DECF= + .其中正确结论的序号是 .
16. 如图,已知在正方形ABCD外取一点E,连接CE、BE、DE.过点C作CE的垂线交BE于点F.CE=CF=1,DF= .下列结论:①△BCF≌△DCE;②EB⊥ED;③点D到直线CE的距离为2;④S四边形DECF= + .其中正确结论的序号是 .
三、解答题
-
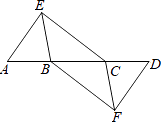
17. 计算:(1)、 ﹣ + ;(2)、( ﹣2)2 .18. 如图,四边形BFCE是平行四边形,点A、B、C、D在同一条直线上,且AB=CD,连接AE、DF.求证:AE=DF.
 19. 某校八年级部分学生利用课外活动时间,积极参加篮球定点投篮的训练,训练结束后进行一次测试,记录如下表:
19. 某校八年级部分学生利用课外活动时间,积极参加篮球定点投篮的训练,训练结束后进行一次测试,记录如下表:进球数(个)
8
7
6
5
4
3
人数
2
2
5
7
9
3
回答下列问题:
(1)、测试记录中,篮球定点投篮进球数的众数是个,中位数是个.(2)、求本次测试的人均进球数.20. 如图,在平面直角坐标系xOy中,直线y1=﹣x+b过点A,且与直线y2=x+3相交于点B(m,2),直线y2=x+3与x轴相交于点C. (1)、求m的值.(2)、求△ABC的面积.(3)、根据图象,直接写出关于x的不等式﹣x+b>x+3的解集.21. 为了推广城市绿色出行,南沙区交委准备在蕉门河沿岸东西走向AB路段建设一个共享单车停放点,该路段附近有两个广场C和D,如图所示,CA⊥AB于A,DB⊥AB于B,AB=3km,CA=2km,DB=1.6km,试问这个单车停放点E应建在距点A多少km处,才能使它到两广场的距离相等.
(1)、求m的值.(2)、求△ABC的面积.(3)、根据图象,直接写出关于x的不等式﹣x+b>x+3的解集.21. 为了推广城市绿色出行,南沙区交委准备在蕉门河沿岸东西走向AB路段建设一个共享单车停放点,该路段附近有两个广场C和D,如图所示,CA⊥AB于A,DB⊥AB于B,AB=3km,CA=2km,DB=1.6km,试问这个单车停放点E应建在距点A多少km处,才能使它到两广场的距离相等. 22. 如图,四边形ABCD是菱形,对角线AC、BD相交于点O,分别延长OB,OD到点E,F,使BE=DF,顺次连接A、E、C、F各点.
22. 如图,四边形ABCD是菱形,对角线AC、BD相交于点O,分别延长OB,OD到点E,F,使BE=DF,顺次连接A、E、C、F各点. (1)、求证:∠FAD=∠EAB.(2)、若∠ADC=130°,要使四边形AECF是正方形,求∠FAD的度数.23. 小明和小红两人周末去爬山,小红先出发,中间休息了一段时间,然后按休息前的进度继续前进,最后比小明迟到达山顶.设他们俩从山脚出发后所用的时间t(分钟)与所走的路程S(米)之间的函数关系如图所示:
(1)、求证:∠FAD=∠EAB.(2)、若∠ADC=130°,要使四边形AECF是正方形,求∠FAD的度数.23. 小明和小红两人周末去爬山,小红先出发,中间休息了一段时间,然后按休息前的进度继续前进,最后比小明迟到达山顶.设他们俩从山脚出发后所用的时间t(分钟)与所走的路程S(米)之间的函数关系如图所示: (1)、根据图象小明登山的速度为米/分,小红的登山速度为米/分.(2)、求出BC段图象的函数关系式,并写出自变量的取值范围.(3)、小明到达山顶后,小红还有多少米到山顶?24. 如图,四边形OABC为矩形,A点在x轴上,C点在y轴上,矩形一角经过翻折后,顶点B落在OA边的点G处,折痕为EF,F点的坐标是(4,1),∠FGA=30°.
(1)、根据图象小明登山的速度为米/分,小红的登山速度为米/分.(2)、求出BC段图象的函数关系式,并写出自变量的取值范围.(3)、小明到达山顶后,小红还有多少米到山顶?24. 如图,四边形OABC为矩形,A点在x轴上,C点在y轴上,矩形一角经过翻折后,顶点B落在OA边的点G处,折痕为EF,F点的坐标是(4,1),∠FGA=30°. (1)、求B点坐标.(2)、求直线EF解析式.(3)、若点M在y轴上,直线EF上是否存在点N,使以M、N、F、G为顶点的四边形是平行四边形?若存在,求N点的坐标;若不存在,请说明理由.
(1)、求B点坐标.(2)、求直线EF解析式.(3)、若点M在y轴上,直线EF上是否存在点N,使以M、N、F、G为顶点的四边形是平行四边形?若存在,求N点的坐标;若不存在,请说明理由.