北京市朝阳区六校2020届高三数学四月联考试卷（B卷)

试卷更新日期：2020-04-27 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知命题 $p$ ： $\forall x \in R$ ， $e^{x} > 1$ ，那么命题 $p$ 的否定为（）

A、 $\exists x_{0} \in R$ ， $e^{x_{0}} \leq 1$ B、 $\forall x \in R$ ， $e^{x} < 1$ C、 $\exists x_{0} \in R$ ， $e^{x_{0}} > 1$ D、 $\forall x \in R$ ， $e^{x} \leq 1$

查看试题解析
2. 设集合 $A = {x \in Z | x^{2} - 3 x - 4 \leq 0}$ ， $B = {x | e^{x - 2} < 1}$ ，则 $A \cap B$ =（）

A、 ${- 1, 0, 1, 2}$ B、 $[- 1, 2)$ C、 ${- 1, 0, 1}$ D、 $[- 1, 2]$

查看试题解析
3. 下列函数中既是奇函数，又在区间 $(0 ， 1)$ 上单调递减的是（）

A、 $f (x) = - x^{3} + 2$ B、 $f (x) = \log_{\frac{1}{2}} | x |$ C、 $f (x) = x^{3} - 3 x$ D、 $f (x) = \sin x$

查看试题解析
4. 已知 $a = \log_{\sqrt{3}} 2$ ， $b = \log_{0 .2} 0.3$ ， $c = \tan \frac{11 π}{3}$ ，则 $a$ ， $b$ ， $c$ 的大小关系是（）

A、 $c < b < a$ B、 $b < a < c$ C、 $c < a < b$ D、 $b < c < a$

查看试题解析

5. 为了宣传今年

9

月即将举办的“第十八届中国西部博览会”（简称“西博会”），组委会举办了“西博会”知识有奖问答活动. 在活动中，组委会对会议举办地参与活动的

15 \sim 65

岁市民进行随机抽样，各年龄段人数情况如下：

组号	分组	各组人数	各组人数频率分布直方图
第 $1$ 组	$[15 ， 25)$	$10$
第 $2$ 组	$[25 ， 35)$	$a$
第 $3$ 组	$[35 ， 45)$	$b$
第 $4$ 组	$[45 ， 55)$	$c$
第 $5$ 组	$[55 ， 65]$	$d$

根据以上图表中的数据可知图表中 $a$ 和 $x$ 的值分别为（）

A、

20

，

0.15

B、

15

，

0.015

C、

20

，

0.015

D、

15

，

0.15

查看试题解析

6. 已知向量 $\vec{a} = (2, 2 \sqrt{3})$ ，若 $\vec{a} \cdot \vec{b} = - \frac{16}{3}$ ，则 $\vec{b}$ 在 $\vec{a}$ 上的投影是（）

A、 $\frac{3}{4}$ B、 $- \frac{3}{4}$ C、 $\frac{4}{3}$ D、 $- \frac{4}{3}$

查看试题解析
7. 某三棱锥的三视图如图所示，则这个三棱锥中最长的棱的长度为（）

A、 $\sqrt{5}$ B、 $3$ C、 $\sqrt{6}$ D、 $2 \sqrt{3}$

查看试题解析
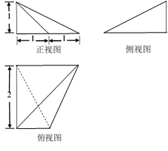8. 已知 $△ A B C$ ，则“ $\sin A = \cos B$ ”是“ $△ A B C$ 是直角三角形”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
9. “杨辉三角”是中国古代重要的数学成就，它比西方的“帕斯卡三角形”早了 $300$ 多年.如图是由“杨辉三角”拓展而成的三角形数阵，记 $a_{n}$ 为图中虚线上的数 $1 ， 3 ， 6 ， 10 ， \cdot \cdot \cdot$ 构成的数列 ${a_{n}}$ 的第 $n$ 项，则 $a_{100}$ 的值为（）

A、5049 B、5050 C、5051 D、5101

查看试题解析
10. 关于函数 $f (x) = (x^{2} + a x - 1) e^{x}$ ，有以下三个结论：①函数恒有两个零点，且两个零点之积为 $- 1$ ；②函数的极值点不可能是 $- 1$ ；③函数必有最小值.其中正确结论的个数有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析

二、填空题

11. 在 ${(x - \frac{2}{x})}^{5}$ 的二项展开式中， $x^{- 3}$ 的系数为.（用数字作答）

查看试题解析
12. 设无穷等比数列 ${a_{n}}$ 的各项为整数，公比为 $q$ ，且 $| q | \neq 1$ ， $a_{1} + a_{3} < 2 a_{2}$ ，写出数列 ${a_{n}}$ 的一个通项公式.

查看试题解析
13. 在平面直角坐标系中，已知点 $A (0 ， 1)$ ， $B (1 ， 1)$ ， $P$ 为直线 $A B$ 上的动点， $A$ 关于直线 $O P$ 的对称点记为 $Q$ ，则线段 $B Q$ 的长度的最大值是.

查看试题解析
14. 关于曲线 $C : x^{2} - x y + y^{2} = 4$ ，给出下列三个结论：
① 曲线 $C$ 关于原点对称，但不关于 $x$ 轴、 $y$ 轴对称；② 曲线 $C$ 恰好经过4个整点（即横、纵坐标均为整数的点）；③ 曲线 $C$ 上任意一点到原点的距离都不大于 $2 \sqrt{2}$ .其中，正确结论的序号是.

查看试题解析

三、双空题

15. 已知复数 $z$ 在复平面内对应的点位于第一象限，且满足 $| z | = 5$ ， $z + \bar{z} = 6$ ，则 $z$ 的实部为，虚部为.

查看试题解析

四、解答题

16. 已知：①函数 $f (x) = \cos ω x \sin (ω x + \frac{π}{6}) - \frac{1}{4} (ω > 0)$ ；
②向量 $\vec{m} = (\sqrt{3} \sin ω x, \cos 2 ω x)$ ， $\vec{n} = (\frac{1}{2} \cos ω x, \frac{1}{4})$ ，且 $ω > 0$ ， $f (x) = \vec{m} \cdot \vec{n}$ ；

③函数 $f (x) = \frac{1}{2} \sin (2 ω x + φ) (ω > 0, | φ | < \frac{π}{2})$ 的图象经过点 $(\frac{π}{6}, \frac{1}{2})$

请在上述三个条件中任选一个，补充在下面问题中，并解答.

已知_________________，且函数 $f (x)$ 的图象相邻两条对称轴之间的距离为 $\frac{π}{2}$ .

(1)、若 $0 < θ < \frac{π}{2}$ ，且 $\sin θ = \frac{1}{2}$ ，求 $f (θ)$ 的值；

(2)、求函数 $f (x)$ 在 $[0, 2 π]$ 上的单调递减区间.
注：如果选择多个条件分别解答，按第一个解答计分.

查看试题解析
17. 体温是人体健康状况的直接反应，一般认为成年人腋下温度 $T$ （单位： $° C$ ）平均在 $36 ° C \sim 37 ° C$ 之间即为正常体温，超过 $37.1 ° C$ 即为发热.发热状态下，不同体温可分成以下三种发热类型：低热： $37.1 \leq T \leq 38$ ；高热： $38 < T \leq 40$ ；超高热（有生命危险）： $T > 40$ .
某位患者因患肺炎发热，于12日至26日住院治疗. 医生根据病情变化，从14日开始，以3天为一个疗程，分别用三种不同的抗生素为该患者进行消炎退热. 住院期间，患者每天上午8：00服药，护士每天下午16：00为患者测量腋下体温记录如下：

(1)、请你计算住院期间该患者体温不低于 $39 ° C$ 的各天体温平均值；

(2)、在 $19$ 日— $23$ 日期间，医生会随机选取 $3$ 天在测量体温的同时为该患者进行某一特殊项目“ $α$ 项目”的检查，记 $X$ 为高热体温下做“ $α$ 项目”检查的天数，试求 $X$ 的分布列与数学期望；

(3)、抗生素治疗一般在服药后2-8个小时就能出现血液浓度的高峰，开始杀灭细菌，达到消炎退热效果.假设三种抗生素治疗效果相互独立，请依据表中数据，判断哪种抗生素治疗效果最佳，并说明理由.

查看试题解析
18. 在四棱锥 $P - A B C D$ 中，平面 $P A D ⊥$ 平面 $A B C D$ .底面 $A B C D$ 为梯形， $A B / / C D$ ， $A B ⊥ A D$ ，且 $A B = 1$ ， $P A = A D = D C = 2$ ， $P D = 2 \sqrt{2}$ .

(1)、求证： $A B ⊥ P D$ ；

(2)、求二面角 $P - B C - D$ 的余弦值；

(3)、若 $M$ 是棱 $P A$ 的中点，求证：对于棱 $B C$ 上任意一点 $F$ ， $M F$ 与 $P C$ 都不平行.

查看试题解析
19. 已知椭圆 $C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{1}{2}$ ，过椭圆右焦点 $F$ 的直线 $l$ 与椭圆交于 $A$ ， $B$ 两点，当直线 $l$ 与 $x$ 轴垂直时， $| A B | = 3$ .

(1)、求椭圆 $C$ 的标准方程；

(2)、当直线 $l$ 与 $x$ 轴不垂直时，在 $x$ 轴上是否存在一点 $P$ （异于点 $F$ ），使 $x$ 轴上任意点到直线 $P A$ ， $P B$ 的距离均相等？若存在，求 $P$ 点坐标；若不存在，请说明理由.

查看试题解析
20. 已知函数 $f (x) = e^{x} - a x^{2} (a \in R)$ .

(1)、若曲线 $y = f (x)$ 在 $(1 ， f (1))$ 处的切线与 $x$ 轴平行，求 $a$ ；

(2)、已知 $f (x)$ 在 $[0 ， 1]$ 上的最大值不小于 $2$ ，求 $a$ 的取值范围；

(3)、写出 $f (x)$ 所有可能的零点个数及相应的 $a$ 的取值范围.（请直接写出结论）

查看试题解析
21. 已知集合 $S_{n} = {X | X = (x_{1}, x_{2}, \dots, x_{n}), x_{i} \in {0, 1}, i = 1, 2, \dots, n} (n \geq 2)$ ，对于 $A = (a_{1}, a_{2}, \dots, a_{n})$ $\in S_{n}$ ， $B = (b_{1}, b_{2}, \dots, b_{n}) \in S_{n}$ ，定义 $A$ 与 $B$ 的差为 $A - B = (| a_{1} - b_{1} |, | a_{2} - b_{2} |, \dots, | a_{n} - b_{n} |)$ ； $A$ 与 $B$ 之间的距离为 $d (A, B) = | a_{1} - b_{1} | + | a_{2} - b_{2} | + \dots + | a_{n} - b_{n} |$ .

(1)、若 $A - B = (0, 1)$ ，试写出所有可能的 $A$ ， $B$ ；

(2)、 $\forall A, B, C \in S_{n}$ ，证明： $d (A - C, B - C) = d (A, B)$ ；

(3)、 $\forall A, B, C \in S_{n}$ ， $d (A, B), d (A, C), d (B, C)$ 三个数中是否一定有偶数？证明你的结论.

查看试题解析