江西省九江市赣北中考联盟2019年中考数学模拟考试试卷
试卷更新日期:2020-04-26 类型:中考模拟
一、单选题
-
1. ﹣2的绝对值是( )A、2 B、 C、 D、2. 下列计算正确是( )A、 B、(a﹣b)2=a2﹣b2 C、a2+a3=a5 D、(2a2b3)3=﹣6a6b33. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
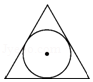 B、
B、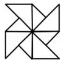 C、
C、 D、
D、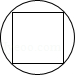 4. 小明用手机软件记录了最近30天的运动步数,并将记录结果制作成了如下统计表:
4. 小明用手机软件记录了最近30天的运动步数,并将记录结果制作成了如下统计表:步数/万步
1.1
1.2
1.3
1.4
1.5
天数
3
9
5
a
b
小明这30天平均每天走1.3万步,在每天所走的步数中,众数和中位数分别是( )
A、1.3,1.3 B、1.4,1.3 C、1.4,1.4 D、1.3,1.45. 如图是二次函数 的图象,有下面四个结论: ; ; ; ,其中正确结论是( ) A、 B、 C、 D、6. 如图,正方形ABCD中,AB=3,点E是对角线AC上的一点,连接DE , 过点E作EF⊥DE , 交AB于点F , 连接DF交AC于点G , 下列结论:
A、 B、 C、 D、6. 如图,正方形ABCD中,AB=3,点E是对角线AC上的一点,连接DE , 过点E作EF⊥DE , 交AB于点F , 连接DF交AC于点G , 下列结论:①DE=EF;②∠ADF=∠AEF;③DG2=GE•GC;④若AF=1,则EG= ,其中结论正确个数是( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
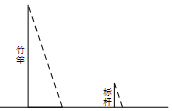
7. 分解因式:8. 2019年3月5日召开十三届全国人大二次会议,政府工作报告中提到2012年我国的贫困人口为9899万人,2018年减少到1660万人,连续6年平均每年减贫1300多万人,将数据1300万用科学记数法可表示为 .9. 已知a , b是一元二次方程x2+x﹣4=0的两个不相等的实数根,则a2﹣b= .10. 《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:“今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?”意思就是:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆(如图所示),它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为 .
 11. 如图,在平面直角坐标系xOy中,等边△AOB的边长为10,点C在边OA上,点D在边AB上,且OC=3BD . 反比例函数y= (k≠0)的图象恰好经过C、D两点,则k的值为 .
11. 如图,在平面直角坐标系xOy中,等边△AOB的边长为10,点C在边OA上,点D在边AB上,且OC=3BD . 反比例函数y= (k≠0)的图象恰好经过C、D两点,则k的值为 . 12. 如图,已知△ABC中,AB=AC=5,BC=8,将△ABC沿射线BC方向平移m个单位得到△DEF,顶点A,B,C分别与D,E,F对应,若以A,D,E为顶点的三角形是等腰三角形,且AE为腰,则m的值是 .
12. 如图,已知△ABC中,AB=AC=5,BC=8,将△ABC沿射线BC方向平移m个单位得到△DEF,顶点A,B,C分别与D,E,F对应,若以A,D,E为顶点的三角形是等腰三角形,且AE为腰,则m的值是 .
三、解答题
-
13.(1)、先化简 ,再选择一个合适的x值代入求值.(2)、如图所示,已知点A , D , B , E在同一条直线上,且AD=BE , BC=EF , ∠ABC=∠DEF , 求证:AC∥DF .
 14. 解不等式组: 并将该不等式的解集在数轴上表示出来.15. 如图,在▱ABCD中,点E为边BC上的中点,请仅用无刻度的直尺,按要求画图(保留画图痕迹,不写画法).
14. 解不等式组: 并将该不等式的解集在数轴上表示出来.15. 如图,在▱ABCD中,点E为边BC上的中点,请仅用无刻度的直尺,按要求画图(保留画图痕迹,不写画法). (1)、在图1中,作EF∥AB交AD于点F;(2)、在图2中,若AB=BC , 作一矩形,使得其面积等于▱ABCD的一半.16. 为了响应国家有关开展中小学生“课后服务”的政策,某学校课后开设了A:课后作业辅导、B:书法、C:阅读、D:绘画、E:器乐,五门课程供学生选择;其中A(必选项目),再从B、C、D、E中选两门课程.(1)、若学生小玲第一次选一门课程,直接写出学生小玲选中项目E的概率;(2)、若学生小强和小明在选项的过程中,第一次都是选了项目E , 那么他俩第二次同时选择书法或绘画的概率是多少?请用列表法或画树状图的方法加以说明并列出所有等可能的结果.17. 如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y= 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO= ,OB=4,OE=2.
(1)、在图1中,作EF∥AB交AD于点F;(2)、在图2中,若AB=BC , 作一矩形,使得其面积等于▱ABCD的一半.16. 为了响应国家有关开展中小学生“课后服务”的政策,某学校课后开设了A:课后作业辅导、B:书法、C:阅读、D:绘画、E:器乐,五门课程供学生选择;其中A(必选项目),再从B、C、D、E中选两门课程.(1)、若学生小玲第一次选一门课程,直接写出学生小玲选中项目E的概率;(2)、若学生小强和小明在选项的过程中,第一次都是选了项目E , 那么他俩第二次同时选择书法或绘画的概率是多少?请用列表法或画树状图的方法加以说明并列出所有等可能的结果.17. 如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y= 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO= ,OB=4,OE=2. (1)、求反比例函数的解析式;(2)、若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF.如果S△BAF=4S△DFO , 求点D的坐标.18. 为更精准地关爱留守学生,某学校将留守学生的各种情形分成四种类型:A.由父母一方照看;B.由爷爷奶奶照看;C.由叔姨等近亲照看;D.直接寄宿学校.某数学小组随机调查了一个班级,发现该班留守学生数量占全班总人数的20%,并将调查结果制成如下两幅不完整的统计图.
(1)、求反比例函数的解析式;(2)、若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF.如果S△BAF=4S△DFO , 求点D的坐标.18. 为更精准地关爱留守学生,某学校将留守学生的各种情形分成四种类型:A.由父母一方照看;B.由爷爷奶奶照看;C.由叔姨等近亲照看;D.直接寄宿学校.某数学小组随机调查了一个班级,发现该班留守学生数量占全班总人数的20%,并将调查结果制成如下两幅不完整的统计图. (1)、该班共有名留守学生,B类型留守学生所在扇形的圆心角的度数为;(2)、将条形统计图补充完整;(3)、已知该校共有2400名学生,现学校打算对D类型的留守学生进行手拉手关爱活动,请你估计该校将有多少名留守学生在此关爱活动中受益?19. 如图(1)是一款手机支架,忽略支管的粗细,得到它的简化结构图如图(2)所示.已知支架底部支架CD平行于水平面,EF⊥OE , GF⊥EF , 支架可绕点O旋转,OE=20cm , EF=20 cm . 如图(3)若将支架上部绕O点逆时针旋转,当点G落在直线CD上时,测量得∠EOG=65°.
(1)、该班共有名留守学生,B类型留守学生所在扇形的圆心角的度数为;(2)、将条形统计图补充完整;(3)、已知该校共有2400名学生,现学校打算对D类型的留守学生进行手拉手关爱活动,请你估计该校将有多少名留守学生在此关爱活动中受益?19. 如图(1)是一款手机支架,忽略支管的粗细,得到它的简化结构图如图(2)所示.已知支架底部支架CD平行于水平面,EF⊥OE , GF⊥EF , 支架可绕点O旋转,OE=20cm , EF=20 cm . 如图(3)若将支架上部绕O点逆时针旋转,当点G落在直线CD上时,测量得∠EOG=65°. (1)、求FG的长度(结果精确到0.1);(2)、将支架由图(3)转到图(4)的位置,若此时F、O两点所在的直线恰好于CD垂直,点F的运动路线的长度称为点F的路径长,求点F的路径长.
(1)、求FG的长度(结果精确到0.1);(2)、将支架由图(3)转到图(4)的位置,若此时F、O两点所在的直线恰好于CD垂直,点F的运动路线的长度称为点F的路径长,求点F的路径长.(参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14,1.73)
20. 如图,⊙O是△ABC的外接圆,∠C=60°,AD是⊙O的直径,Q是AD延长线上的一点,且BQ=AB . (1)、求证:BQ是⊙O的切线;(2)、若AQ=6.
(1)、求证:BQ是⊙O的切线;(2)、若AQ=6.①求⊙O的半径;
②P是劣弧AB上的一个动点,过点P作EF∥AB , EF分别交CA、CB的延长线于E、F两点,连接OP , 当OP和AB之间是什么位置关系时,线段EF取得最大值?判断并说明理由.
21. 为拓宽学生视野,我市某中学决定组织部分师生去庐山西海开展研学旅行活动,在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生.为了安全,既要保证所有师生都有车坐,又要保证每辆客车上至少要有2名老师.现有甲、乙两种大客车,它们的载客量和租金如表所示.甲种客车
乙种客车
载客量/(人/辆)
30
42
租金/(元/辆)
300
400
(1)、参加此次研学旅行活动的老师和学生各有多少人?租用客车总数为多少辆?(2)、设租用x辆乙种客车,租车总费用为w元,请写出w与x之间的函数关系式;(3)、在(2)的条件下,学校计划此次研学旅行活动的租车总费用不超过3100元,租用乙种客车不少5辆,你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.22. 已知二次函数y=ax2﹣2ax﹣2的图象(记为抛物线C1)顶点为M , 直线l:y=2x﹣a与x轴,y轴分别交于A , B .(1)、对于抛物线C1 , 以下结论正确是;①对称轴是:直线x=1;②顶点坐标(1,﹣a﹣2);③抛物线一定经过两个定点.
(2)、当a>0时,设△ABM的面积为S , 求S与a的函数关系;(3)、将二次函数y=ax2﹣2ax﹣2的图象C1绕点P(t , ﹣2)旋转180°得到二次函数的图象(记为抛物线C2),顶点为N .①当﹣2≤x≤1时,旋转前后的两个二次函数y的值都会随x的增大而减小,求t的取值范围;
②当a=1时,点Q是抛物线C1上的一点,点Q在抛物线C2上的对应点为Q',试探究四边形QMQ'N能否为正方形?若能,求出t的值,若不能,请说明理由.
23. 【操作发现】如图①,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.
 (1)、请按要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′;(2)、在(1)所画图形中,∠AB′B= .
(1)、请按要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′;(2)、在(1)所画图形中,∠AB′B= .