江西省吉安市吉州区2019年中考数学5月模拟考试试卷
试卷更新日期:2020-04-26 类型:中考模拟
一、单选题
-
1. 2019的绝对值等于( )A、 ﹣2019 B、2019 C、﹣ D、2. 如图几何体的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 今年3月,某校举行“唱红歌”歌咏比赛,有19位同学参加选拔赛,所得分数互不相同,按成绩取前9名进入决赛,若知道某同学分数,要判断他能否进入决赛,只需知道19位同学分数的( )A、中位数 B、平均数 C、极差 D、方差4. 欧阳修在《卖油翁》中写道:“(翁)乃取一葫芦置于地,以钱覆其口,徐以构酌油之,自钱孔入,而钱不湿”,如图,可见卖油的技艺之高超,若铜钱直径4cm , 中间x有边长为1cm的正方形小孔,随机向铜色钱上滴一滴油(油滴大小忽略不计),则油恰好落入孔中的概率是( )
3. 今年3月,某校举行“唱红歌”歌咏比赛,有19位同学参加选拔赛,所得分数互不相同,按成绩取前9名进入决赛,若知道某同学分数,要判断他能否进入决赛,只需知道19位同学分数的( )A、中位数 B、平均数 C、极差 D、方差4. 欧阳修在《卖油翁》中写道:“(翁)乃取一葫芦置于地,以钱覆其口,徐以构酌油之,自钱孔入,而钱不湿”,如图,可见卖油的技艺之高超,若铜钱直径4cm , 中间x有边长为1cm的正方形小孔,随机向铜色钱上滴一滴油(油滴大小忽略不计),则油恰好落入孔中的概率是( ) A、 B、 C、 D、5. 已知二次函数y=2mx2+(1﹣m)x﹣1﹣m , 下面说法不正确是( )A、当m=1时,函数图象的顶点坐标是(0,﹣2) B、当m=﹣1时,函数图象与x轴有两个交点 C、函数图象经过定点(1,0),(﹣ ,﹣ ) D、当m>0时,函数图象截x轴所得的线段长度小于6. 如图,在正方形 中, , 分别为 , 的中点, 为对角线 上的一个动点,则下列线段的长等于 最小值的是( )
A、 B、 C、 D、5. 已知二次函数y=2mx2+(1﹣m)x﹣1﹣m , 下面说法不正确是( )A、当m=1时,函数图象的顶点坐标是(0,﹣2) B、当m=﹣1时,函数图象与x轴有两个交点 C、函数图象经过定点(1,0),(﹣ ,﹣ ) D、当m>0时,函数图象截x轴所得的线段长度小于6. 如图,在正方形 中, , 分别为 , 的中点, 为对角线 上的一个动点,则下列线段的长等于 最小值的是( )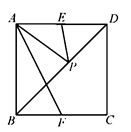 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 的立方根是 .
三、填空题
-
8. 3月5日,第十三届全国人大二次会议上国务院总理李克强在《政府工作报告》中指出:过去的一年里中国的精准脱贫推进有力,农村贫困人口减少1386万.其中数据13860000用科学记数法表示为 .9. 夏季来临,某超市试销A、B两种型号的风扇,两周内共销售30台,销售收入5300元,A型风扇每台200元,B型风扇每台150元,问A、B两种型号的风扇分别销售了多少台?若设A型风扇销售了x台,B型风扇销售了y台,则根据题意列出方程组 .10. 如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1 , 若点B1在线段BC的延长线上,则∠BB1C1的大小是度.
 11. 在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m . 其行走路线如图所示,第1次移动到A1 , 第2次移动到A2…,第n次移动到An , 则△OA2A2019的面积是 .
11. 在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m . 其行走路线如图所示,第1次移动到A1 , 第2次移动到A2…,第n次移动到An , 则△OA2A2019的面积是 . 12. Rt△ABC中,∠ABC=90°,AB=3,BC=4,过点B的直线把△ABC分割成两个三角形,使其中只有一个是等腰三角形,则这个等腰三角形的面积是 .
12. Rt△ABC中,∠ABC=90°,AB=3,BC=4,过点B的直线把△ABC分割成两个三角形,使其中只有一个是等腰三角形,则这个等腰三角形的面积是 .四、解答题
-
13.(1)、解不等式组:(2)、如图,将△ABC沿BC方向平移2cm得到△DEF , 若△ABC的周长为16cm , 求四边形ABFD的周长.
 14. 先化简,再求值:(xy2+x2y)× ,其中x=π0﹣( )﹣1 , y=2sin45°﹣ .15. 在不透明的袋子中有四张标着数字1,2,3,4的卡片,这些卡片除数字外都相同.小芸同学按照一定的规则抽出两张卡片,并把卡片上的数字相加.如图是她所画的树状图的一部分.
14. 先化简,再求值:(xy2+x2y)× ,其中x=π0﹣( )﹣1 , y=2sin45°﹣ .15. 在不透明的袋子中有四张标着数字1,2,3,4的卡片,这些卡片除数字外都相同.小芸同学按照一定的规则抽出两张卡片,并把卡片上的数字相加.如图是她所画的树状图的一部分. (1)、由如图分析,小芸的游戏规则是:从袋子中随机抽出一张卡片后(填“放回”或“不放回”),再随机抽出一张卡片;(2)、帮小芸完成树状图;(3)、求小芸两次抽到的数字之和为奇数的概率.16. 图①、图②都是由边长为1的小菱形构成的网格,每个小菱形的顶点称为格点.点O , M , N , A , B均在格点上,请仅用无刻度直尺在网格中完成下列画图.
(1)、由如图分析,小芸的游戏规则是:从袋子中随机抽出一张卡片后(填“放回”或“不放回”),再随机抽出一张卡片;(2)、帮小芸完成树状图;(3)、求小芸两次抽到的数字之和为奇数的概率.16. 图①、图②都是由边长为1的小菱形构成的网格,每个小菱形的顶点称为格点.点O , M , N , A , B均在格点上,请仅用无刻度直尺在网格中完成下列画图. (1)、在图①中,画出∠MON的平分线OP;(2)、在图②中,画一个Rt△ABC , 使点C在格点上.17. 如图为放置在水平桌面上的台灯的平面示意图,灯臂AO长为40cm,与水平面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°,求该台灯照亮水平面的宽度BC(不考虑其他因素,结果精确到0.1cm.温馨提示:sin75°≈0.97,cos75°≈0.26, ).
(1)、在图①中,画出∠MON的平分线OP;(2)、在图②中,画一个Rt△ABC , 使点C在格点上.17. 如图为放置在水平桌面上的台灯的平面示意图,灯臂AO长为40cm,与水平面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°,求该台灯照亮水平面的宽度BC(不考虑其他因素,结果精确到0.1cm.温馨提示:sin75°≈0.97,cos75°≈0.26, ).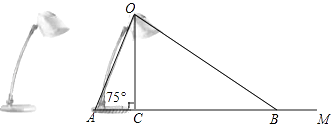 18. 目前“微信”、“支付宝”、“共享单车”和“网购”给我们带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行了调查,随机调查了 人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
18. 目前“微信”、“支付宝”、“共享单车”和“网购”给我们带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行了调查,随机调查了 人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.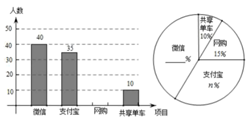 (1)、根据图中信息求出 = , =;(2)、请你帮助他们将这两个统计图补全;(3)、根据抽样调查的结果,请估算全校2000名学生种,大约有多少人最认可“微信”这一新生事物?19. 如图,已知AB是⊙O上的点,C是⊙O上的点,点D在AB的延长线上,∠BCD=∠BAC.
(1)、根据图中信息求出 = , =;(2)、请你帮助他们将这两个统计图补全;(3)、根据抽样调查的结果,请估算全校2000名学生种,大约有多少人最认可“微信”这一新生事物?19. 如图,已知AB是⊙O上的点,C是⊙O上的点,点D在AB的延长线上,∠BCD=∠BAC.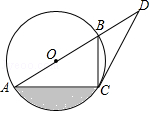 (1)、求证:CD是⊙O的切线;(2)、若∠D=30°,BD=2,求图中阴影部分的面积.20. 在某水果店一次性购买A种水果的单价y(元)与购买量x(千克)的函数关系如图.
(1)、求证:CD是⊙O的切线;(2)、若∠D=30°,BD=2,求图中阴影部分的面积.20. 在某水果店一次性购买A种水果的单价y(元)与购买量x(千克)的函数关系如图. (1)、下列关于三段函数图象的说法不正确是( )
(1)、下列关于三段函数图象的说法不正确是( )A、第①段函数图象表示数量不多于5千克时,单价为10元.
B、第③段函数图象表示数量不少于11千克时,单价为8.8元.
C、第②段函数图象可知:当一次性数量多于5千克但不多于11千克时,每多买1千克,单价就降低1.2元.
(2)、求图中第②段函数图象的解析式,并指出x的取值范围.(3)、某天老李计划用90元去该店买A种水果,问老李一次性(或最多)能买回多少千克A种水果?21. 已知:如图,正比例函数 的图象与反比例函数 的图象交于点 (1)、试确定上述正比例函数和反比例函数的表达式;(2)、根据图象回答,在第一象限内,当 取何值时,反比例函数的值大于正比例函数的值?(3)、 是反比例函数图象上的一动点,其中 过点 作直线 轴,交 轴于点 ;过点 作直线 轴交 轴于点 ,交直线 于点 .当四边形 的面积为6时,请判断线段 与 的大小关系,并说明理由.22. 如图,抛物线C1与抛物线C2与x轴有相同的交点M , N(点M在点N的左侧),与x轴的交点分别为A , B , 且点A的坐标为(0,﹣3),抛物线C2的解析式为y=mx2+4mx﹣12m(m>0).
(1)、试确定上述正比例函数和反比例函数的表达式;(2)、根据图象回答,在第一象限内,当 取何值时,反比例函数的值大于正比例函数的值?(3)、 是反比例函数图象上的一动点,其中 过点 作直线 轴,交 轴于点 ;过点 作直线 轴交 轴于点 ,交直线 于点 .当四边形 的面积为6时,请判断线段 与 的大小关系,并说明理由.22. 如图,抛物线C1与抛物线C2与x轴有相同的交点M , N(点M在点N的左侧),与x轴的交点分别为A , B , 且点A的坐标为(0,﹣3),抛物线C2的解析式为y=mx2+4mx﹣12m(m>0).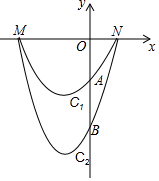 (1)、求M , N两点的坐标;(2)、在第三象限内的抛物线C1上是否存在一点P , 使得△PAM的面积最大,若存在,求出△PAM的面积的最大值;若不存在,说明理由;(3)、设抛物线C2的顶点为点D , 顺次连接A , D , B , N , 若四边形ADBN是平行四边形,求m的值.23. 我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.
(1)、求M , N两点的坐标;(2)、在第三象限内的抛物线C1上是否存在一点P , 使得△PAM的面积最大,若存在,求出△PAM的面积的最大值;若不存在,说明理由;(3)、设抛物线C2的顶点为点D , 顺次连接A , D , B , N , 若四边形ADBN是平行四边形,求m的值.23. 我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.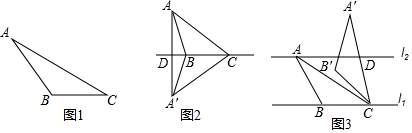 (1)、概念理解:
(1)、概念理解:如图1,在△ABC中,AC=6,BC=3,∠ACB=30°,试判断△ABC是否是”等高底”三角形,请说明理由.
(2)、问题探究:如图2,△ABC是“等高底”三角形,BC是”等底”,作△ABC关于BC所在直线的对称图形得到△A'BC , 连结AA′交直线BC于点D . 若点B是△AA′C的重心,求 的值.
(3)、应用拓展:如图3,已知l1∥l2 , l1与l2之间的距离为2.“等高底”△ABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的 倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C , A′C所在直线交l2于点D . 求CD的值.
-