江西省赣州市2019年中考数学一模考试试卷
试卷更新日期:2020-04-26 类型:中考模拟
一、单选题
-
1. 在平面直角坐标系中,点 (-1,m2+1)一定在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 化简(-2a) a-(-2a)2的结果是( )A、0 B、 C、 D、3. 在数轴上,点A所表示的实数为3,点B所表示的实数为a,⊙A的半径为2,下列说法中不正确是( )A、当1<a<5时,点B在⊙A内 B、当a<5时,点B在⊙A内 C、当a<1时,点B在⊙A外 D、当a>5时,点B在⊙A外4. 如图,分别是由若干个完全相同的小正方体组成的一个几何体的主视图和俯视图,则组成这个几何体的小正方体的个数是( )
 A、2个或3个 B、3个或4个 C、4个或5个 D、5个或6个5. 设有反比例函数 ,(x1 , y1)、(x2 , y2)为其图象上的两点,若x1<0<x2时y1>y2 , 则k的取值范围是( )A、k>0 B、k<0 C、k>﹣1 D、k<﹣16. 如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是( )
A、2个或3个 B、3个或4个 C、4个或5个 D、5个或6个5. 设有反比例函数 ,(x1 , y1)、(x2 , y2)为其图象上的两点,若x1<0<x2时y1>y2 , 则k的取值范围是( )A、k>0 B、k<0 C、k>﹣1 D、k<﹣16. 如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是( ) A、
A、 B、
B、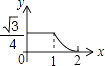 C、
C、 D、
D、
二、填空题
-
7. 据相关报道,近5年中国农村年均脱贫1370万人.1370万可用科学记数法表示为 .8. 不等式组 的解集是 .9. 分解因式:x3﹣x= .10. 如图,在△ABC中,点P是△ABC的内心,则∠PBC+∠PCA+∠PAB=度.
 11. 如图,把正方形铁片OABC置于平面直角坐标系中,顶点A的坐标为(3,0),点P(1,2)在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°,第一次旋转至图①位置,第二次旋转至图②位置…,则正方形铁片连续旋转2017次后,点P的坐标为 .
11. 如图,把正方形铁片OABC置于平面直角坐标系中,顶点A的坐标为(3,0),点P(1,2)在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°,第一次旋转至图①位置,第二次旋转至图②位置…,则正方形铁片连续旋转2017次后,点P的坐标为 . 12. 平面内有四个点A、O、B、C,其中∠AOB=1200 , ∠ACB=600 , AO=BO=2,则满足题意的OC长度为整数的值可以是 .
12. 平面内有四个点A、O、B、C,其中∠AOB=1200 , ∠ACB=600 , AO=BO=2,则满足题意的OC长度为整数的值可以是 .三、解答题
-
13.(1)、解方程:(2)、计算:14.(1)、如图1,点P是正方形ABCD内的一点,把△ABP绕点B顺时针方向旋转,使点A与点C重合,点P的对应点是Q.若PA=3,PB=2 ,PC=5,求∠BQC的度数.
 (2)、点P是等边三角形ABC内的一点,若PA=12,PB=5,PC=13,求∠BPA的度数.15. 如图,在△ABC中,AB=AC , BD⊥AC于点D , CE⊥AB于点E , BD与CE相交于点O , 请仅用无刻度的直尺,分别按下列要求作图.(保留作图痕迹,不写作法)
(2)、点P是等边三角形ABC内的一点,若PA=12,PB=5,PC=13,求∠BPA的度数.15. 如图,在△ABC中,AB=AC , BD⊥AC于点D , CE⊥AB于点E , BD与CE相交于点O , 请仅用无刻度的直尺,分别按下列要求作图.(保留作图痕迹,不写作法) (1)、在图①中作线段BC的中点P;(2)、在图②中,在OB , OC上分别取点M , N , 使MN∥BC .16. 如图,过点A(2,0)的两条直线 , 分别交y轴于B,C,其中点B在原点上方,点C在原点下方,已知AB= .
(1)、在图①中作线段BC的中点P;(2)、在图②中,在OB , OC上分别取点M , N , 使MN∥BC .16. 如图,过点A(2,0)的两条直线 , 分别交y轴于B,C,其中点B在原点上方,点C在原点下方,已知AB= . (1)、求点B的坐标;(2)、若△ABC的面积为4,求 的解析式.17. 深圳市政府计划投资1.4万亿元实施东进战略.为了解深圳市民对东进战略的关注情况.某校数学兴趣小组随机采访部分深圳市民,对采访情况制作了统计图表的一部分如下:
(1)、求点B的坐标;(2)、若△ABC的面积为4,求 的解析式.17. 深圳市政府计划投资1.4万亿元实施东进战略.为了解深圳市民对东进战略的关注情况.某校数学兴趣小组随机采访部分深圳市民,对采访情况制作了统计图表的一部分如下:关注情况
频数
频率
A . 高度关注
m
0.1
B . 一般关注
100
0.5
C . 不关注
30
n
D . 不知道
50
0.25
 (1)、根据上述统计图可得此次采访的人数为人,m= , n=;(2)、根据以上信息补全条形统计图;(3)、根据上述采访结果,请估计在15000名深圳市民中,高度关注东进战略的深圳市民约有人.18. 某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)
(1)、根据上述统计图可得此次采访的人数为人,m= , n=;(2)、根据以上信息补全条形统计图;(3)、根据上述采访结果,请估计在15000名深圳市民中,高度关注东进战略的深圳市民约有人.18. 某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)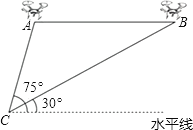 19. 在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.(1)、先从袋子中取出m(m>1)个红球,再从袋子中随机摸出一个球,将“摸出黑球”记为事件A.请完成下列表格:
19. 在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.(1)、先从袋子中取出m(m>1)个红球,再从袋子中随机摸出一个球,将“摸出黑球”记为事件A.请完成下列表格:事件A
必然事件
随机事件
m的值
(2)、先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出一个球是黑球的概率等于 ,求m的值.20. 如图,等腰梯形ABCD放置在平面直角坐标系中,已知 、 、 ,反比例函数的图象经过点C . (1)、求点C坐标和反比例函数的解析式;(2)、将等腰梯形ABCD向上平移m个单位后,使点B恰好落在双曲线上,求m的值.21. 如图,已知⊙O的半径为2,AB为直径,CD为弦,AB与CD交于点M,将弧CD沿着CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,链接PC.
(1)、求点C坐标和反比例函数的解析式;(2)、将等腰梯形ABCD向上平移m个单位后,使点B恰好落在双曲线上,求m的值.21. 如图,已知⊙O的半径为2,AB为直径,CD为弦,AB与CD交于点M,将弧CD沿着CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,链接PC. (1)、求CD的长;(2)、求证:PC是⊙O的切线;(3)、点G为弧ADB的中点,在PC延长线上有一动点Q,连接QG交AB于点E,交弧BC于点F(F与B、C不重合).问GE▪GF是否为定值?如果是,求出该定值;如果不是,请说明理由.22. 若抛物线L:y=ax2+bx+c(a,b,c是常数,abc≠0)与直线l都经过y轴上的一点P,且抛物线L的顶点Q在直线l上,则称此直线l与该抛物线L具有“一带一路”关系.此时,直线l叫做抛物线L的“带线”,抛物线L叫做直线l的“路线”.(1)、若直线y=mx+1与抛物线y=x2﹣2x+n具有“一带一路”关系,求m,n的值;(2)、若某“路线”L的顶点在反比例函数y= 的图象上,它的“带线”l的解析式为y=2x﹣4,求此“路线”L的解析式;(3)、当常数k满足 ≤k≤2时,求抛物线L:y=ax2+(3k2﹣2k+1)x+k的“带线”l与x轴,y轴所围成的三角形面积的取值范围.23. 课题:两个重叠的正多边形,其中的一个绕某一顶点旋转所形成的有关问题.
(1)、求CD的长;(2)、求证:PC是⊙O的切线;(3)、点G为弧ADB的中点,在PC延长线上有一动点Q,连接QG交AB于点E,交弧BC于点F(F与B、C不重合).问GE▪GF是否为定值?如果是,求出该定值;如果不是,请说明理由.22. 若抛物线L:y=ax2+bx+c(a,b,c是常数,abc≠0)与直线l都经过y轴上的一点P,且抛物线L的顶点Q在直线l上,则称此直线l与该抛物线L具有“一带一路”关系.此时,直线l叫做抛物线L的“带线”,抛物线L叫做直线l的“路线”.(1)、若直线y=mx+1与抛物线y=x2﹣2x+n具有“一带一路”关系,求m,n的值;(2)、若某“路线”L的顶点在反比例函数y= 的图象上,它的“带线”l的解析式为y=2x﹣4,求此“路线”L的解析式;(3)、当常数k满足 ≤k≤2时,求抛物线L:y=ax2+(3k2﹣2k+1)x+k的“带线”l与x轴,y轴所围成的三角形面积的取值范围.23. 课题:两个重叠的正多边形,其中的一个绕某一顶点旋转所形成的有关问题.实验与论证:
设旋转角∠A1A0B1=α(α<∠A1A0A2),θ3、θ4、θ5、θ6所表示的角如图所示.
 (1)、用含α的式子表示角的度数:θ3= , θ4= , θ5=;(2)、图1﹣图4中,连接A0H时,在不添加其他辅助线的情况下,是否存在与直线A0H垂直且被它平分的线段?若存在,请选择其中的一个图给出证明;若不存在,请说明理由;
(1)、用含α的式子表示角的度数:θ3= , θ4= , θ5=;(2)、图1﹣图4中,连接A0H时,在不添加其他辅助线的情况下,是否存在与直线A0H垂直且被它平分的线段?若存在,请选择其中的一个图给出证明;若不存在,请说明理由;归纳与猜想:
设正n边形A0A1A2…An﹣1与正n边形A0B1B2…Bn﹣1重合(其中,A1与B1重合),现将正多边形A0B1B2…Bn﹣1绕顶点A0逆时针旋转α(0°<α< °);
(3)、设θn与上述“θ3、θ4、…”的意义一样,请直接写出θn的度数;(4)、试猜想在正n边形的情形下,是否存在与直线A0H垂直且被它平分的线段?若存在,请将这条线段用相应的顶点字母表示出来(不要求证明);若不存在,请说明理由.