江西省赣州市2019年中考数学三模考试试卷
试卷更新日期：2020-04-26 类型：中考模拟
一、单选题
-
1. - 的相反数是（ ）A、2016 B、﹣2016 C、 D、-2. 下列判断不正确是（ ）A、两组对边分别相等的四边形是平行四边形 B、四个内角都相等的四边形是矩形 C、两条对角线垂直且平分的四边形是正方形 D、四条边都相等的四边形是菱形3. 某气象台发现：在某段时间里，如果早晨下雨，那么晚上是晴天；如果晚上下雨，那么早晨是晴天，已知这段时间有9天下了雨，并且有6天晚上是晴天，7天早晨是晴天，则这一段时间有（ ）A、9天 B、11天 C、13天 D、22天4. 如图，在等腰Rt△ABC中，AC＝BC＝2 ，点P在以斜边AB为直径的半圆上，M为PC的中点.当点P沿半圆从点A运动至点B时，点M运动的路径长是（ ）
A、2 B、2 C、π D、 π5. 如图，在▱ABCD中，AB=12，AD=8，∠ABC的平分线交CD于点F，交AD的延长线于点E，CG⊥BE，垂足为G，若EF=2，则线段CG的长为（ ）
A、 B、4 C、2 D、6. 如图，圆O的半径为1，AD，BC是⊙O的两条互相垂直的直径，点P从点O出发（P点与O点不重合），沿O→C→D的路线运动，设AP=x，sin∠APB=y，那么y与x之间的关系图象大致是（ ）
A、
B、
C、
D、
二、填空题
-
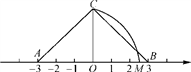
7. 已知|x﹣y+2|+ =0，则x2﹣y2的值为 ．8. 如图，O为数轴原点，A，B两点分别对应－3，3，作腰长为4的等腰△ABC，连接OC，以O为圆心，CO长为半径画弧交数轴于点M，则点M对应的实数为 ．
9. 已知不等式组 ，在同一条数轴上表示不等式①，②的解集如图所示，则b﹣a的值为 ．
10. 如图，在正方形纸片ABCD中，EF∥AD，M，N是线段EF的六等分点，若把该正方形纸片卷成一个圆柱，使点A与点D重合，此时，底面圆的直径为10cm，则圆柱上M，N两点间的距离是cm．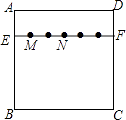
11. 如图，在四边形ABCD中，∠ABC＝90°，AB＝3，BC＝4，CD＝10，DA＝
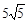，则BD的长为 ． 
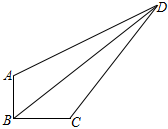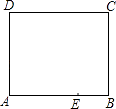
12.如图是一张长方形纸片ABCD，已知AB=8，AD=7，E为AB上一点，AE=5，现要剪下一张等腰三角形纸片（△AEP），使点P落在长方形ABCD的某一条边上，则等腰三角形AEP的底边长是 ．
三、解答题
-
13. 先化简，再求值： ，其中x＝ ，y＝ ．14.
如图，点O是△ABC内一点，连结OB、OC，并将AB、OB、OC、AC的中点D、E、F、G依次连结，得到四边形DEFG．
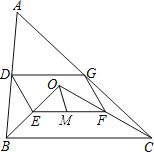(1)、求证：四边形DEFG是平行四边形；(2)、若M为EF的中点，OM=3，∠OBC和∠OCB互余，求DG的长度．15. 如图，△ABC是⊙O的内接三角形．∠BAC＝45°．请用无刻度的直尺按要求画图．
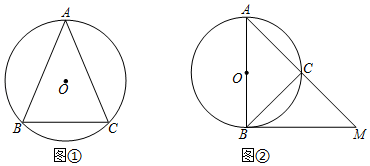(1)、如图①，请在图①中画出弦CD ， 使得CD＝BC；(2)、如图②，AB是⊙O的直径，BM是⊙O的切线，点A ， C ， M在同一条直线上．在图中画出△ABM的边BM上的中线AD ．16. 如图，在Rt△ABC中，∠A=90°．AB=8cm，AC=6cm，若动点D从B出发，沿线段BA运动到点A为止（不考虑D与B ， A重合的情况），运动速度为2cm/s，过点D作DE∥BC交AC于点E ， 连接BE ， 设动点D运动的时间为x（s），AE的长为y（cm）．
(1)、求y关于x的函数表达式，并写出自变量x的取值范围；(2)、当x为何值时，△BDE的面积S有最大值？最大值为多少？17. 网上购物已经成为人们常用的一种购物方式，售后评价特别引人关注，消费者在网店购买某种商品后，对其有“好评”、“中评”、“差评”三种评价，假设这三种评价是等可能的．
(1)、小明对一家网店销售某种商品显示的评价信息进行了统计，并列出了两幅不完整的统计图．利用图中所提供的信息解决以下问题：
①小明一共统计了个评价；
②请将图1补充完整；
③图2中“差评”所占的百分比是；
(2)、若甲、乙两名消费者在该网店购买了同一商品，请你用列表格或画树状图的方法帮助店主求一下两人中至少有一个给“好评”的概率．18. 如图，AB是⊙O的直径，点C、D在⊙O上，∠A=2∠BCD，点E在AB的延长线上，∠AED=∠ABC
(1)、求证：DE与⊙O相切；(2)、若BF=2，DF= ，求⊙O的半径．19. 如图，在平面直角坐标系中，点A、B分别在x轴、y轴的正半轴上，OA=4，AB=5，点D在反比例函数 （k>0）的图象上， ，点P在y轴负半轴上，OP=7.
(1)、求点B的坐标和线段PB的长；(2)、当 时，求反比例函数的解析式．20. 甲、乙两人利用扑克牌玩“10点”游戏，游戏规则如下：①将牌面数字作为“点数”，如红桃6的“点数”就是6（牌面点数与牌的花色无关）；
②两人摸牌结束时，将所得牌的“点数”相加，若“点数”之和小于或等于10，此时“点数”之和就是“最终点数”，若“点数”之和大于10，则“最终点数”是0；
③游戏结束之前双方均不知道对方“点数”；
④判定游戏结果的依据是：“最终点数”大的一方获胜，“最终点数”相等时不分胜负．
现甲、乙均各自摸了两张牌，数字之和都是5，这时桌上还有四张背面朝上的扑克牌，牌面数字分别是4，5，6，7．
(1)、若甲从桌上继续摸一张扑克牌，乙不再摸牌，则甲获胜的概率为；(2)、若甲先从桌上继续摸一张扑克牌，接着乙从剩下的扑克牌中摸出一张牌，然后双方不再摸牌，请用树状图或表格表示出这次摸牌后所有可能的结果，再列表呈现甲、乙的“最终点数”，并求乙获胜的概率．21. 如图，已知四边形ABCD和四边形DEFG为正方形，点E在线段DC上，点A ， D ， G在同一直线上，且AD＝3，DE＝1，连接AC ， CG ， AE ， 并延长AE交CG于点H.
(1)、求sin∠EAC的值；(2)、求线段AH的长．22. 小杰到学校食堂买饭，看到A、B两窗口前面排队的人一样多(设为a人，a＞8），就站在A窗口队伍的后面，过了2分钟，他发现A窗口每分钟有4人买了饭离开队伍，B窗口每分钟有6人买了饭离开队伍，且B窗口队伍后面每分钟增加5人．
(1)、此时，若小杰继续在A窗口排队，则他到达窗口所花的时间是多少；（用含a的代数式表示）(2)、此时，若小杰迅速从A窗口队伍转移到B窗口后面重新排队，且到达B窗口所花的时间比继续在A窗口排队到达A窗口所花的时间少，求a的取值范围．（不考虑其它因素）23. 如图1，已知平行四边形ABCD顶点A的坐标为（2，6），点B在y轴上，且AD∥ BC∥ x轴，过B，C，D三点的抛物线y=ax2+bx+c（a≠0）的顶点坐标为（2，2），点F（m，6）是线段AD上一动点，直线OF交BC于点E．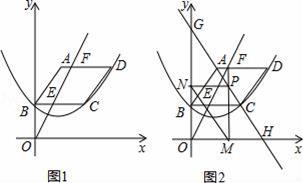
(1)、求抛物线的表达式；(2)、设四边形ABEF的面积为S，请求出S与m的函数关系式，并写出自变量m的取值范围；(3)、如图2，过点F作FM⊥x轴，垂足为M，交直线AC于P，过点P作PN⊥y轴，垂足为N，连接MN，直线AC分别交x轴，y轴于点H，G，试求线段MN的最小值，并直接写出此时m的值．