江西省赣州市2019年中考数学二模考试试卷

试卷更新日期：2020-04-26 类型：中考模拟

进入出卷网下载

一、单选题

1. －6的绝对值是（）

A、-6 B、6 C、- $\frac{1}{6}$ D、 $\frac{1}{6}$

查看试题解析
2. 如图，数轴上点P对应的数为p，则数轴上与数﹣ $\frac{p}{2}$ 对应的点是（）

A、点A B、点B C、点C D、点D

查看试题解析
3. 若x>y ，则下列不等式不一定成立的是（）

A、x＋1>y＋1 B、2x>2y C、 $\frac{x}{2}$ > $\frac{y}{2}$ D、x²>y²

查看试题解析
4. 已知△ABC中，BC=6，AC=3，CP⊥AB，垂足为P，则CP的长可能是（）

A、2 B、4 C、5 D、7

查看试题解析
5. 如图，MN是⊙O的直径，MN=2，点A在⊙O上，∠AMN=30°，B为 $\overset{⌢}{A N}$ 的中点，P是直径MN上一动点，则PA+PB的最小值为（）

A、 $2 \sqrt{2}$ B、 $\sqrt{2}$ C、1 D、2

查看试题解析
6. 已知反比例函数y= $\frac{k}{x}$ 的图象如图，则二次函数y=2kx²-4x+k²的图象大致为（）

A、 B、 C、 D、

查看试题解析

二、填空题

7. 若点A在第二象限，且到x轴的距离为3，到y轴的距离为2，则点A的坐标为．

查看试题解析
8. 如图，AC经过⊙O的圆心O ， AB与⊙O相切于点B ，若∠A＝50°，则∠C＝度．

查看试题解析
9. 已知（m-n）²=8，(m+n)²=2，则m²+n²=.

查看试题解析
10. 小芳随机地向如图所示的圆形簸箕内撒了几把豆子，则豆子落到圆内接正方形(阴影部分)区域的概率是．

查看试题解析
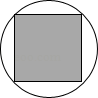11. 若一个一元二次方程的两个根分别是Rt△ABC的两条直角边长，且S_△ABC=3，请写出一个正确一元二次方程．

查看试题解析
12.
如图，在△ABC中，AB=BC=4，AO=BO，P是射线CO上的一个动点，∠AOC=60°，则当△PAB为直角三角形时，AP的长为

查看试题解析

三、解答题

13. 计算： $| \sqrt{3} - 1 | - 4^{\frac{1}{2}} - \sqrt{12} + {(\frac{1}{3})}^{- 2}$ ．

查看试题解析
14. 化简： $(x - 5 + \frac{16}{x + 3}) \div \frac{x - 1}{x^{2} - 9}$ ．

查看试题解析
15. 如图，已知多边形ABCDEF中，AB＝AF ， DC＝DE ， BC＝EF ， ∠ABC＝∠BCD ．请仅用无刻度的直尺，分别按下列要求画图．

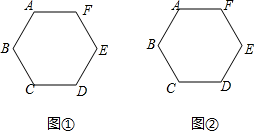(1)、在图①中，画出一个以BC为边的矩形；

(2)、在图②中，若多边形ABCDEF是正六边形，试在AF上画出点M ，使得AM＝ $\frac{1}{4}$ AF ．

查看试题解析
16. 在平面直角坐标系中，一次函数 $y = a x + b$ （a≠0）的图象与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象交于第二、第四象限内的A、B两点，与 $y$ 轴交于点C，过点A作AH⊥ $y$ 轴，垂足为点H，OH=3，tan∠AOH= $\frac{4}{3}$ ，点B的坐标为（ $m$ ，-2）.

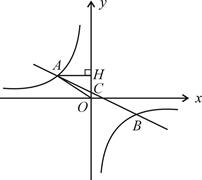(1)、求该反比例函数和一次函数的解析式；

(2)、求△AHO的周长.

查看试题解析
17. 为了解某小区某月家庭用水量的情况，从该小区随机抽取部分家庭进行调查，以下是根据调查数据绘制的统计图表的一部分
分组
家庭用水量x/吨
家庭数/户
A
0≤x≤4.0
4
B
4.0＜x≤6.5
13
C
6.5＜x≤9.0
D
9.0＜x≤11.5
E
11.5＜x≤14.0
6
F
x＞4.0
3
根据以上信息，解答下列问题

(1)、家庭用水量在4.0＜x≤6.5范围内的家庭有户，在6.5＜x≤9.0范围内的家庭数占被调查家庭数的百分比是%；

(2)、本次调查的家庭数为户，家庭用水量在9.0＜x≤11.5范围内的家庭数占被调查家庭数的百分比是%；

(3)、家庭用水量的中位数落在组；

(4)、若该小区共有200户家庭，请估计该月用水量不超过9.0吨的家庭数．

查看试题解析
18. 如图，AB是⊙O的直径，点C、D在⊙O上，∠A=2∠BCD，点E在AB的延长线上，∠AED=∠ABC

(1)、求证：DE与⊙O相切；

(2)、若BF=2，DF= $\sqrt{10}$ ，求⊙O的半径．

查看试题解析
19.
某教室的开关控制板上有四个外形完全相同的开关，其中两个分别控制A、B两盏电灯，另两个分别控制C、D两个吊扇．已知电灯、吊扇均正常，且处于不工作状态，开关与电灯、电扇的对应关系未知．

(1)、若四个开关均正常，则任意按下一个开关，正好一盏灯亮的概率是多少？

(2)、若其中一个控制电灯的开关坏了，则任意按下两个开关，正好一盏灯亮和一个扇转的概率是多少？请用树状图法或列表法加以说明．

查看试题解析
20. 图中是抛物线拱桥，P处有一照明灯，水面OA宽4m ，从O、A两处观测P处，仰角分别为α、β，且tanα＝ $\frac{1}{2}$ ，tanβ＝ $\frac{3}{2}$ ，以O为原点，OA所在直线为x轴建立直角坐标系．

(1)、求点P的坐标；

(2)、水面上升1m ，水面宽多少？

查看试题解析
21.
如图1，△ABC中，∠C=90°，线段DE在射线BC上，且DE=AC，线段DE沿射线BC运动，开始时，点D与点B重合，点D到达点C时运动停止，过点D作DF=DB，与射线BA相交于点F，过点E作BC的垂线，与射线BA相交于点G．设BD=x，四边形DEGF与△ABC重叠部分的面积为S，S关于x的函数图象如图2所示（其中0＜x≤m，1＜x≤m，m＜x≤3时，函数的解析式不同）

(1)、填空：BC的长是；

(2)、求S关于x的函数关系式，并写出x的取值范围．

查看试题解析
22. 如图1，边长为4的正方形ABCD中，点E在AB边上(不与点A ， B重合)，点F在BC边上(不与点B、C重合)．
第一次操作：将线段EF绕点F顺时针旋转，当点E落在正方形上时，记为点G；

第二次操作：将线段FG绕点G顺时针旋转，当点F落在正方形上时，记为点H；

依此操作下去…

(1)、图2中的△EFD是经过两次操作后得到的，其形状为，求此时线段EF的长；

(2)、若经过三次操作可得到四边形EFGH ．
请判断四边形EFGH的形状为，此时AE与BF的数量关系是；

(3)、以①中的结论为前提，设AE的长为x ，四边形EFGH的面积为y ，求y与x的函数关系式及面积y的取值范围．

查看试题解析
23. 如图1，A ， B分别在射线OM ， ON上，且∠MON为钝角，现以线段OA ， OB为斜边向∠MON的外侧作等腰直角三角形，分别是△OAP ， △OBQ ，点C ， D ， E分别是OA ， OB ， AB的中点．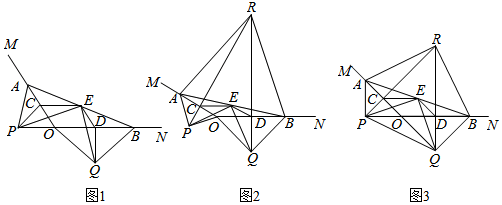

(1)、求证：△PCE≌△EDQ；

(2)、延长PC ， QD交于点R ．
①如图2，若∠MON＝150°，求证：△ABR为等边三角形；

②如图3，若△ARB∽△PEQ ，求∠MON大小和 $\frac{AB}{PQ}$ 的值．

查看试题解析

分组	家庭用水量x/吨	家庭数/户
A	0≤x≤4.0	4
B	4.0＜x≤6.5	13
C	6.5＜x≤9.0
D	9.0＜x≤11.5
E	11.5＜x≤14.0	6
F	x＞4.0	3