江西省赣州市2019年中考数学3月模拟考试试卷
试卷更新日期:2020-04-26 类型:中考模拟
一、单选题
-
1. 已知关于x的不等式3x﹣m+1>0的最小整数解为2,则实数m的取值范围是( )
A、4≤m<7 B、4<m<7 C、4≤m≤7 D、4<m≤72. 如图,点A,B在反比例函数 的图象上,点C,D在反比例函数 的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为 ,则k的值为( )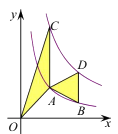 A、4 B、3 C、2 D、3. 坐标平面上有一个轴对称图形, 、 两点在此图形上且互为对称点.若此图形上有一点C(﹣2,﹣9),则C的对称点坐标为何( )A、(﹣2,1) B、 C、 D、(8,﹣9)4. 若函数 ,则当自变量 取1、2、3、…、100这100个自然数时,函数值的和是( )。A、540 B、390 C、194 D、975. 现有7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
A、4 B、3 C、2 D、3. 坐标平面上有一个轴对称图形, 、 两点在此图形上且互为对称点.若此图形上有一点C(﹣2,﹣9),则C的对称点坐标为何( )A、(﹣2,1) B、 C、 D、(8,﹣9)4. 若函数 ,则当自变量 取1、2、3、…、100这100个自然数时,函数值的和是( )。A、540 B、390 C、194 D、975. 现有7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )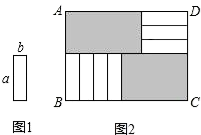 A、a=2b B、a=3b C、a=3.5b D、a=4b6. 如图①,在矩形 ABCD 中,动点 E 从点 A 出发,沿 AB→BC 方向运动,当点 E 到达点 C 时 停止运动.过点 E 作 FE⊥AE,交 CD 于 F 点,设点 E 运动路程为 x,FC=y,图②表示 y与 x 的函数关系的大致图像,则矩形 ABCD 的面积是( )
A、a=2b B、a=3b C、a=3.5b D、a=4b6. 如图①,在矩形 ABCD 中,动点 E 从点 A 出发,沿 AB→BC 方向运动,当点 E 到达点 C 时 停止运动.过点 E 作 FE⊥AE,交 CD 于 F 点,设点 E 运动路程为 x,FC=y,图②表示 y与 x 的函数关系的大致图像,则矩形 ABCD 的面积是( )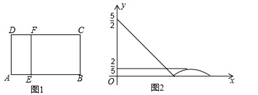 A、 B、5 C、6 D、
A、 B、5 C、6 D、二、填空题
-
7. a、b为实数,且ab=1,设P= ,Q= ,则PQ(填“>”、“<”或“=”).
8. 如图,在菱形ABCD和菱形BEFG中,点A、B、E在同一直线上,P是线段DF的中点,连接PG , PC . 若∠ABC=∠BEF=60°,则 = .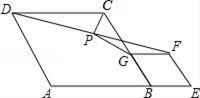 9. 设 是一列正整数,其中 表示第一个数, 表示第二个数,依此类推, 表示第 个数( 是正整数),已知 , ,则 .10. 高斯函数 ,也称为取整函数,即 表示不超过 的最大整数.
9. 设 是一列正整数,其中 表示第一个数, 表示第二个数,依此类推, 表示第 个数( 是正整数),已知 , ,则 .10. 高斯函数 ,也称为取整函数,即 表示不超过 的最大整数.例如: , .
则下列结论:
① ;
② ;
若 ,则 的取值范围是 ;
当 时, 的值为 、 、 .
其中正确结论有(写出所有正确结论的序号).
11. 关于x的一元二次方程 的两个不相等的实数根都在-1和0之间(不包括-1和0),则a的取值范围是12. 矩形ABCD中,对角线AC、BD交于点O, 于 ,若 , ,则 .三、解答题
-
13. 已知抛物线 (b是常数)经过点A(-1,0).(1)、求该抛物线的解析式和顶点坐标;(2)、P(m,t)为抛物线上的一个动点,P关于原点的对称点为 .
①当点 落在该抛物线上时,求m的值;
②当点 落在第二象限内, A2取得最小值时,求m的值.
14. 如图1,以点M(-1,0)为圆心的圆与y轴、x轴分别交于点A、B、C、D,直线y=- x- 与⊙M相切于点H,交x轴于点E,交y轴于点F.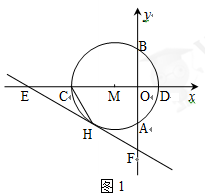

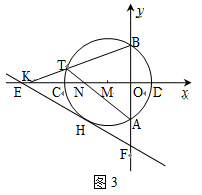 (1)、请直接写出OE、⊙M的半径r、CH的长;(2)、如图2,弦HQ交x轴于点P,且DP : PH=3 : 2,求cos∠QHC的值;(3)、如图3,点K为线段EC上一动点(不与E、C重合),连接BK交⊙M于点T,弦AT交x轴于点N.是否存在一个常数a , 始终满足MN·MK=a , 如果存在,请求出a的值;如果不存在,请说明理由.15. 如图,在四边形ABCD中,∠B=60°,∠D=30°,AB=BC.
(1)、请直接写出OE、⊙M的半径r、CH的长;(2)、如图2,弦HQ交x轴于点P,且DP : PH=3 : 2,求cos∠QHC的值;(3)、如图3,点K为线段EC上一动点(不与E、C重合),连接BK交⊙M于点T,弦AT交x轴于点N.是否存在一个常数a , 始终满足MN·MK=a , 如果存在,请求出a的值;如果不存在,请说明理由.15. 如图,在四边形ABCD中,∠B=60°,∠D=30°,AB=BC.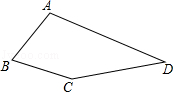 (1)、求∠A+∠C的度数;(2)、连接BD,探究AD,BD,CD三者之间的数量关系,并说明理由;(3)、若AB=1,点E在四边形ABCD内部运动,且满足AE2=BE2+CE2 , 求点E运动路径的长度.16. 如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”.
(1)、求∠A+∠C的度数;(2)、连接BD,探究AD,BD,CD三者之间的数量关系,并说明理由;(3)、若AB=1,点E在四边形ABCD内部运动,且满足AE2=BE2+CE2 , 求点E运动路径的长度.16. 如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”. (1)、若△ABC是“准互余三角形”,∠C>90°,∠A=60°,则∠B=°;(2)、如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5.若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.(3)、如图②,在四边形ABCD中,AB=7,CD=12,BD⊥CD,∠ABD=2∠BCD,且△ABC是“准互余三角形”,求对角线AC的长.
(1)、若△ABC是“准互余三角形”,∠C>90°,∠A=60°,则∠B=°;(2)、如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5.若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.(3)、如图②,在四边形ABCD中,AB=7,CD=12,BD⊥CD,∠ABD=2∠BCD,且△ABC是“准互余三角形”,求对角线AC的长.