江西省赣州市信丰县2019年中考数学模拟考试试卷
试卷更新日期:2020-04-26 类型:中考模拟
一、单选题
-
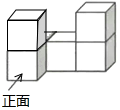
1. 计算 的结果是( )A、 B、 C、 D、2. 如图是由6个大小相同的小正方体搭成的几何体,这个几何体的左视图是( )
 A、
A、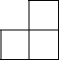 B、
B、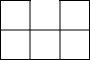 C、
C、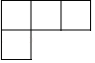 D、
D、 3. 是一名同学做的6道练习题:①(﹣3)0=1;②a3+a3=a6;③(﹣a5)÷(﹣a3)=﹣a2;④4m﹣2= ;⑤(xy2)3=x3y6;⑥22+23=25 , 其中做对的题有( )A、1道 B、2道 C、3道 D、4道4. 甲、乙两地去年 12 月前 5 天的日平均气温如图所示,下列描述不正确是( )
3. 是一名同学做的6道练习题:①(﹣3)0=1;②a3+a3=a6;③(﹣a5)÷(﹣a3)=﹣a2;④4m﹣2= ;⑤(xy2)3=x3y6;⑥22+23=25 , 其中做对的题有( )A、1道 B、2道 C、3道 D、4道4. 甲、乙两地去年 12 月前 5 天的日平均气温如图所示,下列描述不正确是( ) A、甲地气温的中位数是 6℃ B、两地气温的平均数相同 C、乙地气温的众数是 8℃ D、乙地气温相对比较稳定5. 分式方程 有增根,则 的值为( )A、0和3 B、1 C、1和 D、36. 如图,AC是⊙O的直径,∠A=30°,BD是⊙O的切线,C为切点,AB与⊙O相交于点E , OC=CD , BC=2,OD与⊙O相交于点F , 则弧EF的长为( )
A、甲地气温的中位数是 6℃ B、两地气温的平均数相同 C、乙地气温的众数是 8℃ D、乙地气温相对比较稳定5. 分式方程 有增根,则 的值为( )A、0和3 B、1 C、1和 D、36. 如图,AC是⊙O的直径,∠A=30°,BD是⊙O的切线,C为切点,AB与⊙O相交于点E , OC=CD , BC=2,OD与⊙O相交于点F , 则弧EF的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 一个正数a的平方根分别是2m﹣1和﹣3m+ ,则这个正数a为 .8. 分解因式:3x3﹣27x= .9. 在平行四边形ABCD中,E , F分别是AD、CD的中点,线段BA、BC的延长线与直线EF分别交于点G、H , 若S△DEF=1,则五边形ABCFE的面积是 .
 10. 如图,正六边形的面积为6a , 则图中阴影部分的面积为 .
10. 如图,正六边形的面积为6a , 则图中阴影部分的面积为 . 11. 若方程2x2+x﹣2m+1=0有一正实根和一负实根,则m的取值范围是 .12. 已知一次函数 的图象上两点 、 ,当 时,有 ,并且图象不经过第三象限,则a的取值范围是 .
11. 若方程2x2+x﹣2m+1=0有一正实根和一负实根,则m的取值范围是 .12. 已知一次函数 的图象上两点 、 ,当 时,有 ,并且图象不经过第三象限,则a的取值范围是 .三、解答题
-
13. 计算:2sin30°﹣tan45°+sin229°+cos229°14. 如图,三张“黑桃”扑克牌,背面完全相同将三张扑克牌背面朝上,洗匀后放在桌面上甲,乙两人进行摸牌游戏,甲先从中随机抽取一张,记下数字再放回洗匀,乙再从中随机抽取一张.
 (1)、甲抽到“黑桃”,这一事件是事件(填“不可能“,“随机“,“必然”);(2)、利用树状图或列表的方法,求甲乙两人抽到同一张扑克牌的概率.15. 解不等式组: ,并把解集在数轴上表示出来.
(1)、甲抽到“黑桃”,这一事件是事件(填“不可能“,“随机“,“必然”);(2)、利用树状图或列表的方法,求甲乙两人抽到同一张扑克牌的概率.15. 解不等式组: ,并把解集在数轴上表示出来.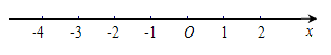 16. 在数学课上,老师提出利用尺规作图完成下面问题:已知:△ABC是⊙O的内接三角形.求作:△ABC中∠BAC的平分线.
16. 在数学课上,老师提出利用尺规作图完成下面问题:已知:△ABC是⊙O的内接三角形.求作:△ABC中∠BAC的平分线.
小明的作法如下:
(1)、作BC边的垂直平分线DE , 交BC于点D , 交弧BC于点E;(2)、连接AE , 交BC边于点F;则线段AF为所求△ABC中∠BAC的平分线.根据小明设计的尺规作图过程,①在图中补全图形(尺规作图,保留作图痕迹);
②完成下面的证明.
证明:∵OB=OC , DE是线段BC的垂直平分线
∴圆心O在直线DE上().
∵DE⊥BC ,
∴ ().
∴∠BAE=∠CAE(),
∴线段AF为所求△ABC中∠BAC的平分线.
17. 某旅游团于早上8:00从某旅行社出发,乘大巴车前往“珠海长隆”旅游,“珠海长隆”离该旅行社有100千米,导游张某因有事情,于8:30从该旅行社自驾小车以大巴1.5倍的速度追赶,追上大巴后继续前行,结果比该旅游团提前20分钟到达“珠海长隆”.(1)、大巴与小车的平均速度各是多少?(2)、导游张某追上大巴的地点到“珠海长隆”的路程有多远?18. “世界读书日”前夕,某校开展了“读书助我成长”的阅读活动.为了了解该校学生在此次活动中课外阅读书籍的数量情况,随机抽取了部分学生进行调查,将收集到的数据进行整理,绘制出两幅不完整的统计图,请根据统计图信息解决下列问题: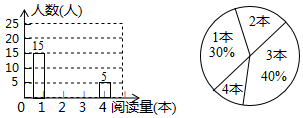 (1)、求本次调查中共抽取的学生人数;(2)、补全条形统计图;(3)、在扇形统计图中,阅读 本书籍的人数所在扇形的圆心角度数是;(4)、若该校有 名学生,估计该校在这次活动中阅读书籍的数量不低于 本的学生有多少人?19. 如图,一辆摩拜单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A、B之间的距离约为49cm,现测得AC、BC与AB的夹角分别为45°与68°,若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为4cm,求点E到地面的距离(结果保留一位小数).(参考数据:sin68°≈0.93,cos68°≈0.37,cot68°≈0.40)
(1)、求本次调查中共抽取的学生人数;(2)、补全条形统计图;(3)、在扇形统计图中,阅读 本书籍的人数所在扇形的圆心角度数是;(4)、若该校有 名学生,估计该校在这次活动中阅读书籍的数量不低于 本的学生有多少人?19. 如图,一辆摩拜单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A、B之间的距离约为49cm,现测得AC、BC与AB的夹角分别为45°与68°,若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为4cm,求点E到地面的距离(结果保留一位小数).(参考数据:sin68°≈0.93,cos68°≈0.37,cot68°≈0.40)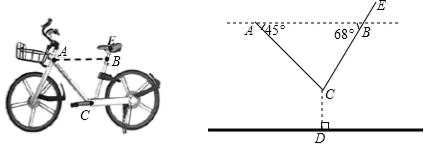 20. 如图,直线y=2x+2与y轴交于A点,与反比例函数y= (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
20. 如图,直线y=2x+2与y轴交于A点,与反比例函数y= (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2. (1)、求H点的坐标及k的值;(2)、点P在y轴上,使△AMP是以AM为腰的等腰三角形,请直接写出所有满足条件的P点坐标;(3)、点N(a,1)是反比例函数y= (x>0)图象上的点,点Q(m,0)是x轴上的动点,当△MNQ的面积为3时,请求出所有满足条件的m的值.21. 已知如图,△ABC中AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B、M两点的⊙O交BC于G,交AB于点F,FB恰为⊙O的直径.
(1)、求H点的坐标及k的值;(2)、点P在y轴上,使△AMP是以AM为腰的等腰三角形,请直接写出所有满足条件的P点坐标;(3)、点N(a,1)是反比例函数y= (x>0)图象上的点,点Q(m,0)是x轴上的动点,当△MNQ的面积为3时,请求出所有满足条件的m的值.21. 已知如图,△ABC中AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B、M两点的⊙O交BC于G,交AB于点F,FB恰为⊙O的直径. (1)、求证:AE与⊙O相切;(2)、当BC=6,cosC= ,求⊙O的直径.22. 如图,直线AB和抛物线的交点是A(0,﹣3),B(5,9),已知抛物线的顶点D的横坐标是2.
(1)、求证:AE与⊙O相切;(2)、当BC=6,cosC= ,求⊙O的直径.22. 如图,直线AB和抛物线的交点是A(0,﹣3),B(5,9),已知抛物线的顶点D的横坐标是2.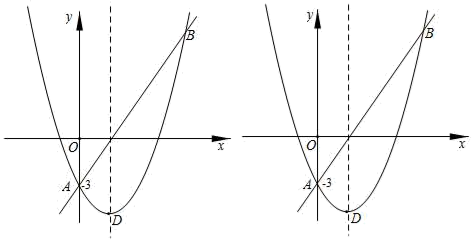 (1)、求抛物线的解析式及顶点坐标;(2)、在x轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不在,请说明理由;(3)、在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.23. 如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)、求抛物线的解析式及顶点坐标;(2)、在x轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不在,请说明理由;(3)、在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.23. 如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.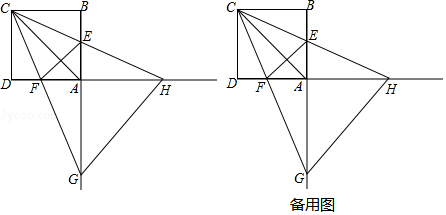 (1)、填空:∠AHC∠ACG;(填“>”或“<”或“=”)(2)、线段AC,AG,AH什么关系?请说明理由;(3)、设AE=m,
(1)、填空:∠AHC∠ACG;(填“>”或“<”或“=”)(2)、线段AC,AG,AH什么关系?请说明理由;(3)、设AE=m,①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.