江西省宜春市2019年中考数学4月模拟考试试卷
试卷更新日期:2020-04-26 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 目前,世界上能制造出的最小晶体管的长度只有0.00000004m,将0.00000004用科学记数法表示为( )A、0.4×108 B、4×108 C、4×10﹣8 D、﹣4×1083. 下列图形中,是中心对称图形但不是轴对称图形的是( )A、
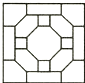 B、
B、 C、
C、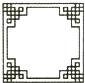 D、
D、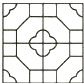 4. 已知一元二次方程x2+x﹣1=0,下列判断正确是( )A、该方程有两个相等的实数根 B、该方程有一个根为1 C、该方程没有实数根 D、该方程有一个根为负数5. 如图,在△ABC中,AC=BC,有一动点P从点A出发,沿A→C→B→A匀速运动,则CP的长度s与时间t之间的函数关系用图象描述大致是( )
4. 已知一元二次方程x2+x﹣1=0,下列判断正确是( )A、该方程有两个相等的实数根 B、该方程有一个根为1 C、该方程没有实数根 D、该方程有一个根为负数5. 如图,在△ABC中,AC=BC,有一动点P从点A出发,沿A→C→B→A匀速运动,则CP的长度s与时间t之间的函数关系用图象描述大致是( )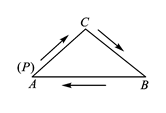 A、
A、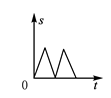 B、
B、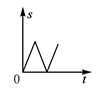 C、
C、 D、
D、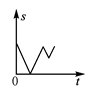 6. 如图,正方形ABCD中,E为AB中点,FE⊥AB,AF=2AE,FC交BD于O,则∠DOC的度数为( )
6. 如图,正方形ABCD中,E为AB中点,FE⊥AB,AF=2AE,FC交BD于O,则∠DOC的度数为( )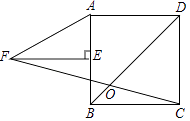 A、60° B、67.5° C、75° D、54°
A、60° B、67.5° C、75° D、54°二、填空题
-
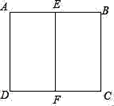
7. 分解因式:3x2﹣9= .8. 数据1,0,5,3,5,π,4的中位数是 .9. 从某一个方向观察一个正六棱柱,可看到如图所示的图形,其中四边形ABCD为矩形,E、F分别是AB、DC的中点,若AD=8,AB=6,则这个正六棱柱的侧面积为 .
 10. 不等式组 的整数解为 .11. 已知如图,矩形OCBD如图所示,OD=2,OC=3,反比例函数的图象经过点B,点A为第一象限双曲线上的动点(点A的横坐标大于2),过点A作AF⊥BD于点F,AE⊥x轴于点E,连接OB,AD,若△OBD∽△DAE,则点A的坐标是 .
10. 不等式组 的整数解为 .11. 已知如图,矩形OCBD如图所示,OD=2,OC=3,反比例函数的图象经过点B,点A为第一象限双曲线上的动点(点A的横坐标大于2),过点A作AF⊥BD于点F,AE⊥x轴于点E,连接OB,AD,若△OBD∽△DAE,则点A的坐标是 . 12. 如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上,以AD为折痕将△ABD折叠得到△AB′D,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是 .
12. 如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上,以AD为折痕将△ABD折叠得到△AB′D,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是 .
三、解答题
-
13.(1)、解方程: ;(2)、如图,四边形ABCD的对角线AC、BD交于点O,已知O是AC的中点,AE=CF,DE∥BE,求证:△BOE≌△DOF.
 14. 我市某校组织爱心捐书活动,准备将一批捐赠的书打包寄往贫困地区,其中每包书的数目相等.第一次他们领来这批书的 ,结果打了16个包还多40本;第二次他们把剩下的书全部取来,连同第一次打包剩下的书一起,刚好又打了9个包,那么这批书共有多少本?15. 为落实“垃圾分类”,环保部门要求垃圾要按A,B,C,D四类分别装袋、投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料、废纸等可回收物,D类指出其他垃圾,小明、小亮各投放了一袋垃圾.(1)、直接写出小明投放的垃圾恰好是A类的概率;(2)、求小亮投放的垃圾与小明投放的垃圾是同一类的概率.16. 如图,下列正方形网格的每个小正方形的边长均为1,⊙O的半径为 ,规定:顶点既在圆上又是正方形格点的直角三角形称为“圆格三角形”,请按下列要求使用无刻度的直尺各画一个“圆格三角形”,(1)、一个锐角的正切值为
14. 我市某校组织爱心捐书活动,准备将一批捐赠的书打包寄往贫困地区,其中每包书的数目相等.第一次他们领来这批书的 ,结果打了16个包还多40本;第二次他们把剩下的书全部取来,连同第一次打包剩下的书一起,刚好又打了9个包,那么这批书共有多少本?15. 为落实“垃圾分类”,环保部门要求垃圾要按A,B,C,D四类分别装袋、投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料、废纸等可回收物,D类指出其他垃圾,小明、小亮各投放了一袋垃圾.(1)、直接写出小明投放的垃圾恰好是A类的概率;(2)、求小亮投放的垃圾与小明投放的垃圾是同一类的概率.16. 如图,下列正方形网格的每个小正方形的边长均为1,⊙O的半径为 ,规定:顶点既在圆上又是正方形格点的直角三角形称为“圆格三角形”,请按下列要求使用无刻度的直尺各画一个“圆格三角形”,(1)、一个锐角的正切值为 (2)、面积为8
(2)、面积为8 17. 如图,已知平行四边形OBDC的对角线相交于点E,其中O(0,0),B(3,4),C(m,0),反比例函数y= (k≠0)的图象经过点B.
17. 如图,已知平行四边形OBDC的对角线相交于点E,其中O(0,0),B(3,4),C(m,0),反比例函数y= (k≠0)的图象经过点B. (1)、求反比例函数的解析式;(2)、若点E恰好落在反比例函数y= 上,求平行四边形OBDC的面积.18. 某中学现有学生2650人,学校为了进一步了解学生课余生活,组织调查各兴趣小组活动情况,为此校学生会进行了一次随机抽样调查,根据采集到的数据,绘制如下两个统计图(不完整)
(1)、求反比例函数的解析式;(2)、若点E恰好落在反比例函数y= 上,求平行四边形OBDC的面积.18. 某中学现有学生2650人,学校为了进一步了解学生课余生活,组织调查各兴趣小组活动情况,为此校学生会进行了一次随机抽样调查,根据采集到的数据,绘制如下两个统计图(不完整)
请你根据两个统计图中提供的信息,解答下列问题:
(1)、这次抽样调查的样本容量是多少?在图2中,请将条形统计图中的“体育”部分的图形补充完整;(2)、爱好“书画”的人数占被调查人数的百分数是多少?估计该中学现有的学生中,爱好“书画”的人数;(3)、求爱好“音乐”的人数对应扇形圆心角的度数.19. 一书架上的方格中放置四本厚度和长度相同的书,其中书架方格长BF=40cm,书的长度AB=20cm,设一本书的厚度为xcm. (1)、如图1左边三本书紧贴书架方格内侧竖放,右边一本书自然向左斜放,支撑点为C,E,最右侧书一个角正好靠在方格内侧上,若CG=4cm,求EF的长度;(2)、如图2左边两本书紧贴书架方格内侧竖放,右边两本书自然向左斜放,支撑点为C,E,最右侧书的下面两个角正好靠在方格内上,若∠DCE=30°,求x的值(保留一位小数).(参考数据: =1.414, =1.732)20. 如图1,点E为正方形ABCD的边AB上一点,EF⊥EC,且EF=EC,连接AF.
(1)、如图1左边三本书紧贴书架方格内侧竖放,右边一本书自然向左斜放,支撑点为C,E,最右侧书一个角正好靠在方格内侧上,若CG=4cm,求EF的长度;(2)、如图2左边两本书紧贴书架方格内侧竖放,右边两本书自然向左斜放,支撑点为C,E,最右侧书的下面两个角正好靠在方格内上,若∠DCE=30°,求x的值(保留一位小数).(参考数据: =1.414, =1.732)20. 如图1,点E为正方形ABCD的边AB上一点,EF⊥EC,且EF=EC,连接AF. (1)、求∠EAF的度数;(2)、如图2,连接FC交BD于M,交AD于N.求证:BD=AF+2DM.21. 如图,⊙A过▱OBCD的三顶点O、D、C,边OB与⊙A相切于点O,边BC与⊙O相交于点H,射线OA交边CD于点E,交⊙A于点F,点P在射线OA上,且∠PCD=2∠DOF,以O为原点,OP所在的直线为x轴建立平面直角坐标系,点B的坐标为(0,﹣2).
(1)、求∠EAF的度数;(2)、如图2,连接FC交BD于M,交AD于N.求证:BD=AF+2DM.21. 如图,⊙A过▱OBCD的三顶点O、D、C,边OB与⊙A相切于点O,边BC与⊙O相交于点H,射线OA交边CD于点E,交⊙A于点F,点P在射线OA上,且∠PCD=2∠DOF,以O为原点,OP所在的直线为x轴建立平面直角坐标系,点B的坐标为(0,﹣2). (1)、若∠BOH=30°,求点H的坐标;(2)、求证:直线PC是⊙A的切线;(3)、若OD= ,求⊙A的半径.22. 在四边形ABCD中,点E为AB边上的一点,点F为对角线BD上的一点,且EF⊥AB.
(1)、若∠BOH=30°,求点H的坐标;(2)、求证:直线PC是⊙A的切线;(3)、若OD= ,求⊙A的半径.22. 在四边形ABCD中,点E为AB边上的一点,点F为对角线BD上的一点,且EF⊥AB. (1)、若四边形ABCD为正方形.
(1)、若四边形ABCD为正方形.如图1,请直接写出AE与DF的数量关系;
(2)、将△EBF绕点B逆时针旋转到图2所示的位置,连接AE,DF,猜想AE与DF的数量关系并说明理由.(3)、若四边形ABCD为矩形,BC=mAB,其他条件都不变.①如图3,猜想AE与DF的数量关系并说明理由;
②将△EBF绕点B顺时针旋转α(0°<α<90°)得到△E′BF′,连接AE′,DF′,请在图4中画出草图,并直接写出AE′和DF′的数量关系.
23. 如图,抛物线y=ax2+2x与x轴相交于点B,其对称轴为x=3. (1)、求直线AB的解析式;(2)、过点O作直线l,使l∥AB,点P是l上一动点,设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为t,当0<S≤18时,求t的取值范围;(3)、在(2)的条件下,当t取最大值时,抛物线上是否存在点Q,使△OPQ为直角三角形且OP为直角边,若存在,求出点Q的坐标;若不存在,说明理由.
(1)、求直线AB的解析式;(2)、过点O作直线l,使l∥AB,点P是l上一动点,设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为t,当0<S≤18时,求t的取值范围;(3)、在(2)的条件下,当t取最大值时,抛物线上是否存在点Q,使△OPQ为直角三角形且OP为直角边,若存在,求出点Q的坐标;若不存在,说明理由.