江西省南昌市2019年中考数学三模考试试卷
试卷更新日期:2020-04-26 类型:中考模拟
一、单选题
-
1. 2018的倒数是( )A、﹣2018 B、 C、 D、20182. 人类生存的环境越来越受到人们的关注,某研究机构对空气进行了测量研究,发现在 0 摄氏度及一个标准大气压下 1cm3 空气的质量是 0.001293 克.数据0.001293 可用科学记数法表示为( )A、0.1293×10﹣2 B、1.293×10﹣3 C、12.93×10﹣4 D、0.1293×10﹣33. 计算正确是( )A、(﹣5)0=0 B、x3+x4=x7 C、(﹣a2b3)2=﹣a4b6 D、2a2•a﹣1=2a4. 下列图形中,已知∠1=∠2,则可得到 AB∥CD 的是( )A、
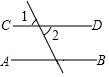 B、
B、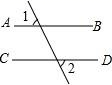 C、
C、 D、
D、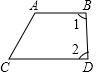 5. 如图是一个全封闭的物体,则它的俯视图是( )
5. 如图是一个全封闭的物体,则它的俯视图是( ) A、
A、 B、
B、 C、
C、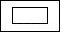 D、
D、 6.
6.如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )
 A、
A、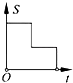 B、
B、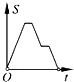 C、
C、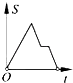 D、
D、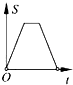
二、填空题
-
7. 若 x 的立方根是﹣2,则 x= .8. 为参加2018年“宜宾市初中毕业生升学体育考试”,小聪同学每天进行立定跳远练习,并记录下其中7天的最好成绩(单位:m)分别为:2.21,2.12,2.43,2.39,2.43,2.40,2.43.这组数据的中位数和众数分别是 .
9. 如图,⊙O 的直径 CD 垂直于弦 AB , ∠CAB=67.5°,则∠AOB=度.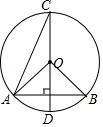 10. 已知 a、b 是方程 x2﹣2x﹣1=0 的两个根,则 a2﹣a+b 的值是 .11. 如图,点 A 是反比例函数 y=﹣ (x<0)图象上的点,分别过点 A 向横轴、纵轴作垂线段,与坐标轴恰好围成一个正方形,再以正方形的一组对边为直径作两个半圆,其余部分涂上阴影,则阴影部分的面积为 .
10. 已知 a、b 是方程 x2﹣2x﹣1=0 的两个根,则 a2﹣a+b 的值是 .11. 如图,点 A 是反比例函数 y=﹣ (x<0)图象上的点,分别过点 A 向横轴、纵轴作垂线段,与坐标轴恰好围成一个正方形,再以正方形的一组对边为直径作两个半圆,其余部分涂上阴影,则阴影部分的面积为 .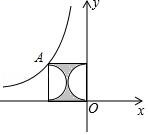 12. 如图,在平面直角坐标系中,O 为坐标原点,四边形 ABCD 是平行四边形,点 A、B、C 的坐标分别为 A(0,4),B(﹣2,0),C(8,0),点 E 是 BC的中点,点 P 为线段 AD 上的动点,若△BEP 是以 BE 为腰的等腰三角形,则点 P 的坐标为 .
12. 如图,在平面直角坐标系中,O 为坐标原点,四边形 ABCD 是平行四边形,点 A、B、C 的坐标分别为 A(0,4),B(﹣2,0),C(8,0),点 E 是 BC的中点,点 P 为线段 AD 上的动点,若△BEP 是以 BE 为腰的等腰三角形,则点 P 的坐标为 .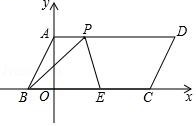
三、解答题
-
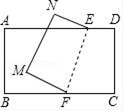
13.(1)、计算:﹣14﹣2×(﹣3)2+ ÷(﹣ )(2)、如图,小林将矩形纸片ABCD沿折痕EF翻折,使点C、D分别落在点M、N的位置,发现∠EFM=2∠BFM,求∠EFC的度数.
 14. 先化简,再求值: ÷(1﹣ ),其中 x= +1.15. 如图,AD 是⊙O 的直径,点 O 是圆心,C、F 是 AD 上的两点,OC=OF , B、E 是⊙O 上的两点,且 ,求证:BC∥EF .
14. 先化简,再求值: ÷(1﹣ ),其中 x= +1.15. 如图,AD 是⊙O 的直径,点 O 是圆心,C、F 是 AD 上的两点,OC=OF , B、E 是⊙O 上的两点,且 ,求证:BC∥EF .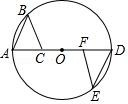 16. 请你仅用无刻度的直尺在下面的图中作出△ABC 的边 AB 上的高 CD.
16. 请你仅用无刻度的直尺在下面的图中作出△ABC 的边 AB 上的高 CD.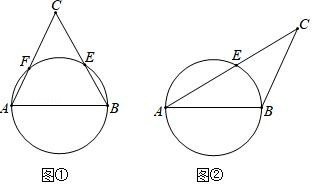 (1)、如图①,以等边三角形 ABC 的边 AB 为直径的圆,与另两边 BC、AC 分别交于点 E、F.(2)、如图②,以钝角三角形 ABC 的一短边 AB 为直径的圆,与最长的边 AC 相交于点 E.17. 已知某初级中学九(1)班共有40名同学,其中有22名男生,18名女生.(1)、若随机选一名同学,求选到男生的概率.(2)、学校因组织考试,将小明、小林随机编入A、B、C三个考场,请你用画树状图法或列表法求两人编入同一个考场的概率.18. 在我校举办的“读好书、讲礼仪”活动中,各班积极行动,图书角的新书、好书不断增多,除学校购买的图书外,还有师生捐献的图书,下面是九(1)班全体同学捐献图书情况的统计图(每人都有捐书).
(1)、如图①,以等边三角形 ABC 的边 AB 为直径的圆,与另两边 BC、AC 分别交于点 E、F.(2)、如图②,以钝角三角形 ABC 的一短边 AB 为直径的圆,与最长的边 AC 相交于点 E.17. 已知某初级中学九(1)班共有40名同学,其中有22名男生,18名女生.(1)、若随机选一名同学,求选到男生的概率.(2)、学校因组织考试,将小明、小林随机编入A、B、C三个考场,请你用画树状图法或列表法求两人编入同一个考场的概率.18. 在我校举办的“读好书、讲礼仪”活动中,各班积极行动,图书角的新书、好书不断增多,除学校购买的图书外,还有师生捐献的图书,下面是九(1)班全体同学捐献图书情况的统计图(每人都有捐书).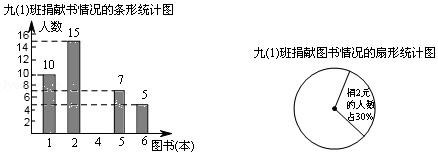
请你根据以上统计图中的信息,解答下列问题:
(1)、该班有学生多少人?(2)、补全条形统计图.(3)、九(1)班全体同学所捐图书是 6 本的人数在扇形统计图中所对应扇形的圆心角为多少度?(4)、请你估计全校 2000 名学生所捐图书的数量.19. 如图1,2分别是某款篮球架的实物图与示意图,已知底座BC的长为0.60m,底座BC与支架AC所成的角∠ACB=75°,点A、H、F在同一条直线上,支架AH段的长为1m,HF段的长为1.50m,篮板底部支架HE的长为0.75m.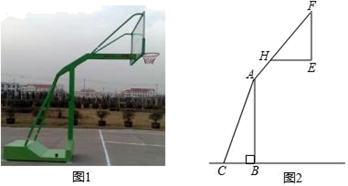 (1)、求篮板底部支架HE与支架AF所成的角∠FHE的度数.(2)、求篮板顶端F到地面的距离.(结果精确到0.1 m;参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732, ≈1.732, ≈1.414)20. 我市公交总公司为节约资源同时惠及民生,拟对一些乘客数量较少的路线投放“微型”公交车.该公司计划购买 10 台“微型”公交车,现有 A、B 两种型号,已知购买一台 A 型车比购买一台 B 型车多 20 万元,购买 2 台 A型车比购买 3 台 B 型车少 60 万元.(1)、问购买一台 A 型车和一台 B 型车分别需要多少万元?(2)、经了解,每台 A 型车每年节省 2.4 万元,每台 B 型车每年节省 2 万元,若购买这批公交车每年至少节省 22.4 万,则购买这批公交车至少需要多少万元?21. 如图,一次函数y=﹣x﹣2的图象与二次函数y=ax2+bx﹣4的图象交于x轴上一点A , 与y 轴交于点B , 在x轴上有一动点C . 已知二次函数y=ax2+bx﹣4的图象与y轴交于点D , 对称轴为直线x=n(n<0),n是方程2x2﹣3x﹣2=0的一个根,连接AD .
(1)、求篮板底部支架HE与支架AF所成的角∠FHE的度数.(2)、求篮板顶端F到地面的距离.(结果精确到0.1 m;参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732, ≈1.732, ≈1.414)20. 我市公交总公司为节约资源同时惠及民生,拟对一些乘客数量较少的路线投放“微型”公交车.该公司计划购买 10 台“微型”公交车,现有 A、B 两种型号,已知购买一台 A 型车比购买一台 B 型车多 20 万元,购买 2 台 A型车比购买 3 台 B 型车少 60 万元.(1)、问购买一台 A 型车和一台 B 型车分别需要多少万元?(2)、经了解,每台 A 型车每年节省 2.4 万元,每台 B 型车每年节省 2 万元,若购买这批公交车每年至少节省 22.4 万,则购买这批公交车至少需要多少万元?21. 如图,一次函数y=﹣x﹣2的图象与二次函数y=ax2+bx﹣4的图象交于x轴上一点A , 与y 轴交于点B , 在x轴上有一动点C . 已知二次函数y=ax2+bx﹣4的图象与y轴交于点D , 对称轴为直线x=n(n<0),n是方程2x2﹣3x﹣2=0的一个根,连接AD .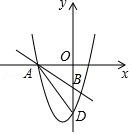 (1)、求二次函数的解析式.(2)、当S△ACB=3S△ADB 时,求点C的坐标.(3)、试判断坐标轴上是否存在这样的点C , 使得以点A、B、C组成的三角形与△ADB 相似?若存在,试求出点C的坐标;若不存在,请说明理由.22. 在学习了矩形这节内容之后,明明同学发现生活中的很多矩形都很特殊,如我们的课本封面、A4 的打印纸等,这些矩形的长与宽之比都为 :1,我们将具有这类特征的矩形称为“完美矩形”如图(1),在“完美矩形”ABCD 中,点 P 为 AB 边上的定点,且 AP=AD.
(1)、求二次函数的解析式.(2)、当S△ACB=3S△ADB 时,求点C的坐标.(3)、试判断坐标轴上是否存在这样的点C , 使得以点A、B、C组成的三角形与△ADB 相似?若存在,试求出点C的坐标;若不存在,请说明理由.22. 在学习了矩形这节内容之后,明明同学发现生活中的很多矩形都很特殊,如我们的课本封面、A4 的打印纸等,这些矩形的长与宽之比都为 :1,我们将具有这类特征的矩形称为“完美矩形”如图(1),在“完美矩形”ABCD 中,点 P 为 AB 边上的定点,且 AP=AD.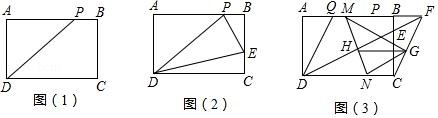 (1)、求证:PD=AB.(2)、如图(2),若在“完美矩形“ABCD 的边 BC 上有一动点 E,当 的值是多少时,△PDE 的周长最小?(3)、如图(3),点 Q 是边 AB 上的定点,且 BQ=BC.已知 AD=1,在(2)的条件下连接 DE 并延长交 AB 的延长线于点 F,连接 CF,G 为 CF 的中点,M、N 分别为线段 QF 和 CD 上的动点,且始终保持 QM=CN,MN 与 DF 相交于点 H,请问 GH 的长度是定值吗?若是,请求出它的值,若不是,请说明理由.
(1)、求证:PD=AB.(2)、如图(2),若在“完美矩形“ABCD 的边 BC 上有一动点 E,当 的值是多少时,△PDE 的周长最小?(3)、如图(3),点 Q 是边 AB 上的定点,且 BQ=BC.已知 AD=1,在(2)的条件下连接 DE 并延长交 AB 的延长线于点 F,连接 CF,G 为 CF 的中点,M、N 分别为线段 QF 和 CD 上的动点,且始终保持 QM=CN,MN 与 DF 相交于点 H,请问 GH 的长度是定值吗?若是,请求出它的值,若不是,请说明理由.